目录
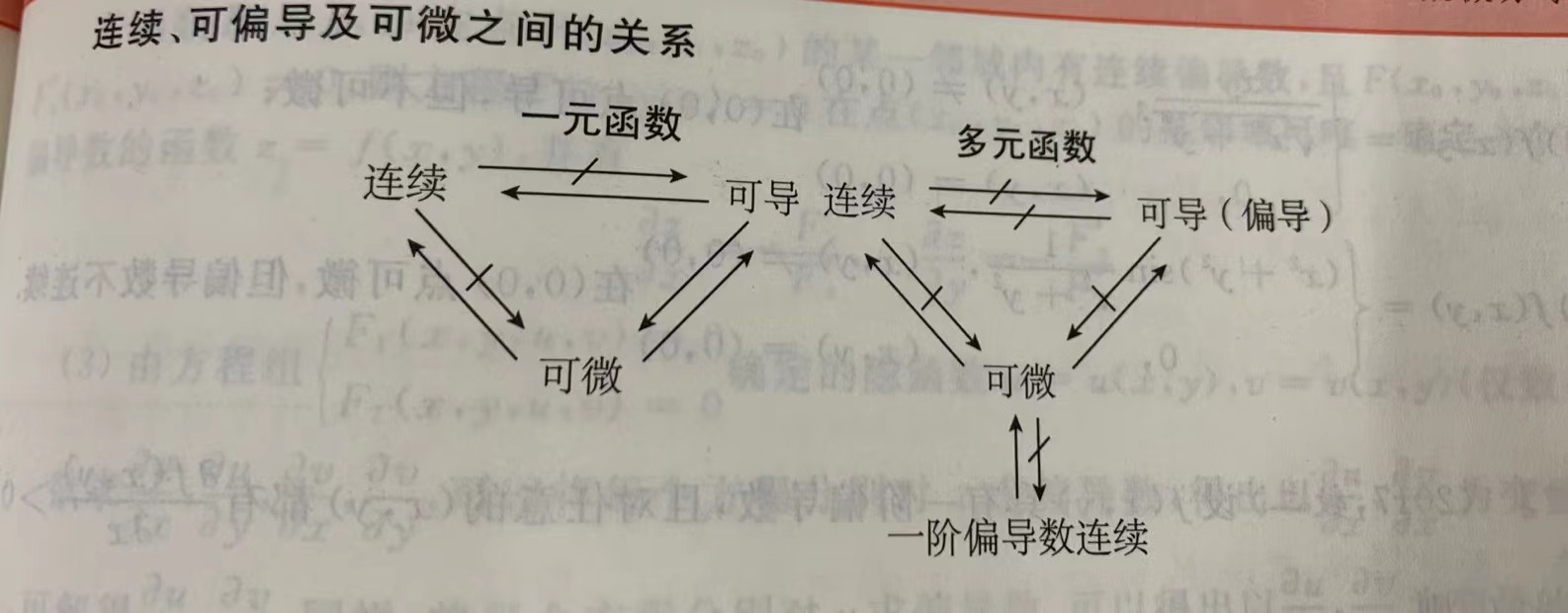
偏导数的定义
二元函数偏导数的几何意义
高阶偏导数
全微分
偏导数的定义
偏导数是一种特殊的数学概念,它是针对一个多变量的函数在某个自变量上的导数。
具体来说,对于一个有多个自变量的函数y=f(x0, x1, xj, ..., xn),在自变量xk固定的情况下,函数y=f(x0, x1, xj, ..., xn)可以看成是关于自变量x0, x1, xj, ..., xn的函数。当自变量xk变化时,函数y=f(x0, x1, xj, ..., xn)在固定自变量x0, x1, xj, ..., xn时的值会变化,这时就会用到偏导数来描述这个变化。
偏导数的计算方法是:将所求偏导数的自变量视为常数,而将其他自变量视为变量,进行求导。例如,对于函数y=f(x0, x1, xj, ..., xn),求y关于x0的偏导数时,将x1, xj, ..., xn视为常数,然后对x0进行求导。
偏导数在许多实际应用中都有重要应用,例如在经济学、工程学和物理学等领域。在经济学中,偏导数可以用来分析某个自变量对经济变量的影响;在工程学中,偏导数可以用来分析某个参数对设计变量的影响;在物理学中,偏导数可以用来描述某个物理量的分布情况。
总之,偏导数是一种针对多变量函数在某个自变量上的导数,它在实际应用中有广泛的应用,并可以用相应的计算公式进行计算。
二元函数偏导数的几何意义
二元函数偏导数的几何意义是表示一个曲面在某一点上的切线斜率。
具体来说,对于一个二元函数z=f(x,y),它代表一个曲面。在某一点(x0,y0)上,偏导数z/x表示该点在x轴上的切线斜率,偏导数z/y表示该点在y轴上的切线斜率。
因此,二元函数偏导数的几何意义可以理解为:在某一点上,沿着对应自变量的方向变化时,函数值的变化率。例如,当沿着x轴方向变化时,z/x给出了函数值的变化率;当沿着y轴方向变化时,z/y给出了函数值的变化率。
高阶偏导数
高阶偏导数是指对多元函数进行多次偏导数的计算。对于二元函数z=f(x, y),其一阶偏导数包括z对x的偏导数z/x和z对y的偏导数z/y。而二阶偏导数则包括z对x的二阶偏导数z/x^2、z对y的二阶偏导数z/y^2和z对x和y的混合偏导数z/(xy)。
对于高阶偏导数,其计算方法与一阶偏导数类似,只是需要对每个自变量分别求偏导数的次数更多。例如,对于二元函数z=f(x, y),其三阶偏导数包括z对x的三阶偏导数z/x^3、z对y的三阶偏导数z/y^3、z对x和y的混合偏导数z/(xy^2)、z对x和y的混合偏导数z/(x^2y)和z对x和y的混合偏导数z/(xy^2)。
高阶偏导数的计算可以使用公式进行,也可以使用数学软件或符号计算系统进行计算。在实际应用中,高阶偏导数可以用于描述函数的高阶性质,例如在物理学和工程学中用于描述物理量的高阶分布。
全微分
高阶导数的全微分是指对多元函数进行多次全微分的计算。
对于二元函数z=f(x, y),其一阶全微分包括dz/dx和dz/dy。而二阶全微分则包括d^2z/dx^2、d^2z/dy^2和d^2z/dxdy。
对于高阶全微分,其计算方法与一阶全微分类似,只是需要对每个自变量分别求全微分的次数更多。例如,对于二元函数z=f(x, y),其三阶全微分包括d^3z/dx^3、d^3z/dy^3、d^3z/dxdy^2、d^3z/dx^2dy和d^3z/dxdy^2。
高阶全微分可以使用公式进行计算,也可以使用数学软件或符号计算系统进行计算。在实际应用中,高阶全微分可以用于描述函数的高阶性质,例如在物理学和工程学中用于描述物理量的高阶分布。