1、概述
在深度学习的训练模型过程中,参数的优化是一个比较繁琐的过程,一般使用网格搜索Grid search与人工搜索Manual search,所以这个参数优化有时候看起来就像太上老君炼丹,是一个有点玄的东西。
那有没有一种可以自动去调优的工具呢?恩,本节介绍的这个Hyperopt工具就是这个用途。
Hyperopt是一个Python库,用于在复杂的搜索空间(可能包括实值、离散和条件维度)上进行串行和并行优化。
Hyperopt目前实现了三种算法:
Random Search
Tree of Parzen Estimators (TPE)
Adaptive TPE
Hyperopt的设计是为了适应基于高斯过程和回归树的贝叶斯优化算法,但这些算法目前还没有实现。所有算法都可以通过下面两种方式并行化:
Apache Spark
MongoDB
一个是大数据处理引擎,另一个是分布式数据库。
2、安装hyperopt
安装(依然建议加上豆瓣镜像)
pip3 install --user hyperopt -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com
可以看到安装了下面这些模块:
Successfully built future
Installing collected packages: zipp, numpy, importlib-resources, decorator, tqdm, scipy, py4j, networkx, future, cloudpickle, hyperopt
Successfully installed cloudpickle-2.2.1 decorator-4.4.2 future-0.18.3 hyperopt-0.2.7 importlib-resources-5.4.0 networkx-2.5.1 numpy-1.19.5 py4j-0.10.9.7 scipy-1.5.4 tqdm-4.64.1 zipp-3.6.0
3、测试
3.1、hyperopt_test.py
安装好了之后,我们来测试一个示例:
gedit hyperopt_test.pyfrom hyperopt import fmin, tpe, space_eval,hp
def objective(args):
case, val = args
if case == 'case 1':
return val
else:
return val ** 2
# define a search space
space = hp.choice('a',
[
('case 1', 1 + hp.lognormal('c1', 0, 1)),
('case 2', hp.uniform('c2', -10, 10))
])
# minimize the objective over the space
best = fmin(objective, space, algo=tpe.suggest, max_evals=100)
print(best)
print(space_eval(space, best))
best2 = fmin(fn=lambda x: x ** 2,
space=hp.uniform('x', -8, -2),
algo=tpe.suggest,
max_evals=200)
print(best2)
运行:
python3 hyperopt_test.py
'''
100%|██████████████████████████████████████████████████████████████████████████| 100/100 [00:00<00:00, 269.38trial/s, best loss: 6.787702954398033e-05]
{'a': 1, 'c2': -0.008238751698162794}
('case 2', -0.008238751698162794)
100%|██████████████████████████████████████████████████████████████████████████████| 200/200 [00:00<00:00, 335.54trial/s, best loss: 4.000953693453848]
{'x': -2.000238409153731}
'''其中objective这个就是目标函数,通过fmin函数使目标函数最小,那么得到的就是最佳参数。
结果返回的是字典类型,迭代过程可以显示进度条(verbose=False禁用不显示),前面best迭代100次,后面best2那个迭代200次,以及最小损失函数和优化后的结果。
3.2、fmin函数
这里关键点是fmin函数,我们查看这个函数的帮助文档help(fmin):
fmin(fn, space, algo=None, max_evals=None, timeout=None, loss_threshold=None, trials=None, rstate=None, allow_trials_fmin=True, pass_expr_memo_ctrl=None, catch_eval_exceptions=False, verbose=True, return_argmin=True, points_to_evaluate=None, max_queue_len=1, show_progressbar=True, early_stop_fn=None, trials_save_file='')
Minimize a function over a hyperparameter space.
#最小化超参数空间上的函数
More realistically: *explore* a function over a hyperparameter space
according to a given algorithm, allowing up to a certain number of
function evaluations. As points are explored, they are accumulated in
`trials`
Parameters
----------
fn : callable (trial point -> loss)
This function will be called with a value generated from `space`
as the first and possibly only argument. It can return either
a scalar-valued loss, or a dictionary. A returned dictionary must
contain a 'status' key with a value from `STATUS_STRINGS`, must
contain a 'loss' key if the status is `STATUS_OK`. Particular
optimization algorithms may look for other keys as well. An
optional sub-dictionary associated with an 'attachments' key will
be removed by fmin its contents will be available via
`trials.trial_attachments`. The rest (usually all) of the returned
dictionary will be stored and available later as some 'result'
sub-dictionary within `trials.trials`.
space : hyperopt.pyll.Apply node or "annotated"
The set of possible arguments to `fn` is the set of objects
that could be created with non-zero probability by drawing randomly
from this stochastic program involving involving hp_<xxx> nodes
(see `hyperopt.hp` and `hyperopt.pyll_utils`).
If set to "annotated", will read space using type hint in fn. Ex:
(`def fn(x: hp.uniform("x", -1, 1)): return x`)
algo : search algorithm
This object, such as `hyperopt.rand.suggest` and
`hyperopt.tpe.suggest` provides logic for sequential search of the
hyperparameter space.
max_evals : int
Allow up to this many function evaluations before returning.
timeout : None or int, default None
Limits search time by parametrized number of seconds.
If None, then the search process has no time constraint.
loss_threshold : None or double, default None
Limits search time when minimal loss reduced to certain amount.
If None, then the search process has no constraint on the loss,
and will stop based on other parameters, e.g. `max_evals`, `timeout`
trials : None or base.Trials (or subclass)
Storage for completed, ongoing, and scheduled evaluation points. If
None, then a temporary `base.Trials` instance will be created. If
a trials object, then that trials object will be affected by
side-effect of this call.
rstate : numpy.random.Generator, default numpy.random or `$HYPEROPT_FMIN_SEED`
Each call to `algo` requires a seed value, which should be different
on each call. This object is used to draw these seeds via `randint`.
The default rstate is
`numpy.random.default_rng(int(env['HYPEROPT_FMIN_SEED']))`
if the `HYPEROPT_FMIN_SEED` environment variable is set to a non-empty
string, otherwise np.random is used in whatever state it is in.
verbose : bool
Print out some information to stdout during search. If False, disable
progress bar irrespectively of show_progressbar argument
allow_trials_fmin : bool, default True
If the `trials` argument
pass_expr_memo_ctrl : bool, default False
If set to True, `fn` will be called in a different more low-level
way: it will receive raw hyperparameters, a partially-populated
`memo`, and a Ctrl object for communication with this Trials
object.
return_argmin : bool, default True
If set to False, this function returns nothing, which can be useful
for example if it is expected that `len(trials)` may be zero after
fmin, and therefore `trials.argmin` would be undefined.
points_to_evaluate : list, default None
Only works if trials=None. If points_to_evaluate equals None then the
trials are evaluated normally. If list of dicts is passed then
given points are evaluated before optimisation starts, so the overall
number of optimisation steps is len(points_to_evaluate) + max_evals.
Elements of this list must be in a form of a dictionary with variable
names as keys and variable values as dict values. Example
points_to_evaluate value is [{'x': 0.0, 'y': 0.0}, {'x': 1.0, 'y': 2.0}]
Returns
-------
argmin : dictionary
If return_argmin is True returns `trials.argmin` which is a dictionary. Otherwise
this function returns the result of `hyperopt.space_eval(space, trails.argmin)` if there
were successfull trails. This object shares the same structure as the space passed.
If there were no successfull trails, it returns None.
max_queue_len : integer, default 1
Sets the queue length generated in the dictionary or trials. Increasing this
value helps to slightly speed up parallel simulatulations which sometimes lag
on suggesting a new trial.
show_progressbar : bool or context manager, default True (or False is verbose is False).
Show a progressbar. See `hyperopt.progress` for customizing progress reporting.
early_stop_fn: callable ((result, *args) -> (Boolean, *args)).
Called after every run with the result of the run and the values returned by the function previously.
Stop the search if the function return true.
Default None.
trials_save_file: str, default ""
Optional file name to save the trials object to every iteration.
If specified and the file already exists, will load from this file when
trials=None instead of creating a new base.Trials object3.3、可视化函数
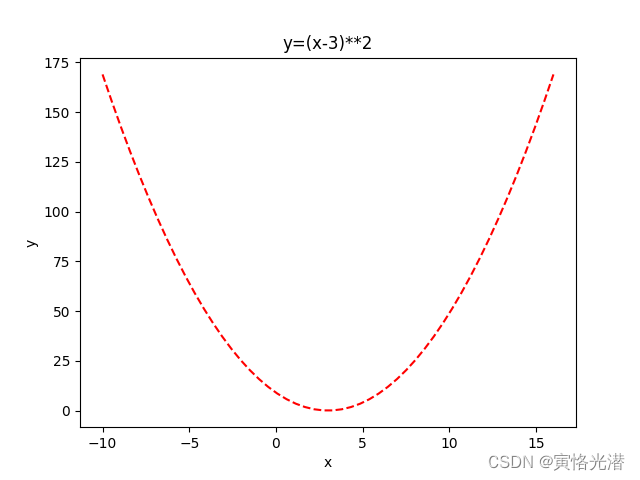
我们再来看一个y=(x-3)²的示例,先画出这个函数的图,这样看起来更直观一点:
import numpy as np
import matplotlib.pylab as plt
x=np.linspace(-10,16)
y=(x-3)**2
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x,y,'r--',label='(x-3)**2')
plt.title("y=(x-3)**2")
#plt.legend()
plt.show()如下图:
更多画图技巧,可以查阅:Python画图(直方图、多张子图、二维图形、三维图形以及图中图)
从图中我们可以看到,让函数最小化的值,x为3,当然这个不看图也可以知道,好了,现在我们来测试下:
best = fmin(
fn=lambda x: (x-3)**2,
space=hp.uniform('x', -10, 10),
algo=tpe.suggest,
max_evals=100)
print(best)
#{'x': 2.967563715953902}试着将max_evals最大迭代次数调到1000,看下结果是怎么样的,将更接近于3了。
3.4、hp范围值
space为空间搜索范围,其中这里面的hp包含有下面的取值方法:
'choice', 'lognormal', 'loguniform', 'normal', 'pchoice', 'qlognormal', 'qloguniform', 'qnormal', 'quniform', 'randint', 'uniform', 'uniformint'需要注意的是,normal正态分布的返回值,限制不了范围,我们来做一个对比测试:
from hyperopt import hp
import hyperopt.pyll.stochastic
space = {
'x':hp.uniform('x', 0, 1),
'y':hp.normal('y', 0, 1),
'z':hp.randint('z',0,10),
'c':hp.choice('City', ['GuangZhou','ShangHai', 'BeiJing']),
}>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'GuangZhou', 'x': 0.38603237555669656, 'y': -0.19782139601114704, 'z': array(1)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'ShangHai', 'x': 0.7838648171908386, 'y': 0.43014722187588245, 'z': array(8)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'BeiJing', 'x': 0.5137264208587933, 'y': -0.10021079359026988, 'z': array(4)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'BeiJing', 'x': 0.7201793839228087, 'y': 0.11571302115909506, 'z': array(0)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'GuangZhou', 'x': 0.21906317438496536, 'y': -1.645732195658909, 'z': array(0)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'ShangHai', 'x': 0.17319873908122796, 'y': -0.7472225692827178, 'z': array(4)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'GuangZhou', 'x': 0.4376348587045986, 'y': 0.7303201600143362, 'z': array(7)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'BeiJing', 'x': 0.43311251571433906, 'y': 1.216596288611056, 'z': array(1)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'BeiJing', 'x': 0.17755989388617366, 'y': 0.3168677593459059, 'z': array(4)}
>>> print(hyperopt.pyll.stochastic.sample(space))
{'c': 'GuangZhou', 'x': 0.6058631246917083, 'y': -0.2849664724345445, 'z': array(1)}可以看到输出的样本空间中,其中正态分布y的值,出现了负数,其他的都是在限定范围内。
3.5、Trials追踪
Trials用来了解在迭代过程中的一些返回信息,我们来看个示例:
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
fspace = {
'x': hp.uniform('x', -5, 5)
}
def f(params):
x = params['x']
val = (x-3)**2
return {'loss': val, 'status': STATUS_OK}
trials = Trials()
best = fmin(fn=f, space=fspace, algo=tpe.suggest, max_evals=50, trials=trials)
print(best)
#{'x': 2.842657137743265}
for trial in trials.trials[:5]:
print(trial)
'''
{'state': 2, 'tid': 0, 'spec': None, 'result': {'loss': 12.850632865897229, 'status': 'ok'}, 'misc': {'tid': 0, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'workdir': None, 'idxs': {'x': [0]}, 'vals': {'x': [-0.5847779381570106]}}, 'exp_key': None, 'owner': None, 'version': 0, 'book_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 615000), 'refresh_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 615000)}
{'state': 2, 'tid': 1, 'spec': None, 'result': {'loss': 23.862240347848957, 'status': 'ok'}, 'misc': {'tid': 1, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'workdir': None, 'idxs': {'x': [1]}, 'vals': {'x': [-1.884899215730961]}}, 'exp_key': None, 'owner': None, 'version': 0, 'book_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 616000), 'refresh_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 616000)}
{'state': 2, 'tid': 2, 'spec': None, 'result': {'loss': 42.84157056715999, 'status': 'ok'}, 'misc': {'tid': 2, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'workdir': None, 'idxs': {'x': [2]}, 'vals': {'x': [-3.545347245728067]}}, 'exp_key': None, 'owner': None, 'version': 0, 'book_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 616000), 'refresh_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 617000)}
{'state': 2, 'tid': 3, 'spec': None, 'result': {'loss': 0.8412634189024095, 'status': 'ok'}, 'misc': {'tid': 3, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'workdir': None, 'idxs': {'x': [3]}, 'vals': {'x': [3.9172041315336568]}}, 'exp_key': None, 'owner': None, 'version': 0, 'book_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 617000), 'refresh_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 617000)}
{'state': 2, 'tid': 4, 'spec': None, 'result': {'loss': 30.580983627886543, 'status': 'ok'}, 'misc': {'tid': 4, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'workdir': None, 'idxs': {'x': [4]}, 'vals': {'x': [-2.5300075612865616]}}, 'exp_key': None, 'owner': None, 'version': 0, 'book_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 618000), 'refresh_time': datetime.datetime(2023, 9, 12, 5, 24, 57, 618000)}
'''同样的我们可以根据上面这些迭代的信息,将它们画出来,这样看起来就比较直观了:
import matplotlib.pylab as plt
x=[t['misc']['vals']['x'] for t in trials.trials]
y=[t['result']['loss'] for t in trials.trials]
plt.xlabel('x')
plt.ylabel('y')
plt.scatter(x,y,c='r')
plt.show()如图:
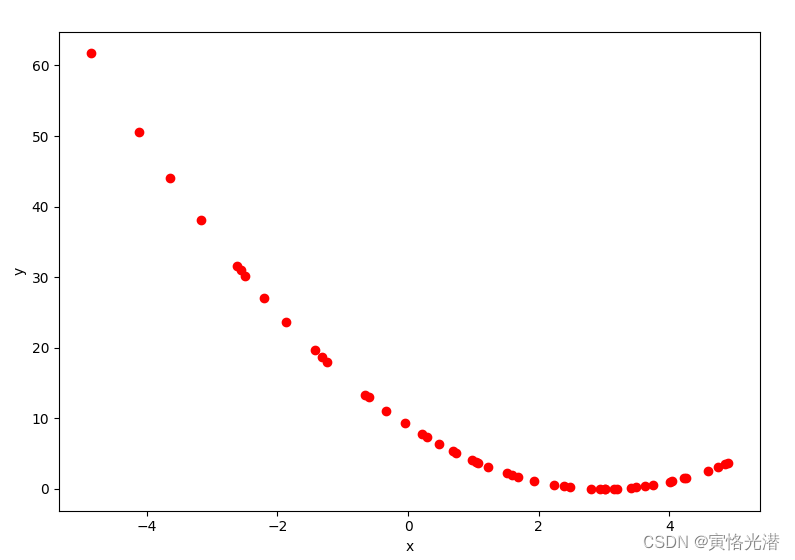
可以看到在3附近的地方得到的是函数的最小值。
关于更多散点图的知识,可以查阅:Python画图之散点图(plt.scatter)
题外话:这里的Trials我感觉这个库应该是误写了,正确的单词应该是Trails,有踪迹的意思,而Trials的意思是努力和尝试等含义。
4、实际应用
有了上面知识的铺垫,我们接下来测试下实际当中的应用效果,先来看一个K最近邻的示例,使用的是鸢尾花iris的数据集(150个样本的三个类setosa,versicolor,virginica):
4.1、K最近邻KNN
先安装相应的库,已安装的忽略
pip3 install --user scikit-learn -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com接下来就上代码:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
from hyperopt import hp,STATUS_OK,Trials,fmin,tpe
iris=load_iris()
X=iris.data
y=iris.target
def hyperopt_train(params):
clf=KNeighborsClassifier(**params)
return cross_val_score(clf,X,y).mean()
space_knn={'n_neighbors':hp.choice('n_neighbors',range(1,50))}
def f(parmas):
acc=hyperopt_train(parmas)
return {'loss':-acc,'status':STATUS_OK}
trials=Trials()
best=fmin(f,space_knn,algo=tpe.suggest,max_evals=100,trials=trials)
print(best)
#{'n_neighbors': 6}同样我们将其画图来直观感受下:
import matplotlib.pylab as plt
x=[t['misc']['vals']['n_neighbors'] for t in trials.trials]
y=[-t['result']['loss'] for t in trials.trials]
plt.xlabel('n_neighbors')
plt.ylabel('cross_val_score')
plt.scatter(x,y,c='r')
plt.show()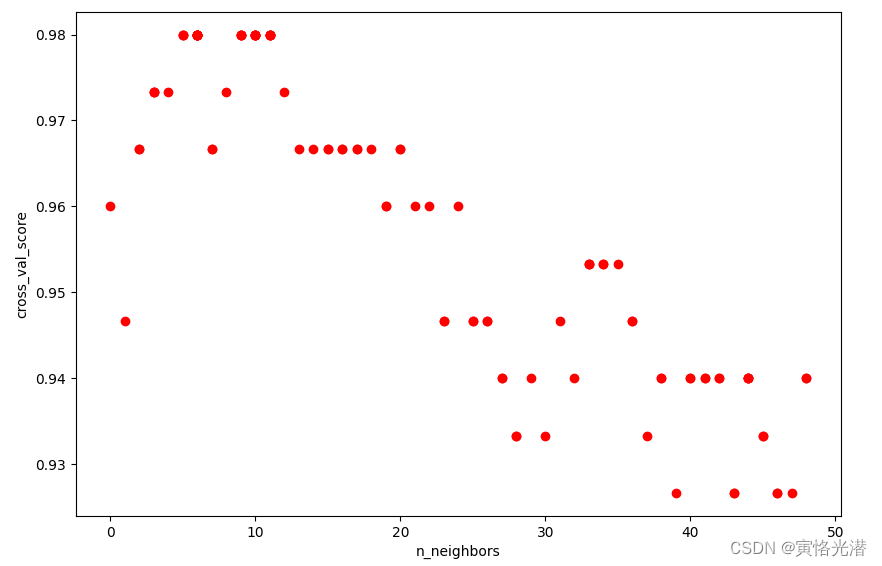
4.2、支持向量分类SVC
再来看下这个鸢尾花数据集在支持向量机中的向量分类会是什么情况:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from hyperopt import hp,STATUS_OK,Trials,fmin,tpe
from sklearn.svm import SVC
iris=load_iris()
X=iris.data
y=iris.target
def hyperopt_train_test(params):
clf =SVC(**params)
return cross_val_score(clf, X, y).mean()
space_svm = {
'C': hp.uniform('C', 0, 20),
'kernel': hp.choice('kernel', ['linear', 'sigmoid', 'poly', 'rbf']),
'gamma': hp.uniform('gamma', 0, 20),
}
def f(params):
acc = hyperopt_train_test(params)
return {'loss': -acc, 'status': STATUS_OK}
trials = Trials()
best = fmin(f, space_svm, algo=tpe.suggest, max_evals=100, trials=trials)
print(best)
#{'C': 0.8930681939735963, 'gamma': 8.379245134714441, 'kernel': 0}同样的画图看下效果:
from matplotlib import pyplot as plt
parameters = ['C', 'kernel', 'gamma']
cols = len(parameters)
f, axes = plt.subplots(1,cols)
for i, val in enumerate(parameters):
xs = [t['misc']['vals'][val] for t in trials.trials]
ys = [-t['result']['loss'] for t in trials.trials]
axes[i].scatter(xs, ys, c="g")
axes[i].set_title(val)
axes[i].set_ylim([0.9, 1.0])
plt.show()如图:

4.3、决策树DecisionTree
再来看下决策树的优化情况,代码都差不多,这里将SVC换成DecisionTreeClassifier,决策树就是看下层数等优化情况:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from hyperopt import hp,STATUS_OK,Trials,fmin,tpe
from sklearn.tree import DecisionTreeClassifier
iris=load_iris()
X=iris.data
y=iris.target
def hyperopt_train_test(params):
clf =DecisionTreeClassifier(**params)
return cross_val_score(clf, X, y).mean()
space_dt = {
'max_depth': hp.choice('max_depth', range(1,20)),
'max_features': hp.choice('max_features', range(1,5)),
'criterion': hp.choice('criterion', ["gini", "entropy"]),
}
def f(params):
acc = hyperopt_train_test(params)
return {'loss': -acc, 'status': STATUS_OK}
trials = Trials()
best = fmin(f, space_dt, algo=tpe.suggest, max_evals=100, trials=trials)
print(best)
#{'criterion': 0, 'max_depth': 17, 'max_features': 1}
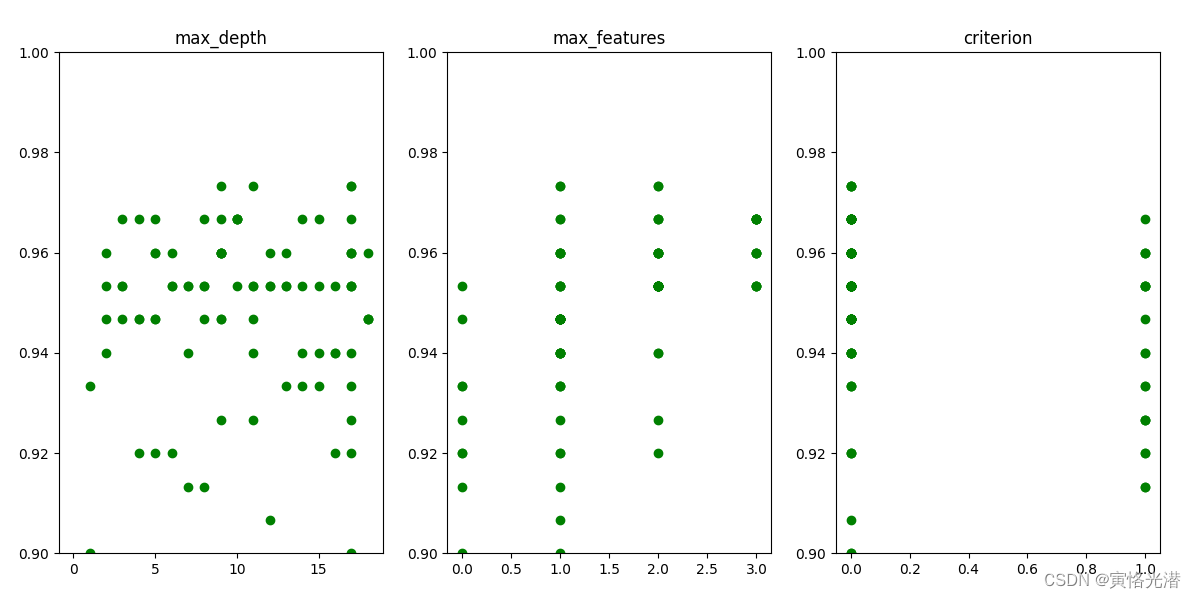
同样的画图看下效果:
from matplotlib import pyplot as plt
parameters = ['max_depth', 'max_features', 'criterion']
cols = len(parameters)
f, axes = plt.subplots(1,cols)
for i, val in enumerate(parameters):
xs = [t['misc']['vals'][val] for t in trials.trials]
ys = [-t['result']['loss'] for t in trials.trials]
axes[i].scatter(xs, ys, c="g")
axes[i].set_title(val)
axes[i].set_ylim([0.9, 1.0])
plt.show()如图:
5、小结
通过对hyperopt的认识,这样我们就可以在后期的工作中来高效寻找最优参数了,主要就是通过fmin()这个方法里面设定需要优化的损失函数,以及寻找的空间范围值,然后进行迭代找出最佳值。我们还可以指定Trials()来追踪迭代的信息,并对其进行了画图可视化,便于我们更直观的观察。
关于寻找最优参数与超参数的一些技巧的文章:
神经网络技巧篇之寻找最优参数的方法
神经网络技巧篇之寻找最优参数的方法【续】
神经网络技巧篇之寻找最优超参数
github:https://github.com/hyperopt/hyperopt