题目：

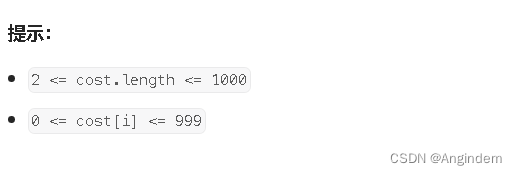
思路：

        根据题意，我们先明确 dp 数组 i 的含义，  这里很明显，可以知道 i 是对应阶梯的最少花费，

其次dp初始化中，我们的 dp[0] 和 dp[1]  是 0 花费，

这是我们可以选择的，到了 dp[2] 就是我们min(dp[0] + cost[0],dp[1] + cost[1])   

即   这就是 我们的递推公式：达到当前阶梯的最少花费 + 当前阶梯需要的花费 = 到达的目标阶梯

即 dp[i] = min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2])；

代码详解如下：

int minCostClimbingStairs(vector<int>& cost) 
{
	// 计算台阶数量
	int n =cost.size();
    
    // 定义 dp 数组，其中 dp[i]  
	// i 所对应的是相应台阶的最少花费
    vector<int>dp(n + 1,0);
    
    // dp 数组初始化，由于可以选择在 0 或 1 台阶开始爬楼梯
    // 所以 先计算第三个台阶的最少花费
    dp[2] = min(cost[0],cost[1]);
    
    for(int i = 3;i <= n;++i)
    {
    	// 递推公式，达到当前阶梯的最少花费 + 当前阶梯需要的花费 = 到达的目标阶梯
    	dp[i] = min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);
	}
	
	/*
	
	打印 dp 数组查看是否是自己需要的效果
	验证答案
	debugv(dp);
	
	*/
    
    // 输出对应阶梯的最少花费
	return dp[n];
}

最后提交：