原文：

https://zhuanlan.zhihu.com/p/567560364

1）0-1背包问题的描述

现在有四种物品，每种物品只有1件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

物品编号	物品重量	物品价值	物品数量
1	2	3	1
2	3	4	1
3	4	5	1
4	5	8	1

（2）多重背包问题的描述

现在有四种物品，每种物品有若干件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

物品编号	物品重量	物品价值	物品数量
1	2	3	2
2	3	4	2
3	4	5	2
4	5	8	2

（3）完全背包问题的描述

现在有四种物品，每种物品有无数件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

物品编号	物品重量	物品价值	物品数量
1	2	3	无数件
2	3	4	无数件
3	4	5	无数件
4	5	8	无数件

一、0-1背包问题

一、0-1背包问题

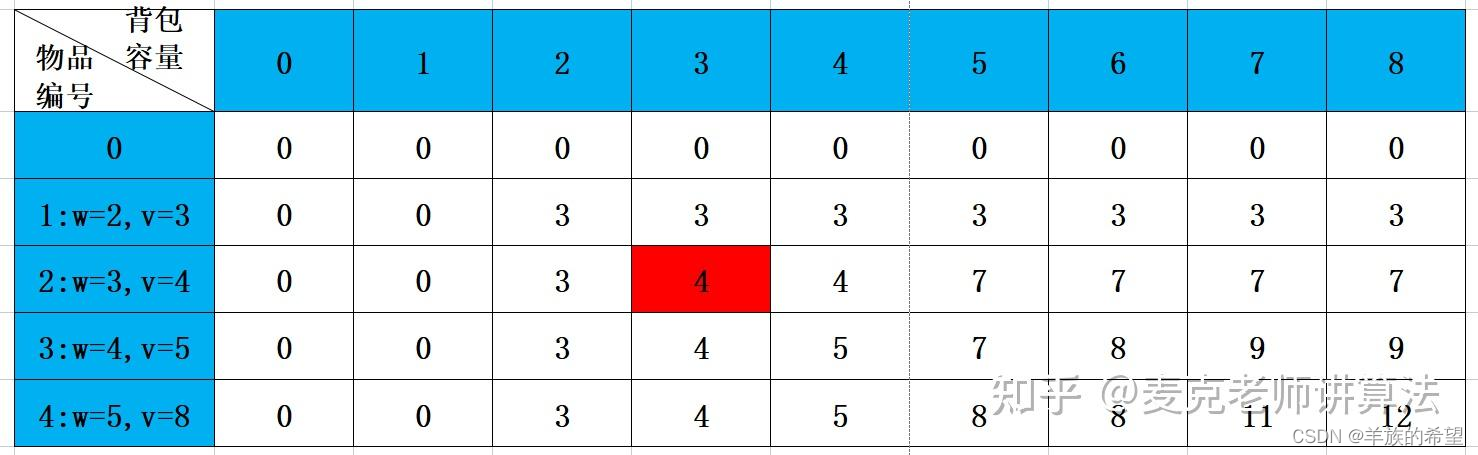
思路：对于每件物品，由于是不可分割的放入，所以，就有两种情况：该物品放入背包与该物品不放入背包；为了将以上问题求解出来，我们需要设置好状态以及状态转移方程。

（1）定义状态

DP[k][w]:表示当背包剩余容量为w，现在有前k件物品可放的情况下，背包所能装物品的最大价值。

那么，状态确定好了，上面所描述的题目中，只要求出DP[4][8]就可以了。

DP[k][w]怎么求呢，这就是状态转移方程的问题。

（2）状态转移方程

我们先将状态转移方程写出来吧，就是：

DP[k][w] 等于下列两种情况：

①DP[k][w]=DP[k-1][w]，当第k件物品的重量大于w时

②DP[k][w]=max(DP[k-1][w]，DP[k-1][w-wi])，当第k件物品的重量不大于w时

#include <stdio.h>

#define N 10010
#define V 10010
#define MAX(a,b) ((a) > (b) ? (a) : (b))

int dp[N][V];
int n, v;       //n:物品数量，v:背包实际容量 
int weight[N];   //第n件物品的重量 
int value[N];    //第n件物品的价值 

void knap_01()
{
    for (int i = 1;i <= n; i++)
        for (int j = 1; j <= v; j++) {
            if (weight[i] > j) {
                dp[i][j] = dp[i-1][j];
            } else {
                dp[i][j] = MAX(dp[i - 1][j - weight[i]] + value[i], dp[i - 1][j]);
            }
    }
}

int main()
{
    scanf("%d %d", &n, &v);
    for(int i = 1;i <= n; i++) {
        scanf("%d", &weight[i]);
    }

    for(int i = 1;i <= n; i++) {
        scanf("%d", &value[i]);
    }

    knap_01();
    printf("dp[%d][%d]=%d\n", n, v, dp[n][v]);

    return 0;
}