2023年五一杯数学建模
B题 快递需求分析问题
原题再现:
网络购物作为一种重要的消费方式,带动着快递服务需求飞速增长,为我国经济发展做出了重要贡献。准确地预测快递运输需求数量对于快递公司布局仓库站点、节约存储成本、规划运输线路等具有重要的意义。附件1、附件2、附件3为国内某快递公司记录的部分城市之间的快递运输数据,包括发货日期、发货城市以及收货城市(城市名已用字母代替,剔除了6月、11月、12月的数据)。请依据附件数据,建立数学模型,完成以下问题:
问题1:附件1为该快递公司记录的2018年4月19日—2019年4月17日的站点城市之间(发货城市-收货城市)的快递运输数据,请从收货量、发货量、快递数量增长/减少趋势、相关性等多角度考虑,建立数学模型,对各站点城市的重要程度进行综合排序,并给出重要程度排名前5的站点城市名称,将结果填入表1。

问题2:请利用附件1数据,建立数学模型,预测2019年4月18日和2019年4月19日各“发货-收货”站点城市之间快递运输数量,以及当日所有“发货-收货”站点城市之间的总快递运输数量,并在表2中填入指定的站点城市之间的快递运输数量,以及当日所有“发货-收货”站点城市之间的总快递运输数量。

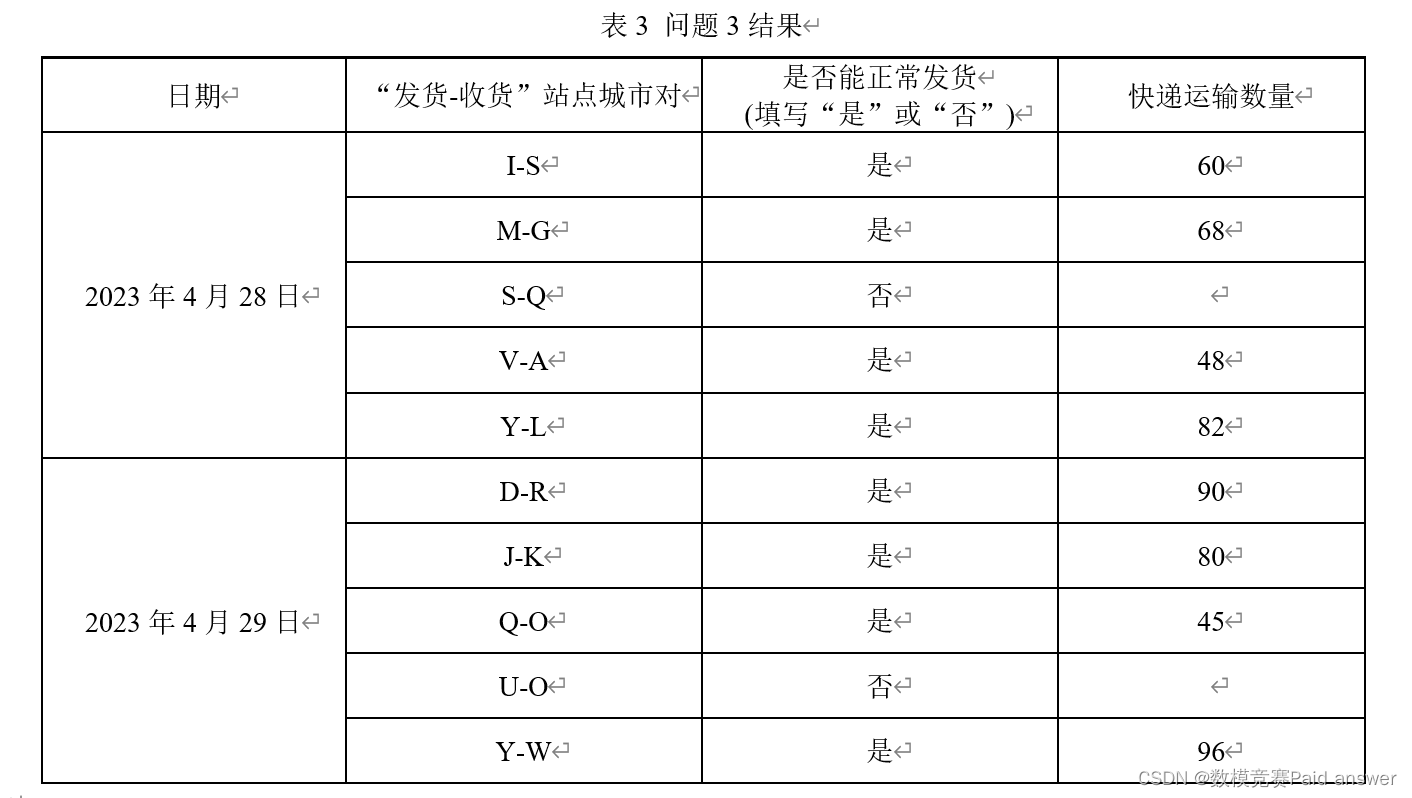
问题3:附件2为该快递公司记录的2020年4月28日—2023年4月27日的快递运输数量。由于受到突发事件影响,部分城市之间快递线路无法正常运输,导致站点城市之间无法正常发货或收货(无数据表示无法正常收发货,0表示无发货需求)。请利用附件2数据,建立数学模型,预测2023年4月28日和2023年4月29日可正常“发货-收货”的站点城市对(发货城市-收货城市),并判断表3中指定的站点城市对是否能正常发货,如果能正常发货,给出对应的快递运输数量,并将结果填入表3。
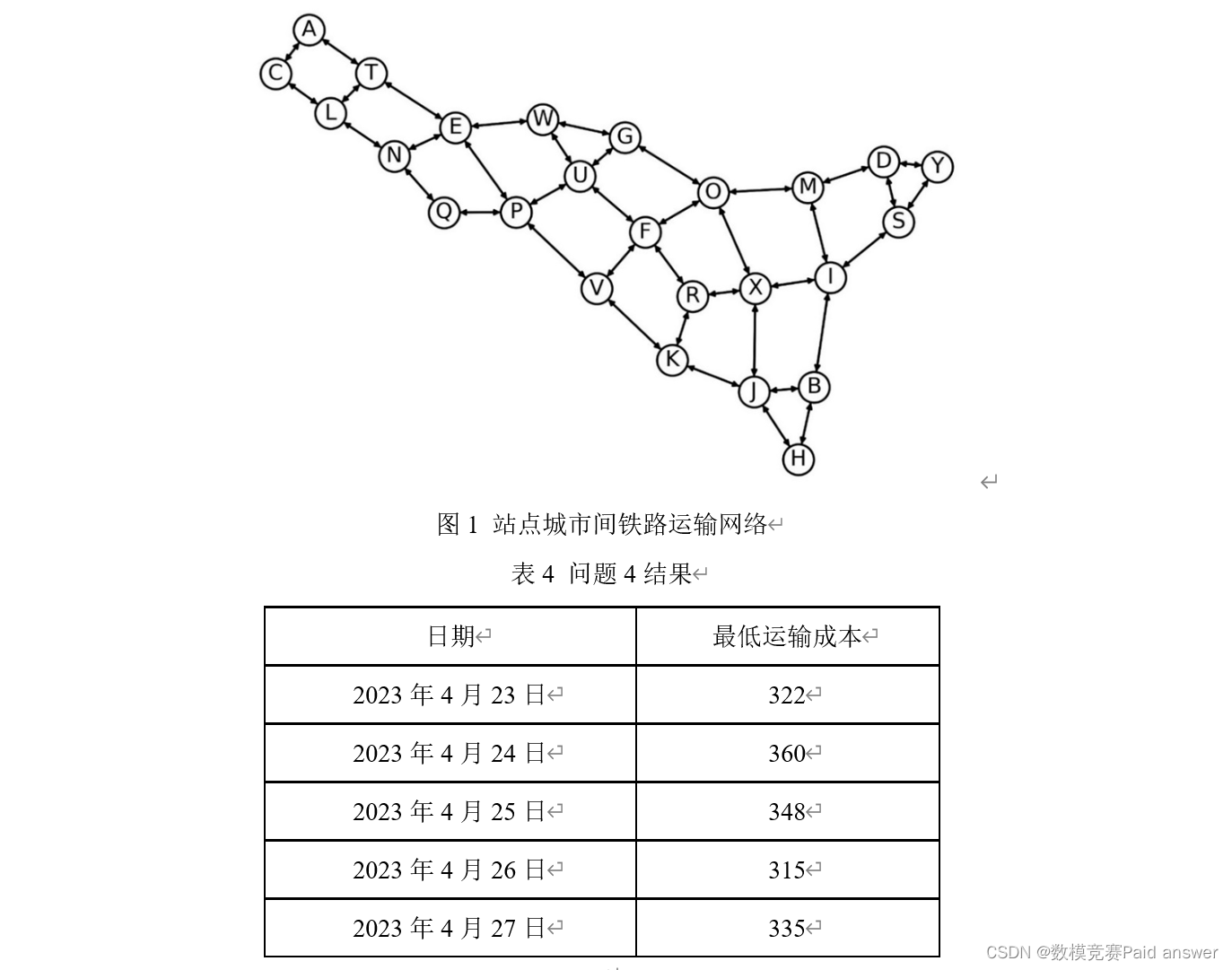
问题4:图1给出了所有站点城市间的铁路运输网络,铁路运输成本由以下公式计算:成本=固定成本×[1+(实际装货量/额定装货量)^3 ]。在本题中,假设实际装货量允许超过额定装货量。所有铁路的固定成本、额定装货量在附件3中给出。在运输快递时,要求每个“发货-收货”站点城市对之间使用的路径数不超过5条,请建立数学模型,给出该快递公司成本最低的运输方案。利用附件2和附件3的数据,计算该公司2023年4月23—27日每日的最低运输成本,填入表4。
备注:为了方便计算,不对快递重量和大小进行区分,假设每件快递的重量为单位1。仅考虑运输成本,不考虑中转等其它成本。
问题5:通常情况下,快递需求由两部分组成,一部分为固定需求,这部分需求来源于日常必要的网购消费(一般不能简单的认定为快递需求历史数据的最小值,通常小于需求的最小值);另一部分为非固定需求,这部分需求通常有较大波动,受时间等因素的影响较大。假设在同一季度中,同一“发货-收货”站点城市对的固定需求为一确定常数(以下简称为固定需求常数);同一“发货-收货”站点城市对的非固定需求服从某概率分布(该分布的均值和标准差分别称为非固定需求均值、非固定需求标准差)。请利用附件2中的数据,不考虑已剔除数据、无发货需求数据、无法正常发货数据,解决以下问题。
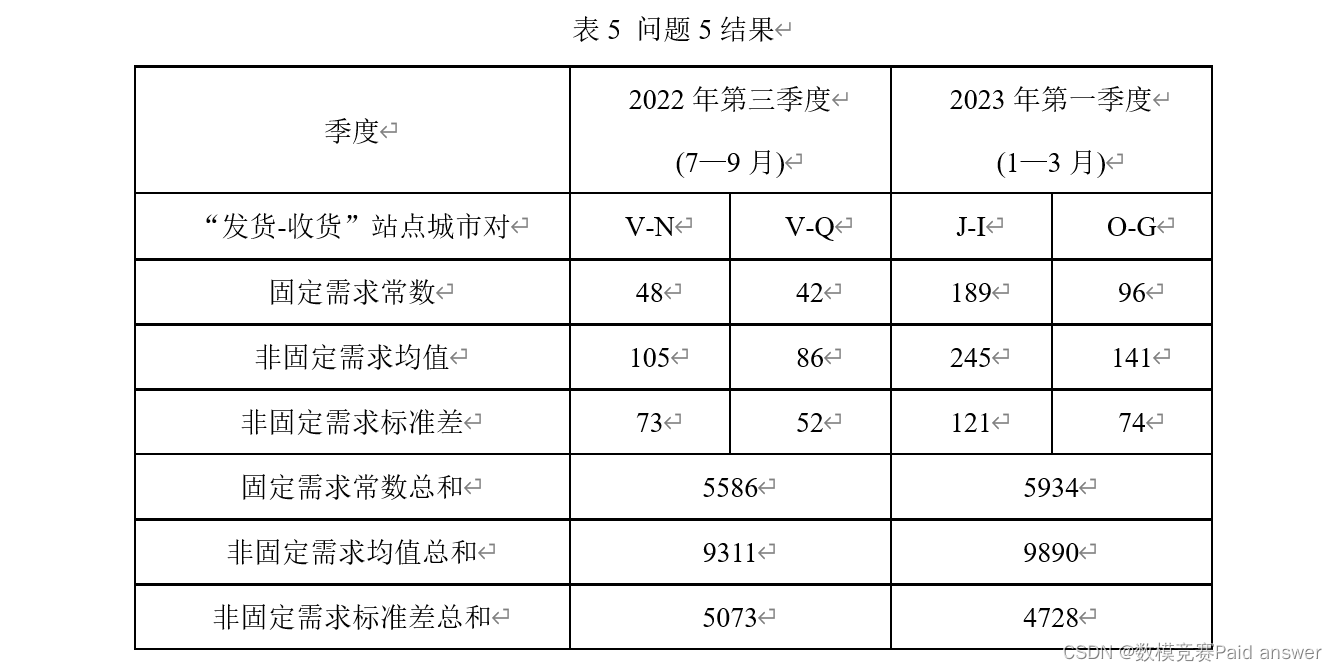
(1) 建立数学模型,按季度估计固定需求常数,并验证其准确性。将指定季度、指定“发货-收货”站点城市对的固定需求常数,以及当季度所有“发货-收货”城市对的固定需求常数总和,填入表5。
(2) 给出非固定需求概率分布估计方法,并将指定季度、指定“发货-收货”站点城市对的非固定需求均值、标准差,以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和,填入表5。
整体求解过程概述(摘要)
网络购物正带动着快递服务需求快速增长,为我国经济发展做出了重要贡献。为节约成本,规划运输线路等问题,急需准确预测快递运输需求数量。
针对问题 1,对附件 1 数据进行描述性统计分析,计算不同站点城市的发货和收货快递数量总和,对站点城市进行重要性初步排序。然后随机选择几个站点城市,绘制非线性拟合曲线图,探究快递数量和日期的联系。结合收发货量和时间日期的影响,对站点城市进行重要程度排名。
针对问题 2,首先对数据进行可视化处理,对附件 1 的数据,绘制 M-U,Q-V,K-L,G-V,V-G,A-Q,D-A,L-K 八条线路快递运输数量的质量分布直方图,对数据进行可视化处理以得到不同路线的缺失值情况。根据缺失值占比不同情况,分布将不同线路数据带入非平稳时间序列模型,预测题中要求站点城市指定日期快递运输数量。
针对问题 3,首先对附件 2 中指定站点城市快递运输缺失日期进行数据挖掘,比对分析不同站点城市的快递运输缺失日期,得出影响站点城市快递运输数量变化的主要因素为节假日,并考虑实际因素,如疫情和政策等因素。接着,使用灰色关联分析方法,结合多种影响因素,得出不同影响因素的权重,并基于此预测指定站点城市的发货情况和快递运输数量。
针对问题 4,建立基于最短路径算法的成本优化模型,根据所给的铁路运输线路图和数据信息,找到源点到其余所有点的最短路径。通过聚类,将四个点分成两部分,分别以发货点和收获点为中心向对应路径进行遍历。综合处理后,每个节点之间的连线和节点均满足约束条件,将连线长度作为权重构建赋权图,使用 Dijkstra算法求得 2023 年 4 月 23-27 日每日的最低运输成本。
针对问题 5,根据问题五中(1)的要求,采用季节系数法估计以 2022 年第三季度V 为发货城市,N 和 Q 为收货城市;以 2023 年第一季度 J 和 O 为发货城市,I 和 G为收货城市的季度需求常数,预测所有城市 2022 年第三季度和 2023 年第一季度的城市固定需求常数总和。对于问题五中(2)的要求,结合问题三结论,不同季度对于快递运输数量的影响权重也不一致。它们可以促进快递运输数量的增大或减少,其不同季节时间段的快递运输数量服从连续型数据的高斯分布。使用 Python 软件编程,对指定季度指定站点城市对的非固定需求均值、标准差进行计算,并计算当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和。
模型假设:
1. 假设快递运输数量随时间变化而变化,即同一站点城市对的快递运输数量会因为时间的推移而有所变化。
2. 假设不同站点城市对的快递运输数量存在一定的相关性,即某些站点城市之的快递运输数量之间存在一定的相关性。
3. 假设快递运输数量的增长/减少趋势具有一定的周期性,即某些站点城市之间的
快递运输数量会有周期性的变化。
4. 假设不同站点城市对的快递运输数量之间可能存在非线性的相关性,即某些站点城市之间的快递运输数量之间可能存在非线性的关系。
5. 假设站点城市的重要程度与其他城市之间的快递运输量有关,即快递运输量越大的站点城市越重要。
6. 假设站点城市之间的快递运输数量与两个城市之间的距离成反比例关系,即两个城市之间的距离越远,快递运输数量越小。
7. 假设在同一天内,快递运输量与发货城市、收货城市以及运输路线有关。
问题分析:
本题涉及多个数学模型及算法,主要探究影响给定站点城市快递运输数量主要因素,并以此为依据,结合不同题目要求进行预测。
问题一分析:
通过对附件1中的数据进行描述性统计分析,对站点城市重要度进行初步排序。在此基础上建立数学模型,对不同路线快递运输数量进行非线性拟合,对影响站点城市快递运输数量的因素进行拟合探究,得到重要城市排名。
问题二分析:
通过对附件 1 的数据进行数据处理,检查数据完整性。对不完整度达到 30%及以上的数据建立非平稳时间序列模型进行以预测指定日期站点城市快递运输数量。
问题三分析:
通过对历史数据的日期,发货成事,收货城市,快递运输数量关联分析,数据挖掘出指定城市之间快递线路不同时间段内的快递运输数量变化规律,并以此建立数学模型来预测 2023 年 4 月 28 日,29 日指定城市的快递运输数量。
问题四分析:
根据题中所给所有站点城市间的铁路运输线路图,结合附件 2 和附件 3 所给所有站点城市的发货城市、收货城市、快递运输数量、额定装货量、固定成本数据信息,建立基于最短路径算法的成本优化模型,为了使快递公司的运输路线要尽可能的使得成本达到最低,而快递经由中间城市数量越多则距离路径越繁琐,成本越大,需鉴于不同城市不同日期对于快递运输数量的影响权重,对最短路径的成本优化模型进行求解。
问题五分析:
根据问题五中(1)的要求,以 2022 年第三季度 V 为发货城市、以 N 和 Q 为收货城市;以 2023 年第一季度 J 和 O 为发货城市、以 I 和 G 为收货城市作为基础数据采用季节系数法估计其季度需求常数,并将应用合理准确的季节系数分别预测所有城市 2022 年第三季度和 2023 年第一季度的城市固定需求常数总和。针对问题五中(2)的要求,结合上述问题三中得出的快递运输数量与日期时间的变化趋势可视图及问题三中得出的结论,不同季度对于快递运输数量的影响权重也不一致,或是起到促进快递运输数量的增大或是使得快递运输数量减少,其不同季节时间段的快递运输数量服从连续型数据的高斯分布,使用 python 软件编程对指定季度指定“发货-收货”站点城市对的非固定需求均值、标准差,以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和进行计算求解。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
import pandas as pd
df = pd.read_excel("附件 1.xlsx")
df.groupby("发货城市")["快递运输数量
"].sum().reset_index().sort_values(by="快递运输数量")
df.groupby("发货城市")["快递运输数量
"].sum().reset_index().sort_values(by="快递运输数量").to_excel("发货
量.xlsx")
df.groupby("收货城市")["快递运输数量
"].sum().reset_index().sort_values(by="快递运输数量").to_excel("收货
量.xlsx")
from pyecharts import Line
asds = pd.read_excel("分组结果.xlsx",sheet_name='G-L')
line = Line("G-L 城市快递运输数量拟合曲线图")
line.add("",asds['日期'],asds['快递运输数量
'],mark_line=["average"],is_smooth=True ,is_label_show=True,is_random=Tr
ue)
line.render('G-L 城市快递运输数量拟合曲线图.html')
from pyecharts import Line
import pandas as pd
year_population_age=pd.read_excel("分组结果.xlsx",sheet_name='A-O')
line3 = Line("A-O 城市快递运输数量堆叠面积图")
line3.add("",
year_population_age['日期'],
year_population_age['快递运输数量'],
is_fill=True,
area_opacity=0.3,
is_smooth=True,#是否显示平滑曲线, 默认为 False
mark_point=['max'],
is_random=True,
is_stack=True)
line3.render('A-O 城市快递运输数量堆叠面积图.html')
#计算需求常数、均值、标准差
import pandas as pd
df = pd.read_excel("附件 2.xlsx",sheet_name='2022-3')
df.groupby(["发货城市","收货城市"])["快递运输数量
"].mean().reset_index().sort_values(by="快递运输数量")
df1 = df.groupby(["发货城市","收货城市"])["快递运输数量
"].mean().reset_index().sort_values(by="快递运输数量")
df1.to_excel("2022 第三季度.xlsx")
pf = pd.read_excel("附件 2.xlsx",sheet_name='2023-1')
pf.groupby(["发货城市","收货城市"])["快递运输数量
"].mean().reset_index().sort_values(by="快递运输数量")
pf1.to_excel("2023 第一季度.xlsx")
import numpy as np
tf1 = pd.read_excel("附件 2.xlsx",sheet_name='V-N')
tf2 = pd.read_excel("附件 2.xlsx",sheet_name='V-Q')
tf3 = pd.read_excel("附件 2.xlsx",sheet_name='J-I')
tf4 = pd.read_excel("附件 2.xlsx",sheet_name='O-G')
np.std(tf1['快递运输数量'])
np.std(tf2['快递运输数量'])
np.std(tf3['快递运输数量'])
np.std(tf4['快递运输数量'])
df.groupby(["发货城市","收货城市"])["快递运输数量
"].std().reset_index().sort_values(by="快递运输数量").to_excel("2022 第
三季度标准差和.xlsx")
pf.groupby(["发货城市","收货城市"])["快递运输数量
"].std().reset_index().sort_values(by="快递运输数量").to_excel("2023 第
一季度标准差和.xlsx")