Leetcode刷题_链表相关_c++版

news2024/11/29 18:24:20

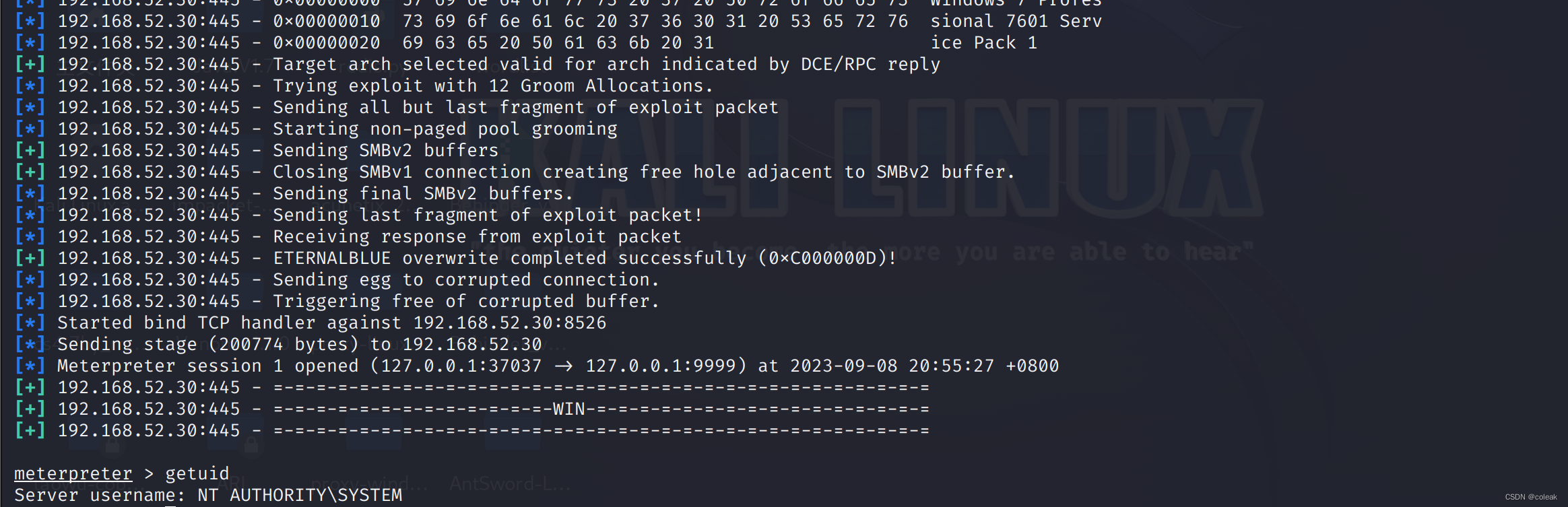
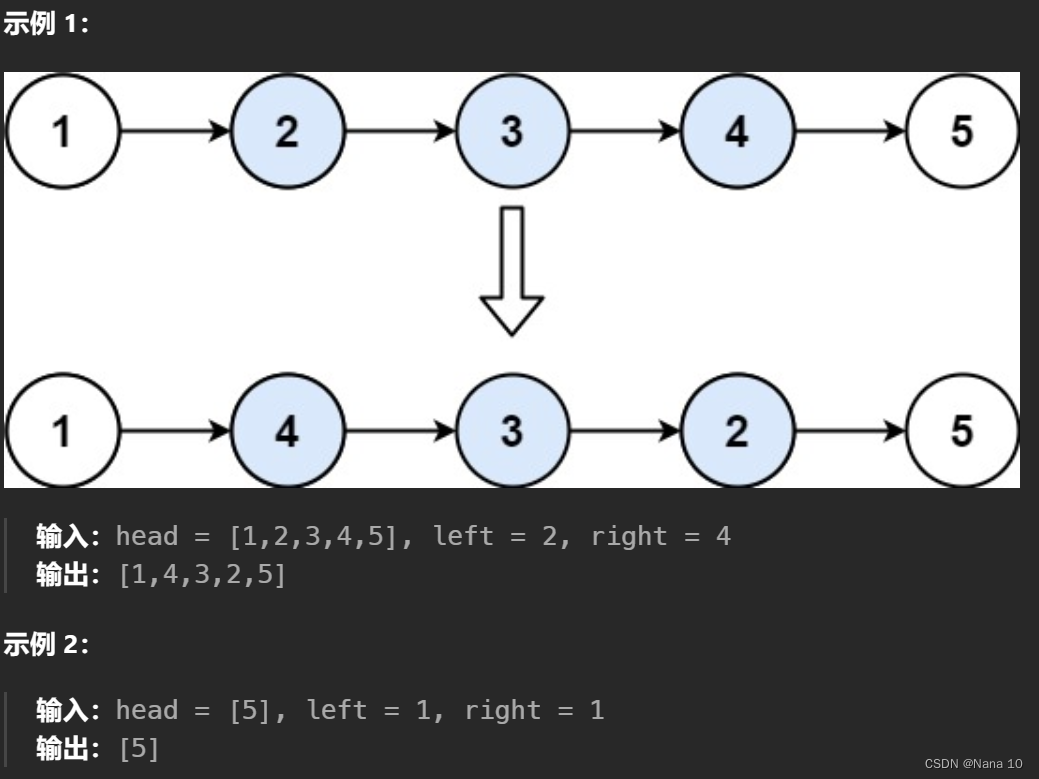
（1）92反转链表–中等

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。
在这里插入图片描述

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
            ListNode* new_head = NULL;
            ListNode* next = head;
            ListNode* pre_head = NULL;
            ListNode* latter_head = NULL;
            ListNode* reversed_first_node = NULL;
            int count = 1;
            while(head){
                if(left == right) return head;
                else if(count < left){
                    pre_head = next;
                    next = next->next;
                    count += 1;
                }
                else if (left <= count && count < right){
                    //逆置的长度如果只有1的话，就不需要逆置
                    //从最左边开始，没有pre_head
                    if(left == count) reversed_first_node = next;
                    if(left != 1) pre_head->next = next->next;
                    else head = next->next;
                    next->next = new_head;
                    new_head = next;
                    if(left == 1) next = head;
                    else next = pre_head->next;
                    count+=1;
                }
                else if (count == right){
                    latter_head = next->next;
                    if (left != 1) pre_head->next = latter_head;
                    next->next=new_head;
                    new_head = next;
                    next = latter_head;
                    //逆置完成，开始拼接
                    if (left != 1) pre_head->next = new_head;
                    reversed_first_node->next = latter_head;
                    break;
                }

            }return head;
    }
};

在这里插入图片描述

（2）160相交链表–简单

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
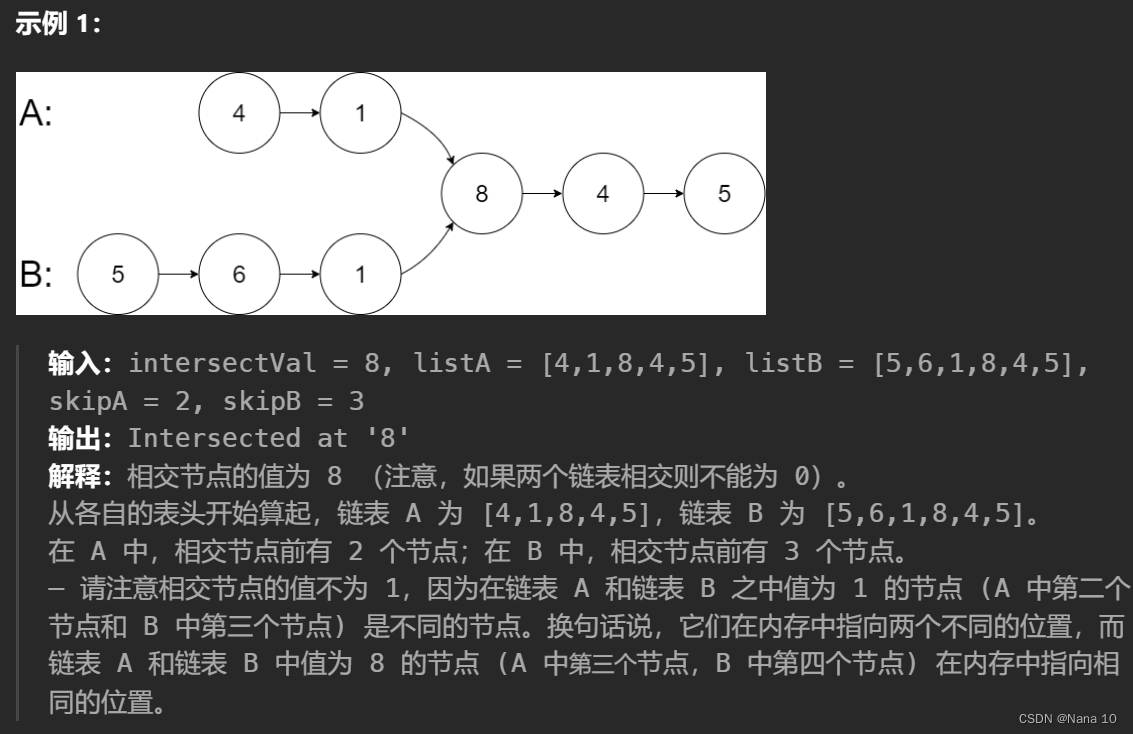
在这里插入图片描述


```cpp
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
#include<iostream>
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        
        if(headA == NULL or headB == NULL) return NULL;
        //_a标志从哪个点开始相同
        //_b标志正在检查哪个点
        ListNode* A_a = headA;
        ListNode* A_b = headA;
        ListNode* B_a = headB;
        ListNode* B_b = headB;
        //计算A和B的长度，方便末端对齐
        int count_A = 1;
        int count_B = 1;
        while(A_a){
            A_a = A_a->next;
            count_A++;
        }
        while(B_a){
            B_a = B_a->next;
            count_B++;
        }

        A_a = headA;
        B_a = headB;

        if(count_A > count_B){
            int len = count_A - count_B;
            while(len){
                A_a = A_a->next;
                len--;
            }A_b = A_a;
        }

        else if(count_A < count_B){
            int len = count_B - count_A;
            while(len){
                B_a = B_a->next;
                len--;
            }B_b = B_a;
        }
        cout<< A_a->val<< endl;
        cout<< B_a->val<< endl;
        //到此，两链表已经末端对齐

        while(A_b){
            //注意，是数值相等，不是指针相等
            if(A_b != B_b){
                A_a=A_b->next;
                A_b=A_b->next;
                B_a=B_b->next;
                B_b=B_b->next;
            }
            else{
                A_b = A_b->next;
                B_b = B_b->next;
            }

        }
        //cout<< A_a->val<< endl;
        return A_a;
    }
};

在这里插入图片描述

（3）142环形链表二–中等

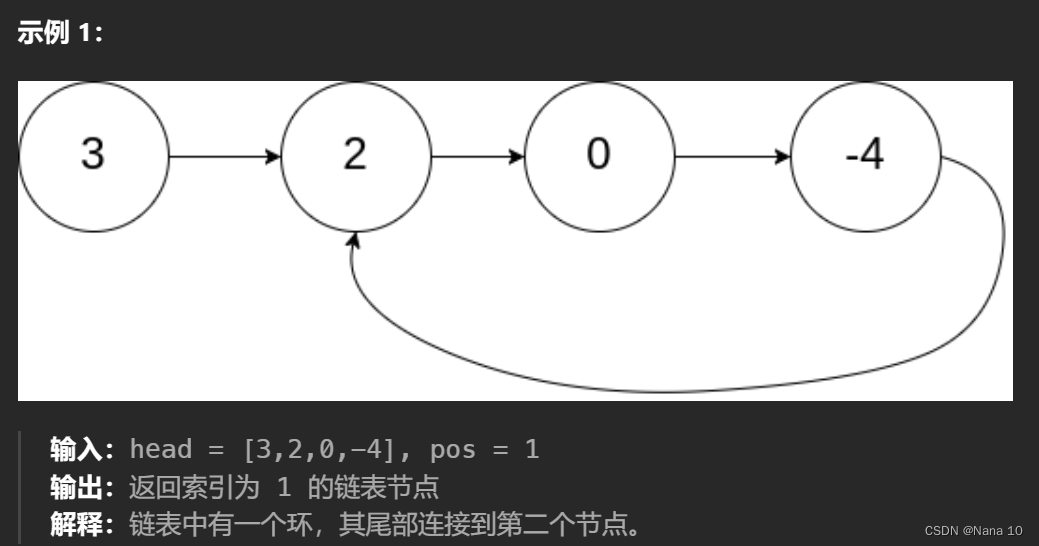
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

在这里插入图片描述

法一：利用集合

#include<iostream>
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        std::set<ListNode*> nodeSet;
        if(head == NULL || head->next == NULL  ) return NULL;
        while(head){
            //cout<< head->val << endl;
            //在集合的非最后一个元素处找到该节点，则说明已经加过该节点，则该点为循环的起始点
            if(nodeSet.find(head) != nodeSet.end())
                return head;
            nodeSet.insert(head);
            head = head->next;
        }return NULL;
    }
};

在这里插入图片描述

法二：快慢指针赛跑

就像跑800，如果有环，快指针肯定能再一次相遇慢指针。
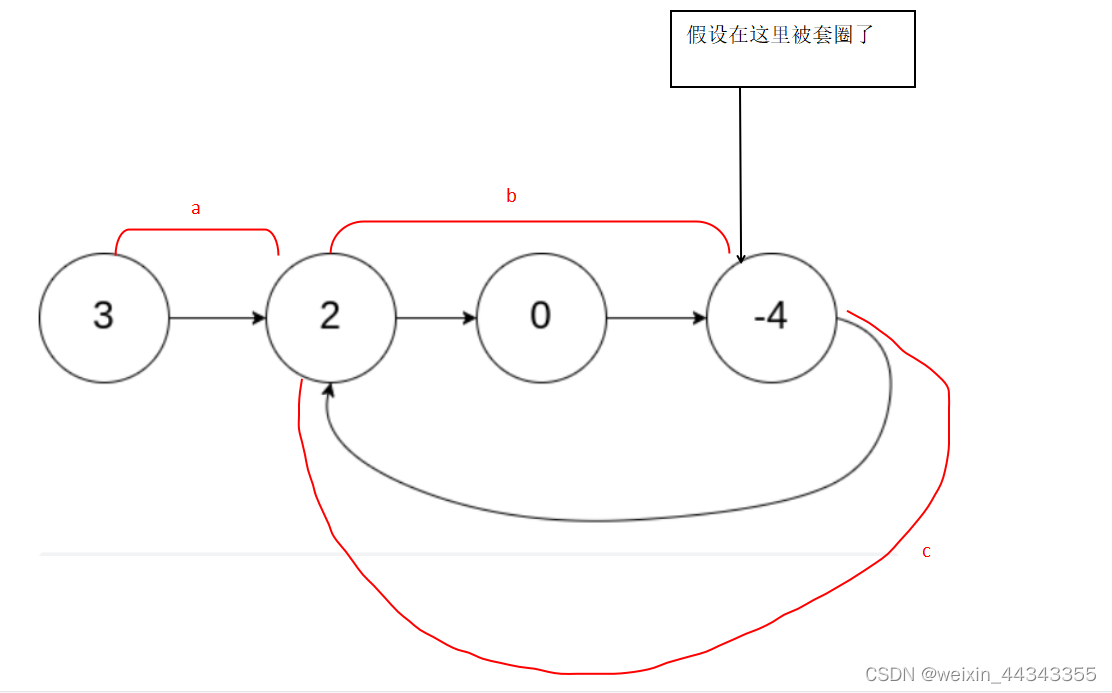
在这里插入图片描述

假设快指针每次走两步，慢指针每次走一步
在相同时间内，快指针走的距离是慢指针的两倍

a：起始点到环开始点的距离
b：环开始点到相遇点的距离
c：相遇点到环开始点的距离

快指针跑过的距离：a+b+c+b
慢指针跑过的距离：a+b

所以，a+b+c+b = 2*(a+b)
即：a = c
也就是说，从开始点和快慢指针相遇点一起开始向前走，一次走一格，如果到达了同一个点，即环开始的点

 #include<iostream>
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == NULL || head ->next == NULL) return NULL;
        //初始点位指向头结点
        ListNode* fastPoint = head->next->next;
        if(fastPoint == NULL) return NULL;
        cout<< fastPoint->val<< endl;
        //fastPoint = ;
        ListNode* slowPoint= head->next;
        //cout<<slowPoint->val<<endl;
        //slowPoint = head;
        while(fastPoint){
            //找到了相遇点就退出循环
            if(slowPoint == fastPoint) break;
            //快指针每次走两步，慢指针每次走一步
            slowPoint = slowPoint ->next;
            if(fastPoint -> next)
                fastPoint = fastPoint -> next -> next;
            else return NULL;
        }
        //cout<<slowPoint->val<<endl;
        if(fastPoint == NULL) return NULL;//如果走到了尽头，则说明没有环
        fastPoint = head;
        //*tmpPoint->next = &head;//tmpPoint回到头，开始以慢指针的速度开始走
        //两指针未相遇，就一直往前走
        while(fastPoint != slowPoint){
            fastPoint = fastPoint->next;
            slowPoint = slowPoint->next;
        }return slowPoint;
    }
};

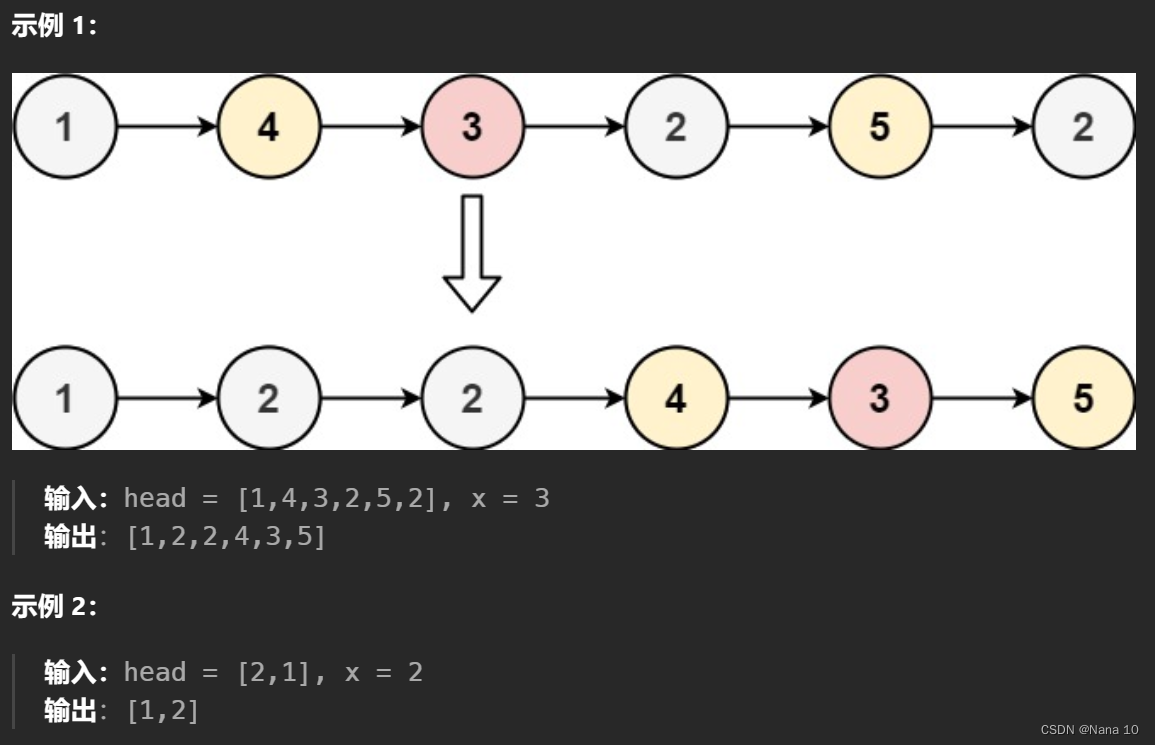
（4）86分隔链表–中等

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。
在这里插入图片描述

class Solution {
public:

    ListNode* partition(ListNode* head, int x) {
        if(head == NULL || head->next ==NULL) return head;
        //设置两个临时头结点
        ListNode lessHead(0);
        ListNode moreHead(0);
        //对应指针分别指向这两个临时头结点
        ListNode* lessptr = &lessHead;
        ListNode* moreptr = &moreHead;
        while(head){
        	//比x大的插入到moreptr后
            if(head->val>= x){
                moreptr->next = head;
                moreptr = head;
            }
            //比x小的插入到lessptr后
            else{
                lessptr->next = head;
                lessptr = head;
            }
            head = head->next;
        }
        //两个链表相连
        lessptr->next = moreHead.next;
        moreptr->next = NULL;
        return lessHead.next;
    }
};

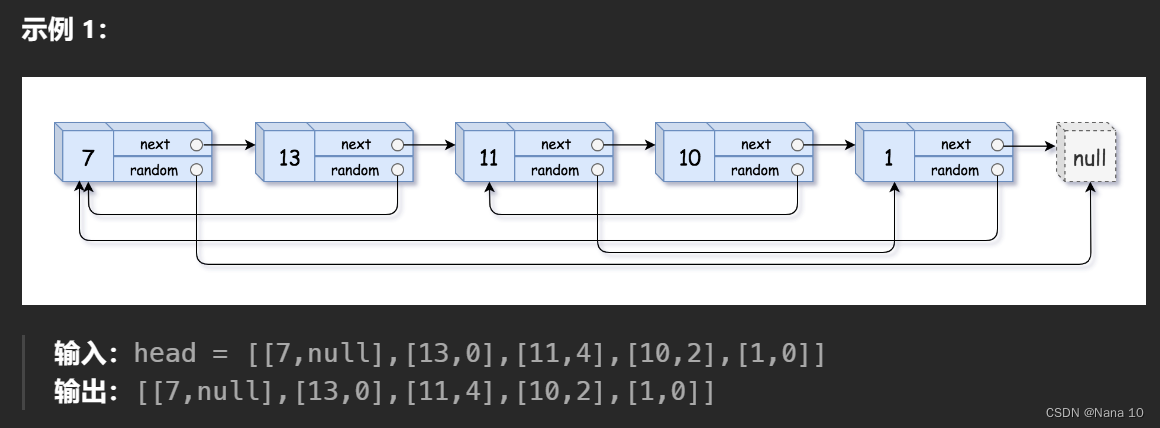
（5）138复制带随机指针的链表–中等

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。

在这里插入图片描述

using namespace std;
class Solution {
public:
    Node* copyRandomList(Node* head) {
        vector<Node*> node_vec;//位置到节点的映射
        map<Node*, int> node_map;//地址到位置的映射
        Node* ptr = head;
        
        int i = 0;
        while(ptr){
            //生成新节点，放入列表
            node_vec.push_back(new Node(ptr->val));
            node_map[ptr] = i;
            i++;
            ptr = ptr->next;
        }
        node_vec.push_back(NULL);
        ptr= head;
        i=0;
        while(ptr){
            //新节点依次相连
            node_vec[i]->next = node_vec[i+1];
            if(ptr->random){
                //通过map，找出random到位置的映射
                int node = node_map[ptr->random];
                node_vec[i]->random = node_vec[node];
            }
            else node_vec[i]->random = NULL;
            ptr = ptr->next;
            i++;
        }
        return node_vec[0];
    }
};

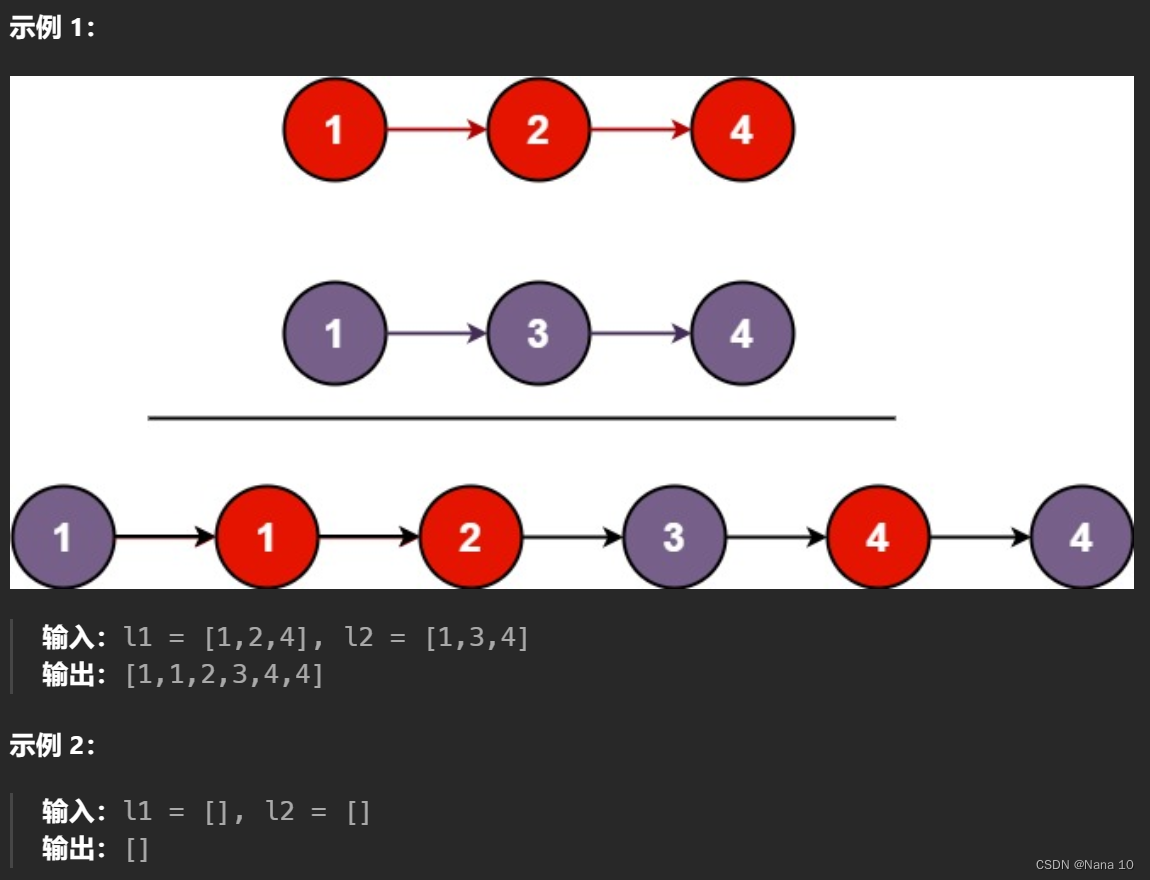
在这里插入图片描述

（6）21合并两个有序链表–简单

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
在这里插入图片描述

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1 == NULL ) return list2;
        if(list2 == NULL ) return list1;
        //设置一个头结点
        ListNode newnode(0);
        //newnode->val = 0;
        ListNode* newnodeHead = &newnode;
        //取两链表头结点，较小者插入新链表
        while(list1&&list2){
            if(list1->val <= list2->val){
                newnodeHead ->next = list1;
                list1 = list1->next;
            }
            else{
                newnodeHead ->next = list2;
                list2 = list2->next;
            }
            newnodeHead = newnodeHead->next;
            newnodeHead->next = NULL;
        }
        //将未空的链表直接接到新链表后
        if(list1 !=NULL){
            newnodeHead->next = list1;
        }
        else if(list2 !=NULL){
            newnodeHead->next = list2;
        }
        return newnode.next;
        }
    };

在这里插入图片描述

（7）23合并k个升序表–困难

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。
在这里插入图片描述
法一、二

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 #include<iostream>
class Solution {
public:
    //自定义比较函数
    //如果不加static
    //非static成员函数在经过编译后编译器会他们添加一个this指针参数
    //变成bool cmp(Solution *this, const ListNode* a,const ListNode*b)
    //而标准库的sort()函数的第三个cmp函数指针参数中并没有这样this指针参数，因此会出现
    //cmp参数和sort()要求的参数不匹配，从而导致：
    //error: reference to non-static member function must be called

    //static静态类成员函数是不需要this指针的，因此改为静态成员函数即可通过
    static bool cmp(const ListNode* a,const ListNode*b){
        return a->val < b->val;
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        //if (lists.size() == 0) return NULL;
        //else if (lists[0] == NULL&& lists.size() == 1) return NULL;
        //假设链表长度为n，有k个链表
        //方式1：链表两两合并
        //时间复杂度为：(n+n)+(2n+n)+...+((k-1)*n+n) = O(k^2*N)=O(kn*k)
        //方式2：放入vector中，将vector排序，再将各个节点相连
        //时间复杂度为：O(kn*logkn)
        //当kn很大的时候，logkn小于k
        vector<ListNode*> points;
        ListNode* ptr = NULL;
        int listsLength = lists.size();
        for(int i = 0; i<listsLength; i++){
            ptr = lists[i];
            while(ptr){
                points.push_back(ptr);
                //cout<<ptr->val<<endl;
                ptr = ptr->next;
                
            }
        }
        if(points.size() == 0) return NULL;
        

        std::sort(points.begin(),points.end(),cmp);

        listsLength = points.size();
        for(int i = 0; i<listsLength-1; i++){
            points[i]->next = points[i+1];
        }points[listsLength-1]->next = NULL;
        return points[0];

        

        
    }
};

在这里插入图片描述

法三：分治

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 #include<iostream>
class Solution {
public:
    //法三，时间复杂度为O(kn*logkn),链表较长时便可看出效率
    ListNode* mergeTowLists(ListNode* a,ListNode*b){
        if(a == NULL) return b;
        if(b == NULL) return a;
        ListNode newhead(0);
        ListNode* ptr = &newhead;
        while(a&&b){
            if(a->val<=b->val){
                ptr->next = a;
                a = a->next;
                ptr = ptr->next;
            }
            else{
                ptr->next = b;
                b= b->next;
                ptr = ptr->next;
            }
        }
        if(a) ptr->next = a;
        else ptr->next = b;
        return newhead.next;
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.size() == 0) return NULL;
        else if (lists.size() == 1) return lists[0];
        else if (lists.size() == 2) return mergeTowLists(lists[0],lists[1]);

        int mid = lists.size()/2;

        vector<ListNode*> sub_list1;
        vector<ListNode*> sub_list2;
        for(int i = 0; i< mid; i++) sub_list1.push_back(lists[i]);
        for(int i = mid; i< lists.size(); i++) sub_list2.push_back(lists[i]);

        ListNode* l1 = mergeKLists(sub_list1);
        ListNode* l2 = mergeKLists(sub_list2);

        return mergeTowLists(l1,l2);

        

        
    }
};

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1008043.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Claude: ChatGPT替代大语言模型

Claude: ChatGPT替代大语言模型

【产品介绍】 Claude是Anthropic推出的类ChatGPT大语言模型&#xff0c;也是一个AI人工智能助理&#xff0c;可以帮助各种行业的用户处理工作&#xff0c;如客户服务、法律、教练、搜索和销售。Claude可以通过聊天界面和API进行访问&#xff0c;能够完成各种对话和文本处理任务…
阅读更多...
计算机二级知识点整理

计算机二级知识点整理

翻到了之前准备计算机二级的笔记&#xff0c;现在给大家分享出来。 一、基本知识&#xff1a; 计算机把完成一条指令所花费的时间称为一个指令周期结构化程序设计强调的是程序的易读性boolean类型不能转为其他基本类型数据表达式是由运算符和运算对象构成的&#xff0c;#不是…
阅读更多...
SimpleCG程序交互操作

SimpleCG程序交互操作

前言 之前所有示例程序都是属于展示型的&#xff0c;只是作为展示板输出使用&#xff0c;不涉及键盘和鼠标的输入交互&#xff0c;下面我们开始接触具有交互功能的程序。 没有交互功能的程序可以满足一定需求,不过大部分的程序是不能脱离交互功能的。程序依据使用者的操作进行相…
阅读更多...
Error response from daemon

Error response from daemon

文章目录 遇到的问题解决方法参考 遇到的问题 当输入下面的指令时 docker pull xxxxxx解决方法 打开/etc/docker/daemon.json文件 vim /etc/docker/daemon.json写入以下内容&#xff1a; {"registry-mirrors":["https://docker.mirrors.ustc.edu.cn"]…
阅读更多...
OpenCV 图像像素运算操作

OpenCV 图像像素运算操作

加法操作详解 加减乘除 #include <opencv2/opencv.hpp>using namespace cv;int main() {Mat image imread("image.jpg");if (image.empty()) {std::cout << "无法加载图像" << std::endl;return -1;}// 加法变换Mat addResult;add(ima…
阅读更多...
mac在vscode编码过程中输入()光标在里面的时候想移出来还得动用左右键很麻烦有什么快捷方法

mac在vscode编码过程中输入()光标在里面的时候想移出来还得动用左右键很麻烦有什么快捷方法

下载vscode插件: 想跳出大括号的时候就可以使用tab直接跳出来就行了
阅读更多...
Buuctf web [SUCTF 2019]EasySQL

Buuctf web [SUCTF 2019]EasySQL

又是一道考察sql注入的题 1、起手试探 &#xff08;主要看看输入什么内容有正确的回显&#xff09; 1 0 1 1 # 发现只有在输入1的情况下有正常的回显,输入0或其他字符都没有回显&#xff0c;所以这题就要尝试堆叠注入了。 ps&#xff1a;&#xff08;如果想尝试其他注入方法…
阅读更多...
带你打穿三层内网-红日靶场七

带你打穿三层内网-红日靶场七

文章目录 前记环境配置web1信息搜集cve-2021-3129redis未授权|ssh密钥后渗透 Win7&#xff08;PC1&#xff09;永恒之蓝 web2docker逃逸 win7&#xff08;PC2&#xff09;|DC 前记 所用工具 msfcsvenomfrp蚁剑冰蝎laravel.pyfscan 注意事项 msf的永恒之蓝每次都需要两次才能…
阅读更多...
VM-Linux基础操作命令

VM-Linux基础操作命令

命令执行的本质&#xff1a; 当输入命令&#xff08;单词&#xff09;后敲击回车的那一刻。它就会立刻到以下图片&#xff0c;变量中的文件中去找对应的可执行文件 此路径又叫环境变量 1.shell命令提示符 默认&#xff1a;[rootlocalhost ~]# root&#xff1a;现已登录的账户名…
阅读更多...
重构优化第三方查询接口返回大数据量的分页问题

重构优化第三方查询接口返回大数据量的分页问题

# 问题描述 用户线上查询其上网流量详单数据加载慢&#xff0c;且有时候数据没有响应全~ 1、经排除是调用第三方数据量达10w条响应会超时&#xff0c;数据没正常返回 2、现有线上缓存分页也是加载慢数据不能正常展示 3、第三方接口返回类似报文jsonj&#…
阅读更多...
基于Yolov8的光伏电池缺陷检测，引入ICCV2023 动态蛇形卷积和独家全网首发多维协作注意模块MCA，实现涨点创新十足

基于Yolov8的光伏电池缺陷检测，引入ICCV2023 动态蛇形卷积和独家全网首发多维协作注意模块MCA，实现涨点创新十足

1.光伏电池缺陷数据集介绍 背景&#xff1a;太阳能作为一种极具吸引力的替代电力能源&#xff0c;太阳能光伏电池&#xff08;即光伏电池&#xff09;是太阳能发电系统的基础&#xff0c;一般情况下&#xff0c;电池中的各类缺陷会直接影响到光伏电池的光电转化效率和使用寿命…
阅读更多...
Mybatis-Genertor逆向工程

Mybatis-Genertor逆向工程

1、导入mybaties插件 <build><plugins><plugin><groupId>org.mybatis.generator</groupId><artifactId>mybatis-generator-maven-plugin</artifactId><version>1.4.2</version><dependencies><dependency>…
阅读更多...
Android Fragment

Android Fragment

基本概念 Fragment是Android3.0后引入的一个新的API&#xff0c;他出现的初衷是为了适应大屏幕的平板电脑&#xff0c; 普通手机开发也会加入这个Fragment&#xff0c; 可以把他看成一个小型的Activity&#xff0c;又称Activity片段&#xff01; 如果一个很大的界面&#xff…
阅读更多...
视频直播点播平台EasyDSS创建用户详细操作来啦！

视频直播点播平台EasyDSS创建用户详细操作来啦！

视频推拉流EasyDSS视频直播点播平台&#xff0c;集视频直播、点播、转码、管理、录像、检索、时移回看等功能于一体&#xff0c;可提供音视频采集、视频推拉流、播放H.265编码视频、存储、分发等视频能力服务。 由于旭帆科技的EasyDSS平台支持新建用户&#xff0c;但新建时用户…
阅读更多...
Python 图片处理笔记

Python 图片处理笔记

import numpy as np import cv2 import os import matplotlib.pyplot as plt# 去除黑边框 def remove_the_blackborder(image):image cv2.imread(image) #读取图片img cv2.medianBlur(image, 5) #中值滤波&#xff0c;去除黑色边际中可能含有的噪声干扰#medianBlur( Inp…
阅读更多...
懒汉式之并发安全问题

懒汉式之并发安全问题

在高并发场景下的懒汉式创建对象&#xff0c;造成ID重复创建&#xff0c;代码见下图&#xff1a; 并发场景下&#xff0c;iDCreator对象并未随类的创建而创建&#xff0c;而是在需要的时候进行创建&#xff0c;导致垃圾回收器可以对其进行回收&#xff0c;从而有可能同一时间戳…
阅读更多...
帮助企业轻松搭建帮助中心-Baklib

帮助企业轻松搭建帮助中心-Baklib

Baklib是一个在线知识管理平台&#xff0c;帮助企业搭建在线产品手册、帮助中心、知识库等&#xff0c;Baklib是一个工具型软件&#xff0c;帮助企业高效快速搭建相关文档内容&#xff0c;轻松进行对外分享。 Baklib起源——目前企业的知识管理现状 存储难 将文档存储在本地与…
阅读更多...
卷积网络：实现手写数字是识别50轮准确率97.3%

卷积网络：实现手写数字是识别50轮准确率97.3%

卷积网络&#xff1a;实现手写数字是识别50轮准确率 1 导入必备库2 torchvision内置了常用数据集和最常见的模型3 数据批量加载4 绘制样例5 创建模型7 设置是否使用GPU8 设置损失函数和优化器9 定义训练函数10 定义测试函数11 开始训练12 绘制损失曲线并保存13 绘制准确率曲线并…
阅读更多...
Xilinx ZYNQ 7000学习笔记五(Xilinx SDK 烧写镜像文件)

Xilinx ZYNQ 7000学习笔记五(Xilinx SDK 烧写镜像文件)

概述 前面几篇讲了ZYNQ7000的启动过程&#xff0c;包括BootRom和FSBL的代码逻辑&#xff0c;其中关于FSBL代码对启动模式为JTAG被动启动没有进行分析&#xff0c;本篇将通过将JTAG的功能和通过Xilinx SDK烧写镜像文件到flash来顺道把FSBL中的JTAG代码部分给讲解下。 1.JTAG …
阅读更多...
springboot+jxls复杂excel模板导出

springboot+jxls复杂excel模板导出

JXLS 是基于 Jakarta POI API 的 Excel 报表生成工具&#xff0c;可以生成精美的 Excel 格式报表。它采用标签的方式&#xff0c;类似 JSP 标签&#xff0c;写一个 Excel 模板&#xff0c;然后生成报表&#xff0c;非常灵活&#xff0c;简单&#xff01; Java 有一些用于创建 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023