Problem - G - Codeforces

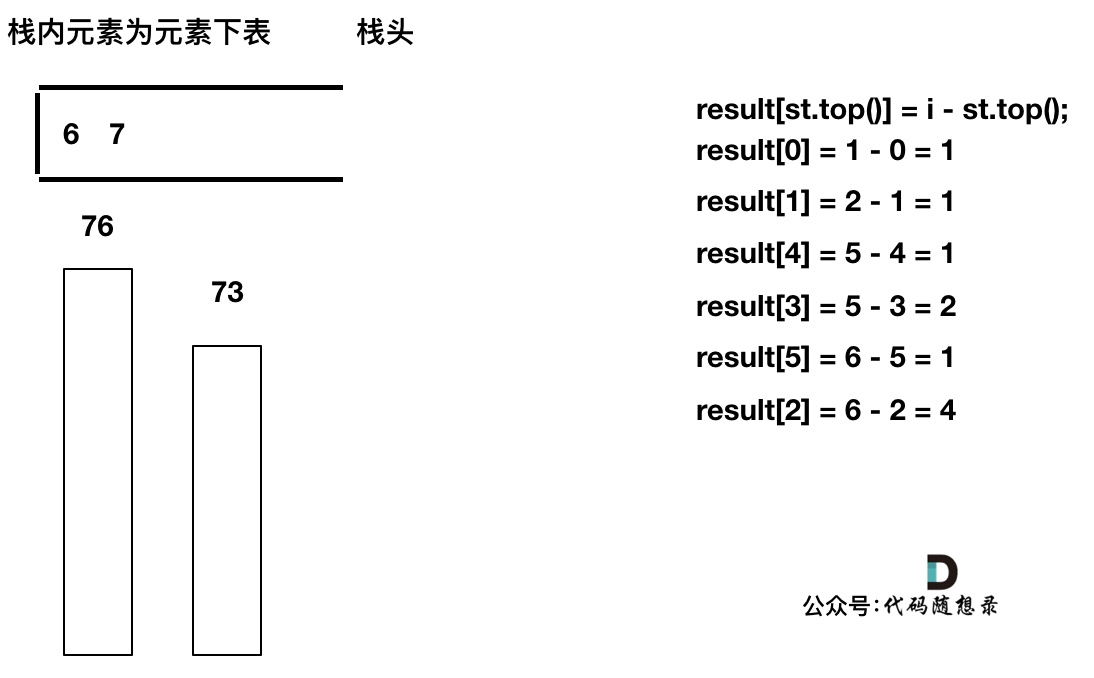
思路：通过它给定的这个操作，我们能够发现操作的本质，在排序后，其实每次操作之后，都会把相邻的两个数的差值减少1，所以最大的操作次数就是相邻的最大的差值，并且这个是可以用set维护出来的，但是知道了最大的差值怎么求出变化后的值一直没想出来，看了题解发现自己很蠢，那么很明显能够发现最大值每次都在加一，那么最后的答案就是相邻的最大差值+在放入平衡器之前的最大值

// Problem: G. The Great Equalizer
// Contest: Codeforces - Codeforces Round 894 (Div. 3)
// URL: https://codeforces.com/contest/1862/problem/G
// Memory Limit: 256 MB
// Time Limit: 4000 ms

#include<bits/stdc++.h>
#include<sstream>
#include<cassert>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7,mod1=998244353;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
int w[N];

void solve() {
	n=read();
	
	for(int i=1;i<=n;i++) w[i]=read();
	
	if(n==1) {
		m=read();
		
		while(m--) {
			int x=read(),c=read();
			printf("%d ",c);
		}
		printf("\n");
		return ;
	}
	
	set<int> s;
	map<int,int> cnt;
	for(int i=1;i<=n;i++) {
		cnt[w[i]]++;
		if(cnt[w[i]]==1) s.insert(w[i]);
	}
	
	priority_queue<int,vector<int>,less<int> > q;
	map<int,int> st;
	
	int last=-1;
	for(auto &it:s) {
		if(last==-1) last=it;
		else {
			int t=it-last;
			q.push(t);
			last=it;
		}
	}
	
	m=read();
	while(m--) {
		int x=read(),c=read();
		
		int k=w[x];
		
		cnt[k]--;
		if(cnt[k]==0) {
			auto it=s.lower_bound(k);
			int tit=*it;
			if(it==s.begin()) {
				int l=*it;
				it++;
				int r=*it;
				st[r-l]++;
			}else {
				auto it1=it,it2=it;
				it1--;
				it2++;
				if(it2==s.end()) {
					int a=*it1,b=*it;
					st[b-a]++;
				}else {
					int a=*it1,b=*it,c=*it2;
					st[b-a]++;
					st[c-b]++;
					q.push(c-a);
				}
			}
			
			s.erase(s.lower_bound(tit));
		}
		
		cnt[c]++;
		w[x]=c;
		if(cnt[c]==1) {
			auto t1=s.lower_bound(c);
			if(t1==s.end()) {
				auto it1=t1;
				it1--;
				int ta=*it1,tb=c;
				q.push(tb-ta);
				s.insert(c);
			}else {
				if(t1==s.begin()) {
					int ta=c,tb=*t1;
					q.push(tb-ta);
					s.insert(c);
				}else {
					auto it1=t1,it2=t1;
					it1--;
					int ta=*it1,tb=c,tc=*it2;
					q.push(tb-ta),q.push(tc-tb);
					st[tc-ta]++;
					s.insert(c);
				}
			}
		}
		
		while(q.size()&&st[q.top()]!=0) {
			st[q.top()]--;
			q.pop();
		}	
		
		auto t=s.rbegin();
		
		int tk=0;
		if(q.size()) tk=q.top(); 
		
		printf("%d ",*t+tk);
	}
	
	printf("\n");
}   

int main() {
    // init();
    // stin();
	// ios::sync_with_stdio(false); 

    scanf("%d",&T);
    // T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}