基础知识

激活函数是神经网络中的一种非线性函数，它作为神经元的输出函数，将输入信号进行转换并引入非线性特性。激活函数的引入能够给神经网络增加更强的表达能力和拟合复杂函数的能力。

在神经网络中，每个神经元都有一个激活函数，它接受输入信号（来自前一层神经元或输入层）并计算输出。激活函数的作用是对输入信号进行非线性变换，从而为神经网络引入非线性能力，使其能够学习和表示更加复杂的数据模式和关系。
类似于人类大脑中基于神经元的模型，激活函数最终决定了是否传递信号以及要发射给下一个神经元的内容。在人工神经网络中，一个节点的激活函数定义了该节点在给定的输入或输入集合下的输出。

Sigmoid函数（Logistic函数）

Sigmoid函数，也称为Logistic函数，是一种常见的激活函数。它将输入的实数映射到一个范围在0到1之间的输出。常用于二分类问题或作为输出层的激活函数。

Sigmoid函数的数学表达式如下：

$\frac{1}{1 + e^{-x}}$

其中，x表示输入值，e是自然对数的底。函数的输出f(x)位于0到1之间。

当x趋近于正无穷大时，f(x)趋近于1；
当x趋近于负无穷大时，f(x)趋近于0。

Sigmoid的函数图像：
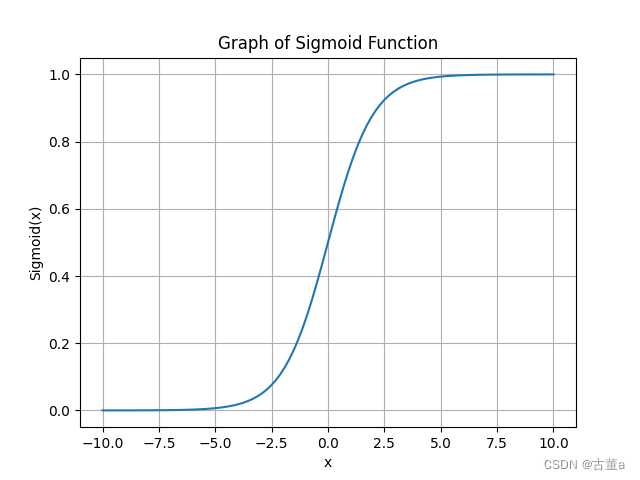
在这里插入图片描述
Sigmoid函数的特点：

它的输出是连续、光滑的，并且具有可导性，这使得在反向传播算法中可以对其进行梯度计算。在神经网络中，Sigmoid函数通常用作二分类问题的输出层激活函数，也可以用作隐藏层的激活函数。
然而，Sigmoid函数在输入值非常大或非常小的情况下，梯度接近于0，这可能导致梯度消失的问题。

Sigmoid函数的代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 生成 x 值
x = np.linspace(-10, 10, 100)

# 计算 Sigmoid(x) 的值
sigmoid = 1 / (1 + np.exp(-x))

# 绘制曲线
plt.plot(x, sigmoid)
plt.title('Graph of Sigmoid Function')
plt.xlabel('x')
plt.ylabel('Sigmoid(x)')
plt.grid(True)
plt.show()

双曲正切函数（Tanh函数）

双曲正切函数是双曲函数的一种。双曲正切函数在数学语言上一般写作tanh ⁡。它将输入的实数映射到一个范围在 -1到1之间的输出，解决了Sigmoid函数的不以0为中心输出问题，然而，梯度消失的问题和幂运算的问题仍然存在。

Tanh函数的数学表达式如下：

$\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$
其中，x表示输入值，e是自然对数的底。函数的输出f(x)位于-1到1之间。

当x趋近于正无穷大时，f(x)趋近于1；
当x趋近于负无穷大时，f(x)趋近于-1。

TanH的函数图像：
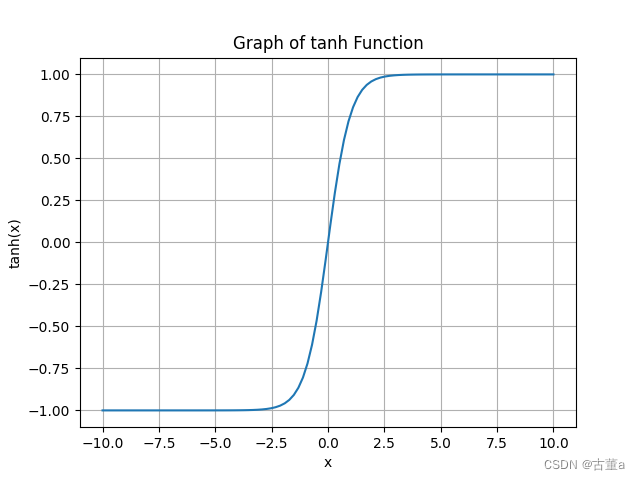
tanh函数图像
TanH函数的代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 生成 x 值
x = np.linspace(-10, 10, 100)

# 计算 tanh(x) 的值
y = np.tanh(x)

# 绘制曲线
plt.plot(x, y)
plt.title('Graph of tanh Function')
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.grid(True)
plt.show()

Tanh函数与Sigmoid函数类似，但相对于Sigmoid函数而言，Tanh函数具有更好的对称性。它可以用作隐藏层的激活函数，能够处理正负值的输入，并保留输入的相对关系。

线性整流函数（ReLU函数）

线性整流函数，又称修正线性单元ReLU，是一种人工神经网络中常用的激活函数，通常指代以斜坡函数及其变种为代表的非线性函数。

ReLU函数的数学表达式如下：

$\max(0, x)$

其中，x表示输入值。

如果输入值x大于0，则ReLU函数返回输入值x本身；
如果输入值x小于或等于0，则ReLU函数返回0。

ReLU的函数图像：
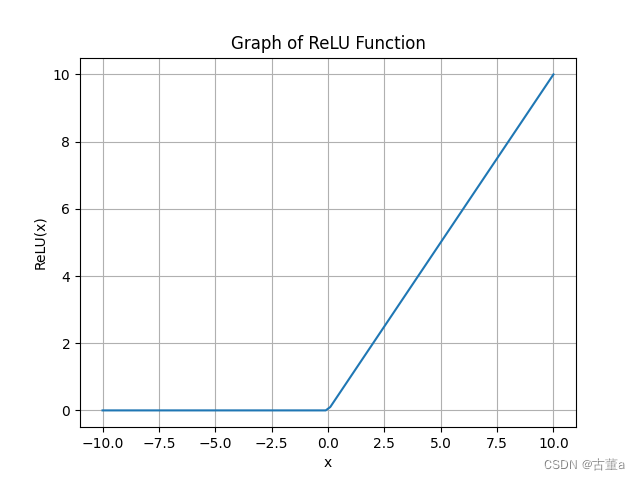
在这里插入图片描述
ReLU函数的代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 生成 x 值
x = np.linspace(-10, 10, 100)

# 计算 ReLU(x) 的值
relu = np.maximum(0, x)

# 绘制曲线
plt.plot(x, relu)
plt.title('Graph of ReLU Function')
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.grid(True)
plt.show()

ReLU函数（线性整流函数）主要特点：

非线性：ReLU函数是一个非线性函数，它在输入值大于0时返回输入值本身，而在输入值小于或等于0时返回0。这种非线性特性使得神经网络能够学习和表示更加复杂的函数关系。
稀疏激活性：当输入值小于等于0时，ReLU函数的输出为0，这意味着对应的神经元将不会被激活。这种稀疏激活性可以使网络具有更高的稀疏性，从而减少参数的冗余性，提高计算效率。
零梯度问题：ReLU函数在输入值大于0时具有常数梯度，这意味着在正区间内梯度保持为1。这样的特性可以加速梯度下降的收敛速度，并减轻梯度消失的问题。
线性可分性：ReLU函数能够将输入值划分为两个线性可分的区域，即正区间和负区间。这种线性可分性使得ReLU函数在处理线性可分问题时表现良好。
异常值不敏感：ReLU函数对于大于0的输入值不受异常值的影响。即使输入值非常大，ReLU函数的输出仍然是一个正数，从而减轻了异常值的影响。

Leaky ReLU函数

Leaky ReLU函数是对ReLU函数的一种改进，旨在解决ReLU函数中的神经元死亡问题（Dead ReLU）。

Leaky ReLU函数的数学表达式：

$\begin{cases} ax, & \text{if } x < 0 \\ x, & \text{if } x \geq 0 \end{cases}$

其中，x表示输入值，a是一个小于1的常数，通常取0.01。

如果输入值x大于0，Leaky ReLU函数返回输入值x本身；
如果输入值x小于等于0，Leaky ReLU函数返回输入值ax。

与ReLU函数不同的是，Leaky ReLU函数在负区间中引入了一个小的斜率，使得神经元在负区间也能具有非零的梯度。

Leaky ReLU的函数图像：

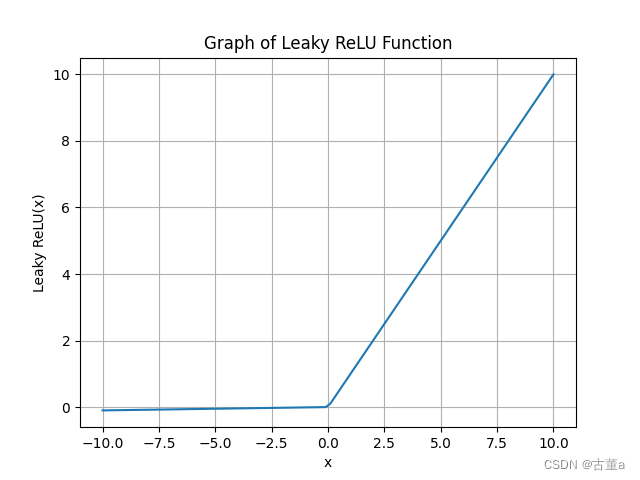
在这里插入图片描述
Leaky ReLU函数的代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 定义Leaky ReLU函数
def leaky_relu(x, a):
    return np.maximum(a * x, x)

# 生成 x 值
x = np.linspace(-10, 10, 100)

# 定义斜率
a = 0.01

# 计算 Leaky ReLU(x) 的值
leaky_relu_vals = leaky_relu(x, a)

# 绘制曲线
plt.plot(x, leaky_relu_vals)
plt.title('Graph of Leaky ReLU Function')
plt.xlabel('x')
plt.ylabel('Leaky ReLU(x)')
plt.grid(True)
plt.show()

Leaky ReLU函数（带泄露的线性整流函数）主要特点：

非线性：Leaky ReLU函数是一个非线性函数，可以处理非线性的函数关系。
解决神经元死亡问题：Leaky ReLU函数引入了一个小的斜率（通常取较小的正数，如0.01），使得神经元在负区间也能具有非零的激活。这有助于避免神经元完全不激活的问题，称为神经元死亡。
具有稀疏激活性：当输入值小于0时，Leaky ReLU函数的输出为一个小的斜率乘以输入值，这意味着对应的神经元在负区间仍然得到一定程度的激活。这种稀疏激活性可以使网络具有更高的稀疏性，减少参数的冗余性。
缓解梯度消失问题：Leaky ReLU函数在负区间具有非零的梯度，这有助于减轻梯度消失问题。相比于ReLU函数的常数梯度，Leaky ReLU函数的斜率可调，可以在一定程度上保持梯度的传播，提高网络的学习能力。
异常值不敏感：与ReLU函数类似，Leaky ReLU函数对于大于0的输入值不受异常值的影响。即使输入值非常大，Leaky ReLU函数的输出仍然是一个正数。

Softmax函数

Softmax函数是一种常用的激活函数，通常用于多分类问题中。它将一组实数转化为表示概率分布的向量。

Softmax函数的数学表达式：

$\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{N} e^{x_j}}$

Softmax函数图像：
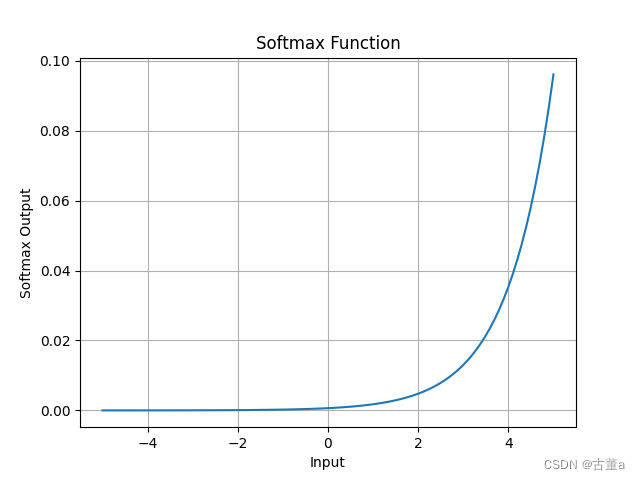
在这里插入图片描述

Softmax函数的代码实现：

import numpy as np
import matplotlib.pyplot as plt

def softmax(x):
    e_x = np.exp(x)
    return e_x / np.sum(e_x)

# 定义输入向量
x = np.linspace(-5, 5, 100)

# 计算Softmax函数的输出
y = softmax(x)

# 绘制Softmax函数图像
plt.plot(x, y)
plt.xlabel('Input')
plt.ylabel('Softmax Output')
plt.title('Softmax Function')
plt.grid(True)
plt.show()