层序遍历(一)

题目

思路

代码

层序遍历(二)

题目

思路

代码

根据二叉树创建字符串

题目

思路

代码

二叉树的最近公共祖先

题目

思路

代码

暴力版

队列版

栈版

bs树和双向链表

题目

思路

代码

前序中序序列构建二叉树

题目

思路

代码

中序后序序列构建二叉树

题目

思路

代码

非递归前序遍历

题目

思路

代码

非递归中序遍历

题目

思路

代码

非递归后序遍历

题目

思路

代码

层序遍历(一)

题目

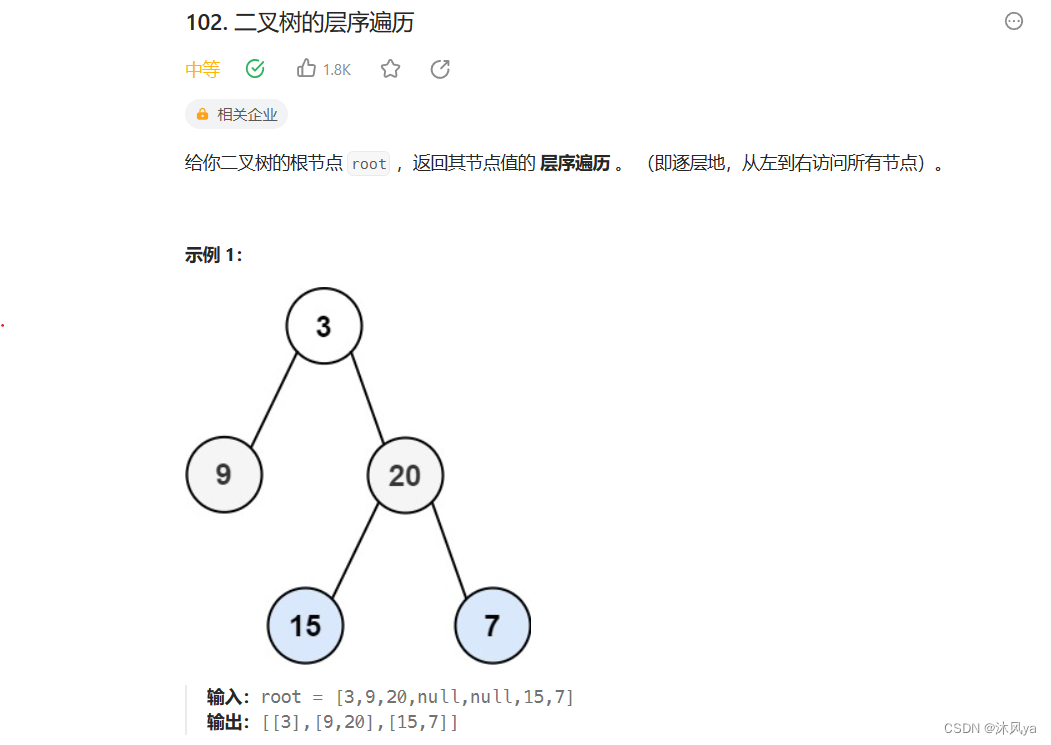
102. 二叉树的层序遍历 - 力扣（LeetCode）

思路

之前写过层序遍历,思路就是用队列存储结点,每次出一层,然后入出的结点的子结点

重点就是要记录一层的结点个数,然后出相应个数的结点

代码

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> arr;
        queue<TreeNode*> q;
        if(root!=nullptr){
            q.push(root);
        }
        while(!q.empty()){
            vector<int> tmp; //存储一层的结点
            int size=q.size(); //此时队列内的元素就是上一层的结点个数
            for(int i=0;i<size;++i){
                tmp.push_back(q.front()->val);
                if(q.front()->left){ //有子树就放进队列中
                    q.push(q.front()->left);
                }
                if(q.front()->right){
                    q.push(q.front()->right);
                }
                q.pop(); //出掉这个父结点
            }
            arr.push_back(tmp);
        }
        return arr;
    }

层序遍历(二)

题目

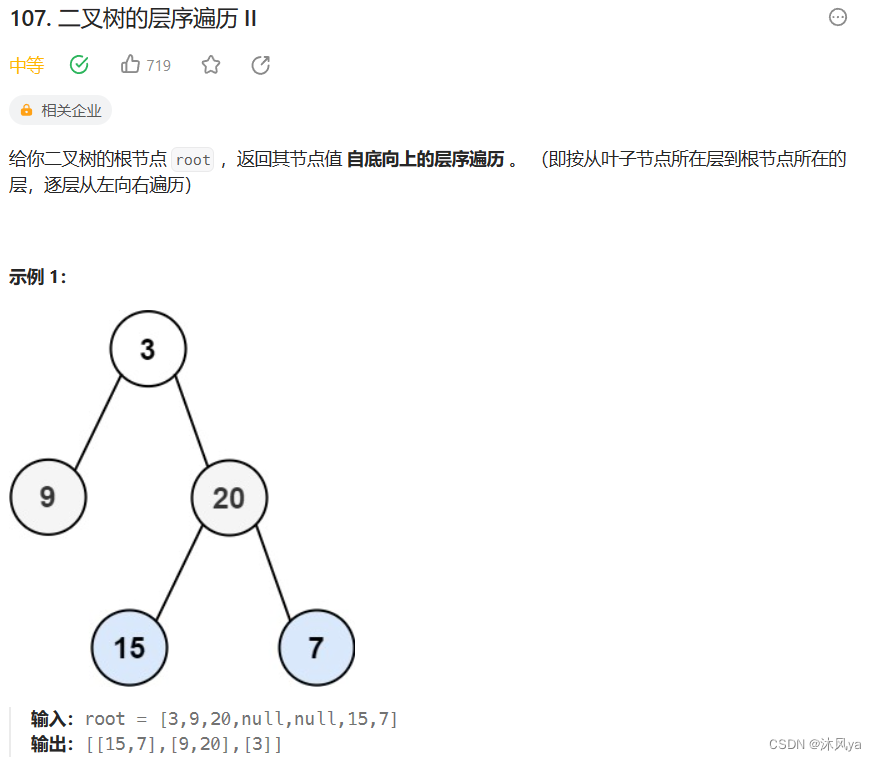
107. 二叉树的层序遍历 II - 力扣（LeetCode）

思路

看似好像很麻烦,其实只要把上一道题得到的答案逆置就行了

代码

    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> arr;
        queue<TreeNode*> q;
        if(root!=nullptr){
            q.push(root);
        }
        while(!q.empty()){
            vector<int> tmp;
            int size=q.size();
            for(int i=0;i<size;++i){
                tmp.push_back(q.front()->val);
                if(q.front()->left){
                    q.push(q.front()->left);
                }
                if(q.front()->right){
                    q.push(q.front()->right);
                }
                q.pop();
            }
            arr.push_back(tmp);
        }
        reverse(arr.begin(),arr.end());  //逆置
        return arr;
    }

根据二叉树创建字符串

题目

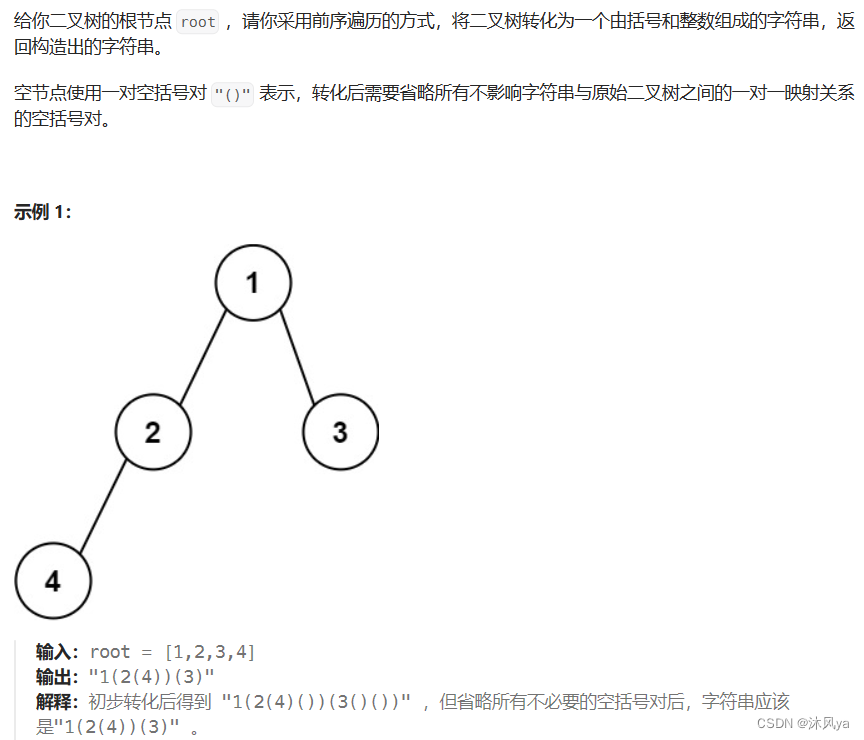
606. 根据二叉树创建字符串 - 力扣（LeetCode）

思路

基础代码还是一个前序遍历,只不过需要在打印时需要好好处理一下

首先,不能有不必要的括号,比如有左树无右树 / 左右子树全无
但是要注意,当无左树有右树时,需要将左树的空括号打印出来

代码

    void front_order(TreeNode* root,string& ans){
        if(root==nullptr){
            return ;
        }
        ans+=to_string(root->val);
        if(root->left||root->right){ 
    //左需要特殊判断,左右均有/只有右/只有左,都需要打印左,即使是空括号
            ans+='(';
            front_order(root->left,ans);
            ans+=')';
        }
        if(root->right){ //右只需要在它存在时打印
            ans+="(";
            front_order(root->right,ans);
            ans+=')';
        }
    }
    string tree2str(TreeNode* root) {
        string ans;
        front_order(root,ans);
        return ans;
    }

二叉树的最近公共祖先

题目

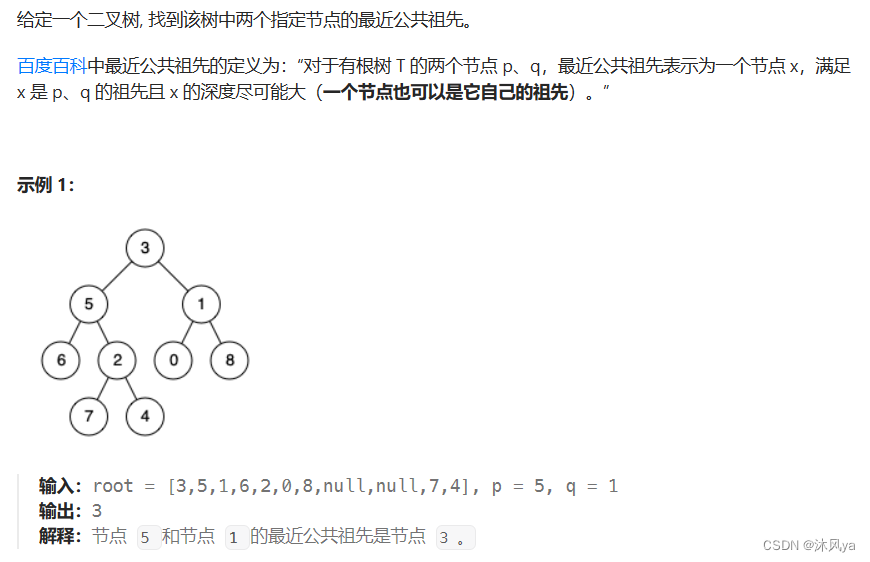
236. 二叉树的最近公共祖先 - 力扣（LeetCode）

思路

如果要找的两个结点分别在某一结点的左右,说明该结点就是公共结点
如果两个结点都在某结点的左子树,那么该结点不会是公共结点,且确定公共结点需要在该结点的左子树中寻找 ; 右子树同理
如果某结点就是要找的两个结点的其中一个结点

除了直接找结点位置,也可以将结点路径存储起来,然后按照找相交链表的交点那样(先从尾巴出[相差个数]个结点),找出公共结点

队列/栈储存都是一样的

代码

暴力版

    bool find(TreeNode* root, TreeNode* p){
        if(root==nullptr){
            return false;
        }
        if(root==p){
            return true;
        }
        return find(root->left,p)||find(root->right,p); //只要一边找到了就返回真
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr){
            return nullptr;
        }
        if(root==p||root==q){
            return root;
        }
        //判断当前结点下,要找结点的相对位置
        bool pleft=find(root->left,p);
        bool pright=!pleft;
        bool qleft=find(root->left,q);
        bool qright=!qleft;
        //如果都在左,去左找
        if(pleft&&qleft){
            return lowestCommonAncestor(root->left,p,q);
        }
        //如果都在右,去右找
        else if(pright&&qright){
            return lowestCommonAncestor(root->right,p,q);
        }
        //走到这里,说明一左一右
        else{
            return root;
        }
    }

队列版

 bool find_q(TreeNode* root, TreeNode* p,queue<TreeNode*>& ans){
        if(root==nullptr){
            return false;
        }
        if(root==p){ 
            ans.push(root); //队列:先入子结点,保证先出的是子结点
            return true;
        }
        if(find_q(root->left,p,ans)){ //为真就存储起来(说明当前结点是路径上的一点)
            ans.push(root);
            return true;
        }
        if(find_q(root->right,p,ans)){ //同理
            ans.push(root);
            return true;
        } 
        return false; //走到这里,说明左右均没找到,就说明这条路没有要找的结点
    } 
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        queue<TreeNode*> sp,sq;
        find_q(root,p,sp);
        find_q(root,q,sq);
        //先将多的出掉
        while(sp.size()>sq.size()){
            sp.pop();
        }
        while(sp.size()<sq.size()){
            sq.pop();
        }
        //然后同时出,直到找到那个公共结点
        while(sp.front()!=sq.front()){
            sp.pop();
            sq.pop();
        }
        return sp.front();
    }

栈版

    bool find_s(TreeNode* root, TreeNode* p,stack<TreeNode*>& ans){
        if(root==nullptr){
            return false;
        }
        ans.push(root); //注意:栈必须得先入父结点,保证先出的是子结点
        if(root==p){
            return true;
        }
        if(find_s(root->left,p,ans)){
            return true;
        }
        if(find_s(root->right,p,ans)){
            return true;
        }
        ans.pop();
        return false;
    }
    
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> sp,sq;
        find_s(root,p,sp);
        find_s(root,q,sq);
        while(sp.size()>sq.size()){
            sp.pop();
        }
        while(sp.size()<sq.size()){
            sq.pop();
        }
        while(sp.top()!=sq.top()){
            sp.pop();
            sq.pop();
        }
    }

bs树和双向链表

题目

二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)

思路

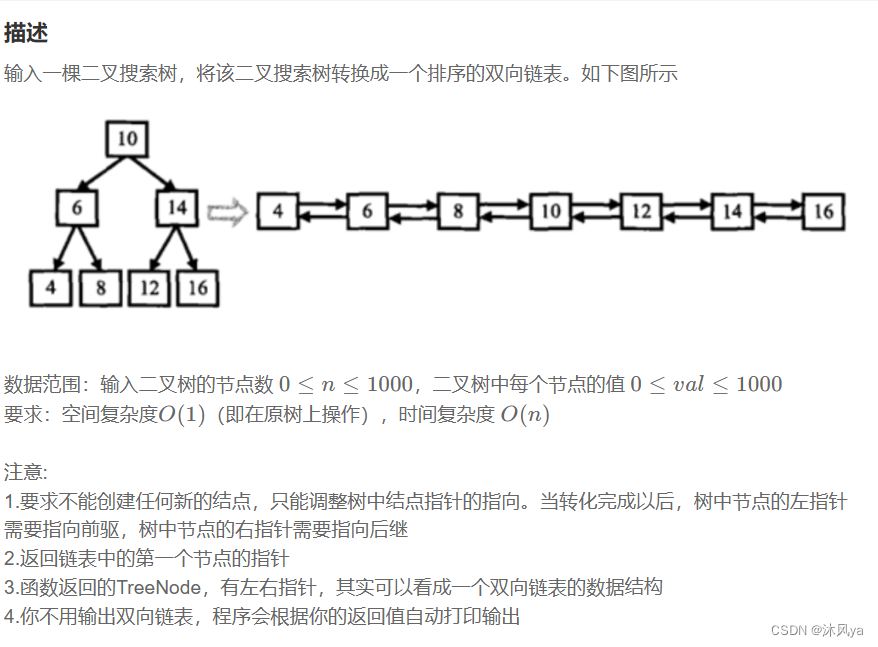
仔细看转化后的双向链表,结点顺序其实就是中序遍历的结点顺序

所以这道题的代码就是在中序遍历的基础上进行处理

因为需要指向前驱和后继,所以至少得搞一个变量,存上一个结点
(毕竟没法知道下一个结点是啥,但上一个还是可以的,就像之前拿到父结点那样)
那么前驱搞定了,后继呢?
其实知道后继也可以,只要穿越到未来,再回到过去就可以知道了
所以,我们实际上知道的后继是上一个结点的,也就是当前结点 (当前结点就是上一个结点的后继)
还要注意一点,我们找到的第一个结点是最左端的,所以它没有前驱
所以首次传入的prev是空指针(prev赋值给结点的前驱)

代码

	void inorder(TreeNode* root,TreeNode*& prev){
		if(root==nullptr){
			return;
		}
		inorder(root->left,prev);
		root->left=prev;
		if(prev){ //prev会为空,所以需要判断,不然就越界了
			prev->right=root;
		}
		prev=root; //因为之后要进root的后继结点了,所以需要更新prev
		inorder(root->right,prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {
		if(pRootOfTree==nullptr){
			return nullptr;
		}
		TreeNode *prev=nullptr,*tmp=pRootOfTree;
		while(tmp->left!=nullptr){ //拿到链表的第一个结点
			tmp=tmp->left;
		}
		inorder(pRootOfTree,prev);
		return tmp;
    }

前序中序序列构建二叉树

题目

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

思路

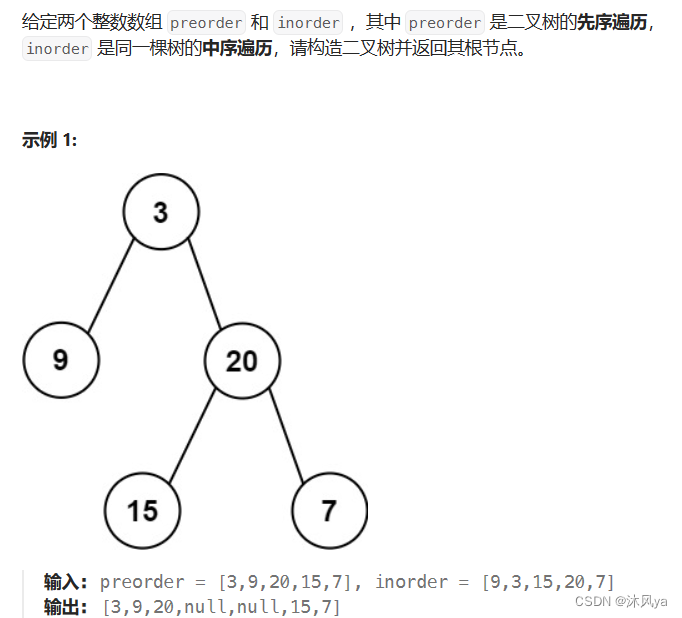
和手动构建树的顺序一样,前序确定根,中序确定根的左右子树,只不过需要用代码写出来

因为每次都需要将中序数组分成两个(是不是很像快排里面的操作),所以我们还是使用递归来写
但要注意,我们还需要一个不断增加的下标来访问前序(中序需要使用两个下标作为范围,它直接传值就行)

代码

class Solution {
public:
    TreeNode* _build(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend) {
        if (inbegin > inend) { //数组不合法,说明不存在这个结点,所以返回空
            return nullptr;
        }
        TreeNode* node = new TreeNode(preorder[prei]); //按照前序构建二叉树(因为先拿到的都是根结点)
        int begin = inbegin;
        // while(preorder[prei]!=inorder[begin]&&begin<=inend){
        //     begin++;
        // }
        for (; begin <= inend; ++begin) { //在中序中找到根结点
            if (preorder[prei] == inorder[begin]) {
                break;
            }
        }
        ++prei; //拿到下一个结点
        node->left = _build(preorder, inorder, prei, inbegin, begin - 1);//在找到的根结点,左区间是左子树
        node->right = _build(preorder, inorder, prei, begin + 1, inend);//同理
        return node;//左右子树构建完毕后,返回该结点
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int prei = 0, inbegin = 0, inend = inorder.size();
        TreeNode* root = _build(preorder, inorder, prei, 0, (int)inorder.size() - 1);
        //注意这里的prei是引用
        return root; //最后返回的就是根结点
    }
};

中序后序序列构建二叉树

题目

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

思路

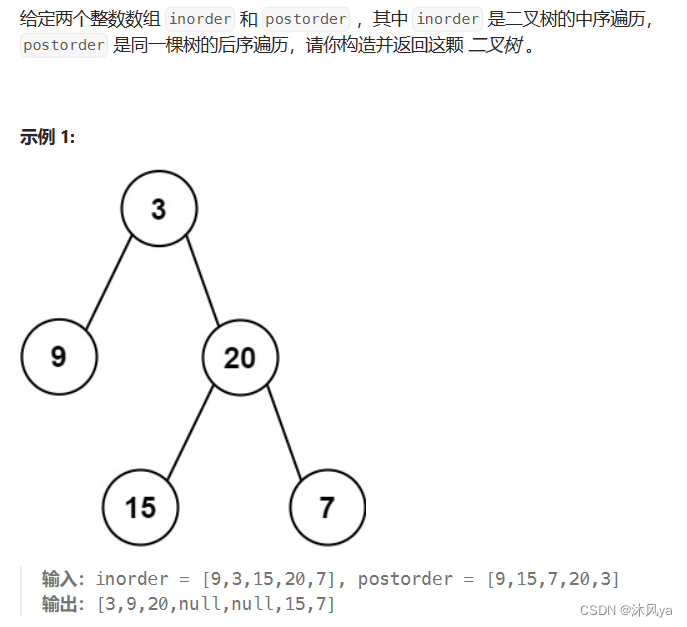
大体思路和上一道题一样,只不过是用后序找根

而且要注意后序是左右根的顺序
后序序列往左走,先找的是右子树的根,所以要先去中序的右半范围寻找

代码

TreeNode* _build(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin,int inend){
        if(inbegin>inend){
            return nullptr;
        }
        TreeNode* root=new TreeNode(postorder[posti]);
        int begin=inbegin;
        while(begin<=inend){
            if(postorder[posti]==inorder[begin]){
                break;
            }
            begin++;
        }
        --posti;  //注意是--嗷
        root->right=_build(inorder,postorder,posti,begin+1,inend);//先被构建的是右子树
        root->left=_build(inorder,postorder,posti,inbegin,begin-1);
        return root;
}
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int posti=postorder.size()-1;
        TreeNode* root=_build(inorder,postorder,posti,0,inorder.size()-1);
        return  root;
    }

非递归前序遍历

题目

144. 二叉树的前序遍历 - 力扣（LeetCode）

思路

虽然是非递归,但思路和递归一样,只不过得用循环做

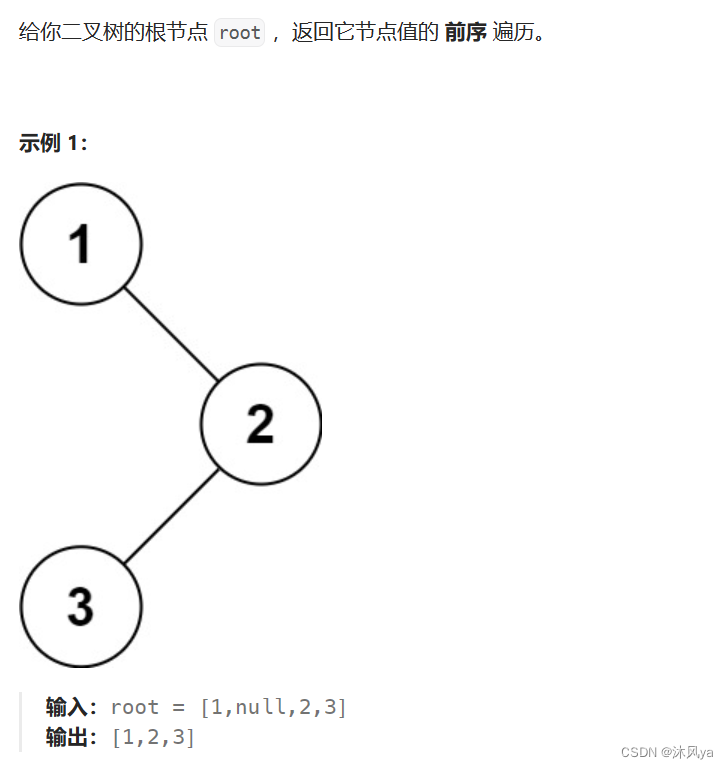
前序是根左右
也就是说,前序的前几个元素都是左方结点
之后开始访问右子树(按照左方节点的倒序)
所以,倒序 -- 不就是栈吗,先入后出!!
所以要用一个栈来存放左结点,然后不断取栈顶+访问其右子树

代码

vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;  //存放前序序列的结点值
        stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树
        TreeNode* cur=root;
        while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环
            while(cur){
                ans.push_back(cur->val); //入左结点
                tmp.push(cur); //存左结点指针
                cur=cur->left;
            }
            TreeNode* top=tmp.top(); 
            cur=top->right; //访问右子树
            tmp.pop();
        }
        return ans;
    }

非递归中序遍历

题目

94. 二叉树的中序遍历 - 力扣（LeetCode）

思路

和前序的思路差不多,但是要注意,中序是左根右

所以需要将左结点先存入栈中(先不要访问!!!)
然后按照栈中顺序,取出,访问
然后,将拿出结点的右结点按照上述操作重复进行,直到遍历完整棵树

代码

    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;  //存放中序序列的结点值
        stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树
        TreeNode* cur=root;
        while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环
            while(cur){ //把所有左结点入栈
                tmp.push(cur);
                cur=cur->left;
            }
            cur=tmp.top();  //拿取栈顶元素
            ans.push_back(cur->val); //入中序序列

            cur=cur->right; //访问其右子树
            tmp.pop(); //该结点没啥用了,直接出
        }
        return ans;
    }

非递归后序遍历

题目

145. 二叉树的后序遍历 - 力扣（LeetCode）

思路

后序是左右根
也就是说,要先遍历完左结点,以及右结点后,才能访问结点
而且要注意,如果该结点有右子树,就需要先循环右子树
但是当循环完成后需要返回来访问结点
该如何判断此时到底该访问右子树还是访问自己呢?
想一想,当上一个结点是其右结点时,不就是该访问自己的时候吗?
而上一个结点是左结点时,是该访问右子树的时候了
所以需要拿到父结点,然后进行判断

代码

    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;  //存放中序序列的结点值
        stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树
        TreeNode* cur=root,*prev=nullptr; 
        while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环
            while(cur){ //把所有左结点入栈(cur就用于把当前结点的左结点存入栈)
                tmp.push(cur);              
                cur=cur->left;
            }
            TreeNode* top=tmp.top(); //代表当前的根结点
            if(top->right==nullptr || top->right==prev){
                ans.push_back(top->val); //入后序序列
                prev=top; //用于下一次循环时,判断上一个结点的右子树是否被访问过
                tmp.pop(); //该结点没啥用了,直接出
            }
            else{
                cur=top->right; //没有被访问过,就去右子树进行循环
            }
        }
        return ans;
    }