C++算法进阶系列之倍增算法解决求幂运算

1. 引言

学习倍增算法，先了解什么是倍增以及倍增算法的优势。如果面前有一堆石子，要求计算出石子的总数量。

这是一个简单的数数问题，可以：

一颗石子一颗石子的数。
两颗石子两颗石子的数。
三颗石子三颗石子的数。
或者更多颗石子更多颗石子的数……

在石子很多的情况下，每一次选择更多石子的方式数，毫无疑问可以快速得到最后的结果，倍增算法便是基于这种数数的理念。

但是，倍增算法不是以固定的数量来数，而是以 2 的倍数来数，如先数2个、再数 4个、再数8个……这种等比数列的方式递增前进。

为什么选择 2 的倍数递增？

于底层逻辑而言，计算机使用二进制存储数据，计算机处理十进制数字时，会把数字转换成二进制形式。

如十进制 17 的二进制为 10001，以 2 为底数展开为 1X2⁴+0X2³+0X2²+0X2¹+1X2⁰=1X16+0X8+0X4+0X2+0X1。如果不考虑0和1的系数，任何一个表达式都可以表示抽象成形如1+2+4+8+16……的样子，也就是任何一个数字都可以表示成 2 的倍数累加。

如 17=16+1；13=8+4+1；……

倍增算法常用于快速幂、求LCA（最近公共祖先）、O(1)求区间极值、求后缀数组……等一系列问题。倍增思想的核心就是通过预处理规模为幂次大小的子问题，然后将原始问题看作成这些子问题的合并。

2. 快速幂

快速幂的问题并不复杂，但是可以帮助我们理解倍增算法的基本思想。

问题描述：

假如要求aⁿ(a的n次幂)，n可以是一个较大的正整数。此题本质是累乘问题，即进行n次乘a的计算，时间复杂度是O(n)级别的。如下代码使用暴力方案实现累乘过程。

#include <iostream>
using namespace std;
int main(int argc, char** argv) {
	int a,n;
	cin>>a>>n;
	//初始化累乘结果 
	int res=1;
	for(int i=0;i<n;i++){
		res*=a;
	}
	cout<<res<<endl;
	return 0;
}

居于对求幂运算的数学运算法则的认知，根据其法则，可以改善方案，提升性能。

2.1 转换一

可以对 aⁿ 进行如下转换：

当 n 为偶数时， aⁿ=(a^n/2)²。
当 n 为奇数时， aⁿ=(a^n/2)²*a^n%2。

转换法则是典型的递归套路，如下代码是使用递归算法的具体实现。

#include <iostream>
using namespace std;
long long int ksm(int  a,int n) {
	long long int ans=1;
	if(a==1)return 1;
	if(n==1)return a;
	ans=ksm(a ,n/2);
	ans*=ans;
	if(n%2==1) //如果是奇数
		ans*=a;
	return ans;
}
int main(int argc, char** argv) {
	int a,n;
	cin>>a>>n;
	long long int ans=ksm(a,n);
	cout<<ans;
	return 0;
}

现分析一下上述实现的时间复杂度。

现假设 a=2,n=10，其递归调用过程如下图所示。

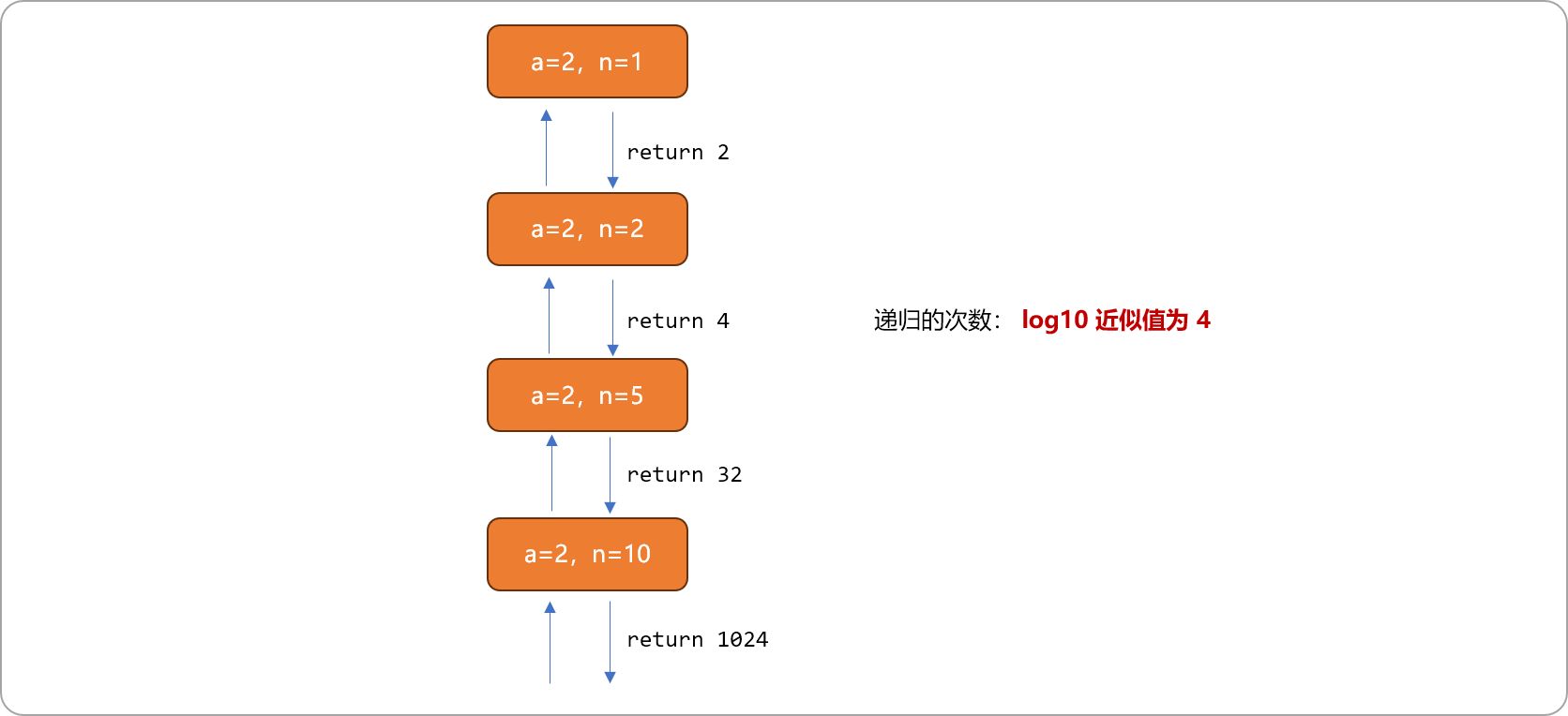
递归算法的时间复杂度计算公式：基函数的时间复杂度X递归的深度。ksm函数的时间复杂度为O(1)，递归次数为logn，最终时间复杂度为O(logn)。递归调用过程中，回溯结果都是以 2 的幂次方返回。

2.2 转换二

假设 a=2,n=10，因为10的二进制1010，所以，a¹⁰ 可以写成 a¹⁰¹⁰，而 1010=1X2³+0X2²+1X2¹+0X2⁰。故 a¹⁰ 也可以写成 a^{1X2³+0X2²+1X2¹+0X2⁰} ，根据幂运算法则： a^{1X2³+0X2²+1X2¹+0X2⁰} = a^1X2³ * a^0X2²* a^1X2¹* a^0X2⁰=a⁸*a²。

为了研究这个表达式的通用含义，假设 n=255，其二进制值为 11111111 ，目的是抛开 0和1系数的干扰抽象出通用表达式，便于寻找其规律：

a²⁵⁵=*a¹²⁸*a⁶⁴*a³² *a¹⁶*a⁸*a⁴*a²*a¹ ；

抽象出来的表达式本质还是累乘操作，累乘的次数由 n 转化为二进制后的位数决定。如 n=255 ，二进制位数为8，累乘次数即为 8，其结果为 log255的值。如果是暴力迭代相乘，a²⁵⁵ 需要迭代255次，幂化后的表达式，迭代只需要8次，时间复杂度由原来的 O(n)提升到了O(logn)。

在整个累乘表达式中，且满足如下的迭代关系：

a¹=a。
a²=a¹*a¹。
a⁴=a²*a²。
a⁸=a⁴*a⁴。
……
a¹²⁸=a⁶⁴*a⁶⁴。

抽象化表达式时，选择了一个很特殊的数字 255，迭代 8 次，且最终结果是这 8 次迭代的累乘。如果 n=10，其二进制为 1010，转换后的表达式应该为a¹⁰= a⁸ * a²，需要漏掉 a¹和a⁴的值。

根据前面的迭代推导关系，a⁸ 的值由 a⁴决定，虽然 a⁴ 的值不是最终结果中的一部分，但是推导过程不能省略。

其求值过程应该如下：

求解出 a¹的值: a¹=a。因为 1010的最后一位为 0，a¹ 的值不累乘到最终结果中。因为要使用 a¹ 推导出 a² 的值，前面 a¹ 的值需要存储，在整个求值过程，可以设置 2 个变量，一个用来存储一路推导出来的值，即aⁱ（i=1，2，4，8），一个用来存储最终结果值。

//存储迭代值
int base =a;
//存储最终结果值
int res=1;
if( 1010 的最后一位是 0 )
	base 的值不能被累乘到 res 中。

第二次迭代，base=base*base，迭代出 a² 的值，因为1010的倒数第 2 位的值为 1。把此次 base 中的值累乘到 res。

//第二次迭代
base *=base;
if( 1010的倒数第二位是 1 )
    把 base 的值累乘到 res 中。
    res*=base

第三次迭代，base=base*base，迭代出 a⁴ 的值，因为 1010的倒数第 3 位的值为 0，此次迭代的值不能累乘到 res 中。

//第三次迭代
base *=base;
if( 1010的倒数第三位是 0 )
    base 中的值不能累乘到 res 中。

第四迭代，base=base*base，迭代出 a⁸ 的值，因为1010的倒数第 1 位的值为 1。把此次 base 中的值累乘到 res。

//第四次迭代
base *=base;
if( 1010的倒数第四位是 1 )
    base 值需要累乘到 res 中。
     res*=base

四次后，整个求解过程结束。从上面的分析可知：

指数转化成二进制后，二进制有多少位，需要迭代多少次。
每次迭代都会得到一个中间值（存储在 base中），至于此值需不需要累乘到最终结果中，则需要根据二进制中的 0和1决定。如果是 0则不需要，1则需要。

有了基本的流程思路就可提供具体的操作。

一种方案是把指数转换的二进制以字符串类型存储。

#include <iostream>
#include <stack>
using namespace std;

/*
* 将数字转换成二进制字符串
*/
string binary(int num) {
	string s="";
	while( num>0 ) {
		s+=num % 2+'0';
		num=num/2;
	}
	return s;
}
/*
*快速幂
*/
int ksm(int a,int n) {
	string s= binary(n);
    //字符串二进制的长度
	int len=s.length();
    //初始化推导数
	int base=a;
    //结果
	int res=1;
	if(s[0]=='1')
        //如果最后一位是 1 ，则初始化为推导数
		res*=base;
	for(int i=1; i<len; i++) {
		base*=base;
		if(s[i]=='1')res*=base;
	}
	return res;
}

int main(int argc, char** argv) {
	int a,n;
	cin>>a>>n;
	int res= ksm(a,n);
	cout<<res;
	return 0;
}

上述算法方案虽然可行，但是，很不优雅。快速幂的本质是累乘，其解决过程并不难，但是，算法中会有一个分支，就是需要根据二进制某位的值是 0 还是 1 决定是否累乘到结果中，所以，解决本题目的关键就是在每一次迭代过程中如何检查二进制的某位的值是0还是1。

凡是涉及到二进制操作时，第一想法便是使用位运算符。此题使用 &（与运算）和>>(右移运算)便可解决。其流程如下：

每次迭代时，把n=1010和1相与(n&1)，可判断最后一位是是 1还是 0。位运算法则，1 和 1相与为1，0和1相与为0。
当前迭代结束时，把n=1010向右移一位(n>>1)，则 n=101。为下一次迭代做准备。
重复上述两步，直到 n=0。

//使用位运算符实现快速幂
int ksm(int a,int n) {
	int base=a;
	int res=1;
	while(n>0) {
		if(n & 1==1 ) {
			//如果 n　最后一位是 1
			res*=base;
		}
		base*=base;
		//右移
		n=n>>1;
	}
	return res;
}

第二种方案的代码量明显少于第一种方案，且没有改变数据本身的类型。时间复杂度都是O(logn)。

3. 前缀和

给定一个长度为 N 的数列 A ，然后进行若干次查询 , 每一次给定一个整数 T , 求出最大的 k , 满足 A[1]+A[2]……A[K]<=T。

第一种解题方案，先对数列进行前缀和预处理，然后使用二分查找算法。

对原数列预处理，求出前缀和。

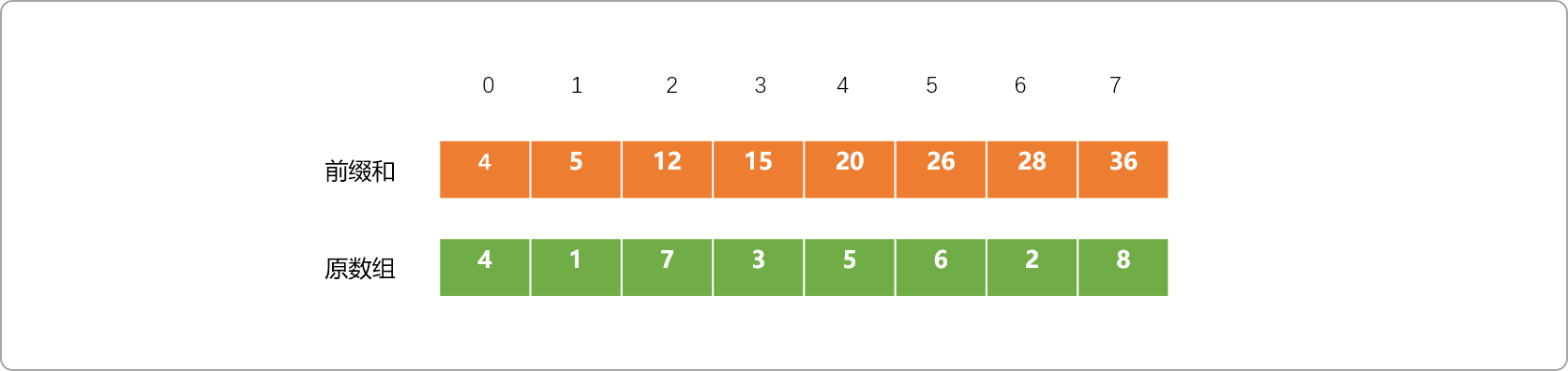
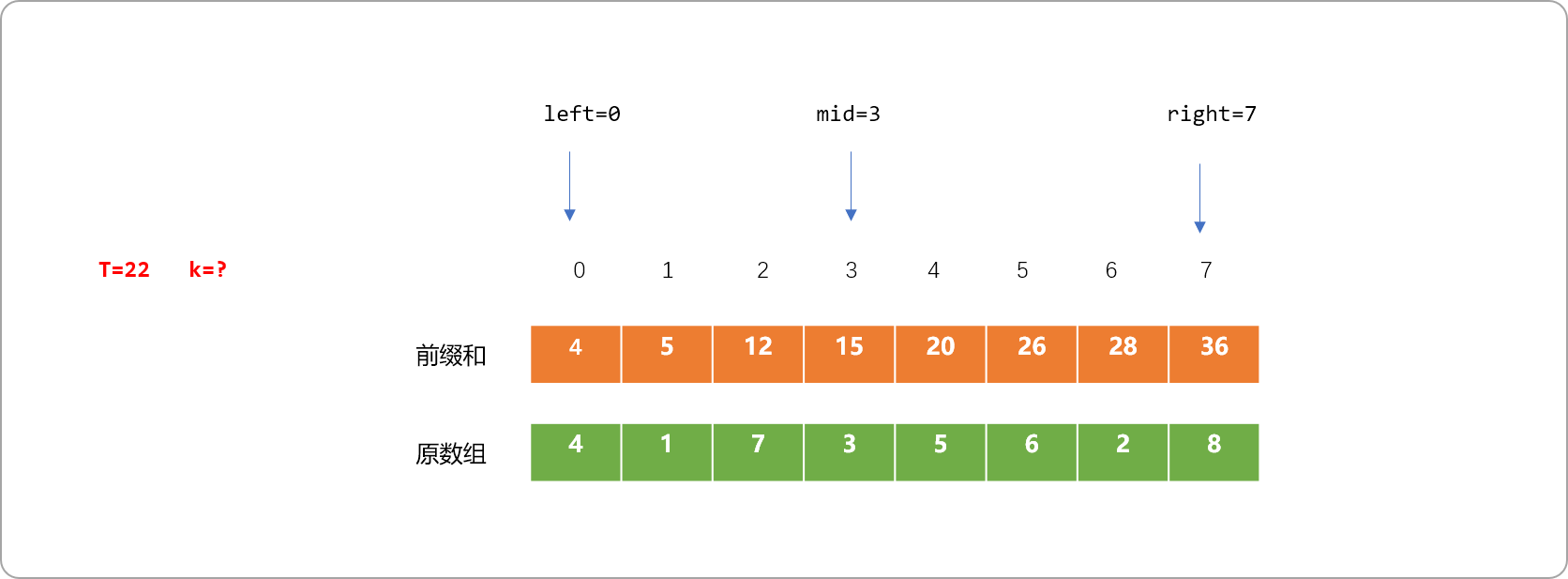
如输入 T=22，求 k。可使用二查找算法。

编码实现：

#include <iostream>
#include <stack>
using namespace std;
int main() {
	//原数组
	int nums[8]= {4,1,7,3,5,6,2,8};
	//前缀和数组
	int sum[8]= {0};
	for(int i=0; i<8; i++) {
		if(i==0)sum[i]=nums[i];
		else sum[i]=sum[i-1]+nums[i];
	}
	int t,k;
	cin>>t;
	int left=0,right=7;
	int midPos,midVal;
	//二分查找
	while(left<=right) {
		midPos=(right+left)>>1;
		midVal=sum[midPos];
		if( midVal<=t )left=midPos+1;
		else right=midPos-1;
	}
	k=right;
	cout<<"最大的位置:"<<k<<endl;;
	return 0;
}

二分查找的时间复杂度为O(logn)。

也可以使用倍增算法实现查找K的过程。

#include<iostream>
using namespace std;
int main() {
	//原数组
	int nums[8]= {4,1,7,3,5,6,2,8};
	//前缀和数组
	int sum[8]= {0};
	for(int i=0; i<8; i++) {
		if(i==0)sum[i]=nums[i];
		else sum[i]=sum[i-1]+nums[i];
	}
	int k=0,i=1,s=0,t;
	cin>>t;
	while(i!=0) {
		if(s+sum[k+i]-sum[k]<=t && sum[k+i]-sum[k]>0) {
			s+=sum[k+i]-sum[k];
			k+=i;
			i<<=1;
		} else i>>=1;
	}
	printf("%lld\n",k);
	return 0;
}