1. 前言
图的常用存储方式有 2 种:
-
邻接炬阵。
-
链接表。
邻接炬阵的优点和缺点都很明显。优点是简单、易理解,但是对于大部分图结构而言,都是稀疏的,使用矩阵存储,空间浪费就较大。
链接表相比较邻接矩阵存储方案,使用起来更方便,对于空间的使用是刚好够用原则,不会产生太多空间浪费。理解起来可能会有点难度。
本文将以链接表方式存储图结构,在此基础上实现无向无权图最短路径搜索。
2. 链接表
2.1 存储思路
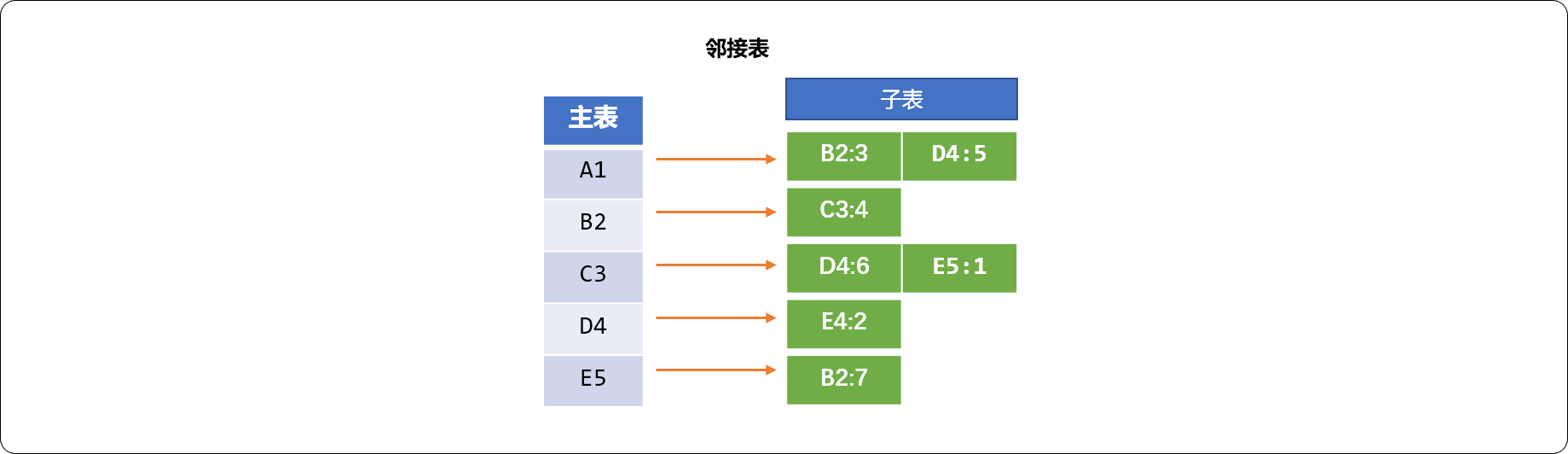
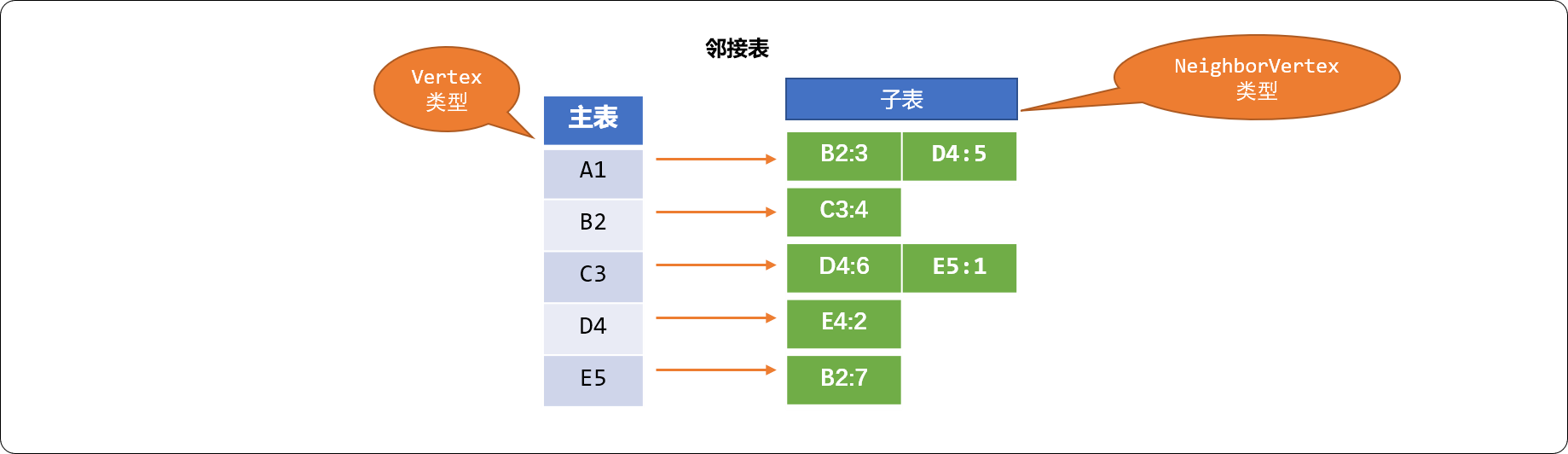
使用链接表实现图的存储时,有主表和子表概念。
- 主表: 用来存储图对象中的所有顶点数据。
- 子表: 每一个顶点自身会维护一个子表,用来存储与其相邻的所有顶点数据。
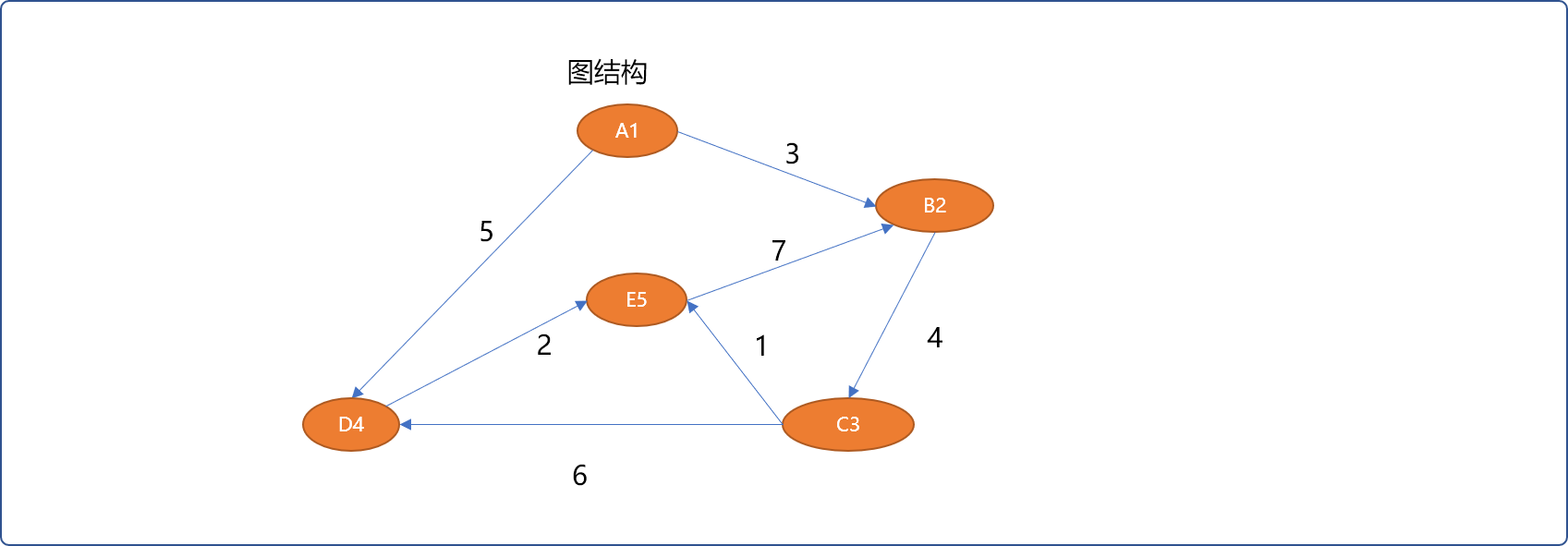
如下图结构中有 5 个顶点,使用链接表保存时,需要主表 1 张,子表 5 张。链接表的优点是能够紧凑地表示稀疏图。
2.2 图的存储实现
2.2.1 项点类
因顶点本身是具有特定的数据含义(如,可能是城市、公交车站、网址、路由器……),需要一个顶点类承载顶点的有效数据。并在顶点类中提供维护自身信息的函数。
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
template<typename T>
struct Vertex {
// 顶点的编号
int vid;
// 顶点有效负荷
T value;
// 是否被访问过:False 没有 True:有
bool visited ;
//相邻顶点类型
template<typename T1>
struct NeighborVertex {
Vertex<T1> *vertex;
//和相邻顶点的权重
int weigth;
//兄弟顶点
NeighborVertex<T1> *next;
NeighborVertex( Vertex<T1> *ver,int weigth) {
this->vertex=ver;
this->weigth=weigth;
this->next=NULL;
}
};
// 相邻顶点链表
NeighborVertex<T> * head;
//搜索时的前驱结点
Vertex* preVertex;
//无参构造
Vertex() {
this->vid=0;
this->visited=false;
this->head=NULL;
}
//有参构造
Vertex(int vid,T value) {
this->vid=vid;
this->visited=false;
this->head=NULL;
this->value=value;
}
/*
*在链表中使用头部插入方案添加邻接顶点
*nbrVer:相邻顶点
*weight:无向无权重图,权重默认设置为 1
*/
void addNeighbor(Vertex<T> *nbrVer,int weigth) {
NeighborVertex<T> * newNbrVer=new NeighborVertex<T>(nbrVer,weigth);
//头部添加
if(this->head==NULL) {
this ->head=newNbrVer;
} else {
newNbrVer->next=this->head;
this->head=newNbrVer;
}
}
/*
* 显示与当前顶点相邻的顶点
*/
vector<Vertex<T> *> showAllNeighbor() {
NeighborVertex<T> *move=this->head;
vector<Vertex<T> *> allNeighbor;
while(move!=NULL) {
allNeighbor.push_back(move->vertex);
move->vertex->desc();
cout<<"_权重"<<move->weigth<<"\t";
move=move->next;
}
return allNeighbor;
}
/*
*判断与某顶点是否相邻,并返回权重 0 表示与此顶点不相邻
*/
int isNeighbor(NeighborVertex<T> *ver) {
NeighborVertex<T> *move=this->head;
while(move!=NULL && move->vertex->value!=ver->value) {
move=move->next;
}
if (move==NULL)
return 0;
else
return move->weigth;
}
//顶点的自我显示
void desc() {
cout<<"顶点["<<this->vid<<"_"<<this->value<<"]";
}
};
顶点类结构需要说明地方:
visited:用于搜索路径算法中,检查节点是否已经被搜索过。head:存储与顶点相邻的顶点信息,也称为相邻顶点,相邻顶点需要包括2方面信息,一是顶点Vertex信息,二是权重。这里提供了NeighborVertex类型,在Vertex类型的基础之上封装了权重。
2.2.2 图类
图类用于维护l图中的所有顶点以及顶点之间的关系,以及针对于图的相关算法。
template<typename T>
class Graph {
private:
// 一维数组,存储节点
Vertex<T>** vertexs;
// 顶点编号,从 0 开始
int vnums;
//一维数组大小
int size;
public:
Graph(int size) {
//初始一给数组大小
this->vertexs=new Vertex<T>*[size];
this->vnums=0;
this->size=size;
}
//添加新顶点
Vertex<T> * addVertex(T value);
//为顶点添加相邻顶点
void addNeighbor(T parentValue,T nbrValue,int weight);
//按值查找顶点
Vertex<T> * findVertexByValue(T value);
//按编号查找顶点
Vertex<T> * findVertexById(int id);
//显示所有顶点
void showAllVers();
};
查找函数:
查找算法有 2 种方案:
- 按值查找。
/*
*按值查找顶点是否存在
*/
template<typename T>
Vertex<T> * Graph<T>::findVertexByValue(T value) {
for(int i=0; i<Graph<T>::vnums; i++) {
if(Graph<T>::vertexs[i]==NULL)
continue;
if(Graph<T>::vertexs[i]->value==value) {
return Graph<T>::vertexs[i];
}
}
return NULL;
}
- 按编号查找。
/*
*按编号查找顶点是否存在
*/
template<typename T>
Vertex<T> * Graph<T>::findVertexById(int id) {
for(int i=0; i<Graph<T>::vnums; i++) {
if(Graph::vertexs[i]->vid==id) {
return Graph<T>::vertexs[i];
}
}
return NULL;
}
添加新顶点函数: 先查找是否存在顶点,没有就添加。
顶点的编号由图对象内部指定,便于统一管理。
/*
*添加新的顶点
*/
template<typename T>
Vertex<T> * Graph<T>::addVertex(T value) {
//检查此顶点是否存在
Vertex<T> * ver= Graph<T>::findVertexByValue(value);
if(ver==NULL) {
//创建新的顶点
ver=new Vertex<T>(Graph<T>::vnums,value);
Graph::vertexs[Graph<T>::vnums]=ver;
Graph<T>::vnums++;
}
return ver;
}
添加顶点之间的关系:
//为顶点添加相邻顶点
template<typename T>
void Graph<T>::addNeighbor(T parentValue,T nbrValue,int weight) {
Vertex<T> * parentVer= Graph<T>::findVertexByValue(parentValue);
if(parentVer==NULL)
parentVer=Graph<T>::addVertex(parentValue);
Vertex<T> * nbrVer= Graph<T>::findVertexByValue(nbrValue);
if(nbrVer==NULL)
nbrVer=Graph<T>::addVertex(nbrValue);
//调用顶点的函数
parentVer->addNeighbor(nbrVer,weight);
}
显示所有顶点:
template<typename T>
void Graph<T>::showAllVers() {
for(int i=0; i<Graph<T>::vnums; i++) {
Graph::vertexs[i]->desc();
cout<<endl<<"\t相邻顶点:";
//输出相邻顶点
Graph::vertexs[i]->showAllNeighbor();
cout<<endl;
}
}
测试图中的函数:
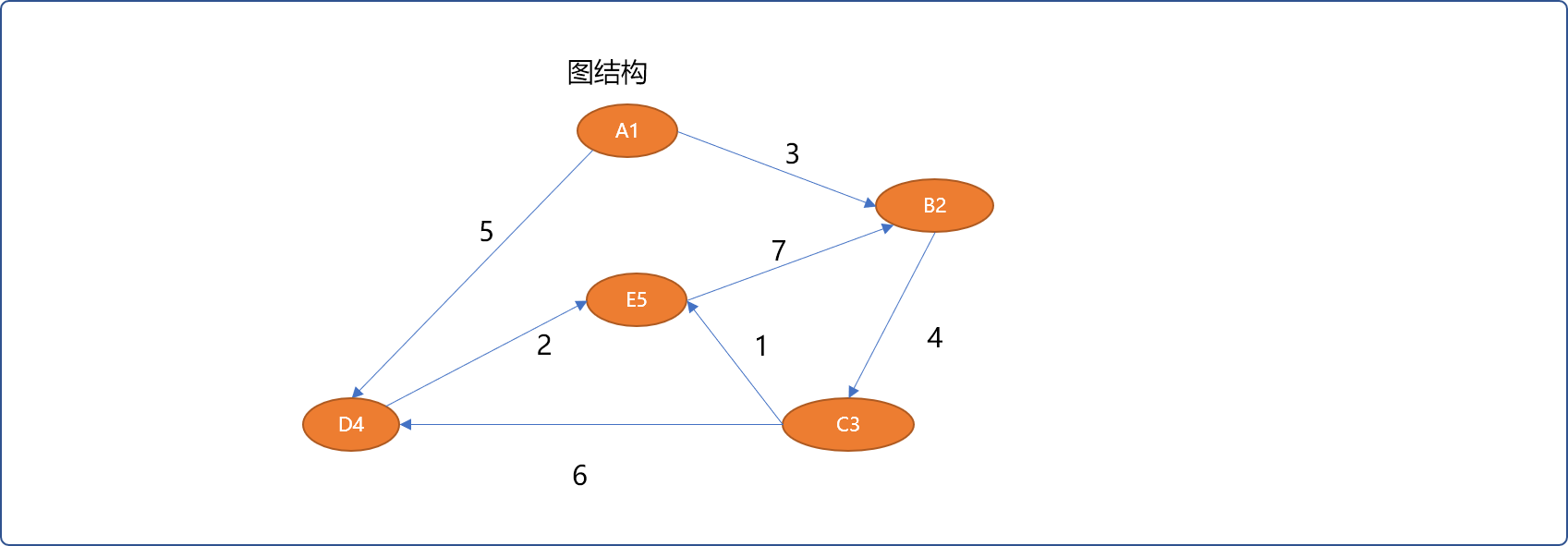
存储如下图结构中顶点以及顶点之间的信息:
int main(int argc, char** argv) {
//实例化图
Graph<char> *graph=new Graph<char>(10);
//添加几个顶点 A,B C D E
char vers[5]= {'A','B','C','D','E'};
for(int i=0; i<5; i++) {
graph->addVertex(vers[i]);
}
//添加顶点之间的关系(A -(3)-》B )
graph->addNeighbor('A','B',3);
//添加顶点之间的关系(A -(5)-》D )
graph->addNeighbor('A','D',5);
//添加顶点之间的关系(B -(4)-》c )
graph->addNeighbor('B','C',4);
//添加顶点之间的关系(C -(6)-》D)
graph->addNeighbor('C','D',6);
//添加顶点之间的关系(C -(1)-》E)
graph->addNeighbor('C','E',1);
//添加顶点之间的关系(D -(2)-》E)
graph->addNeighbor('D','E',2);
//添加顶点之间的关系(E -(7)-》B)
graph->addNeighbor('E','B',7);
//输出所的顶点
graph->showAllVers();
return 0;
}
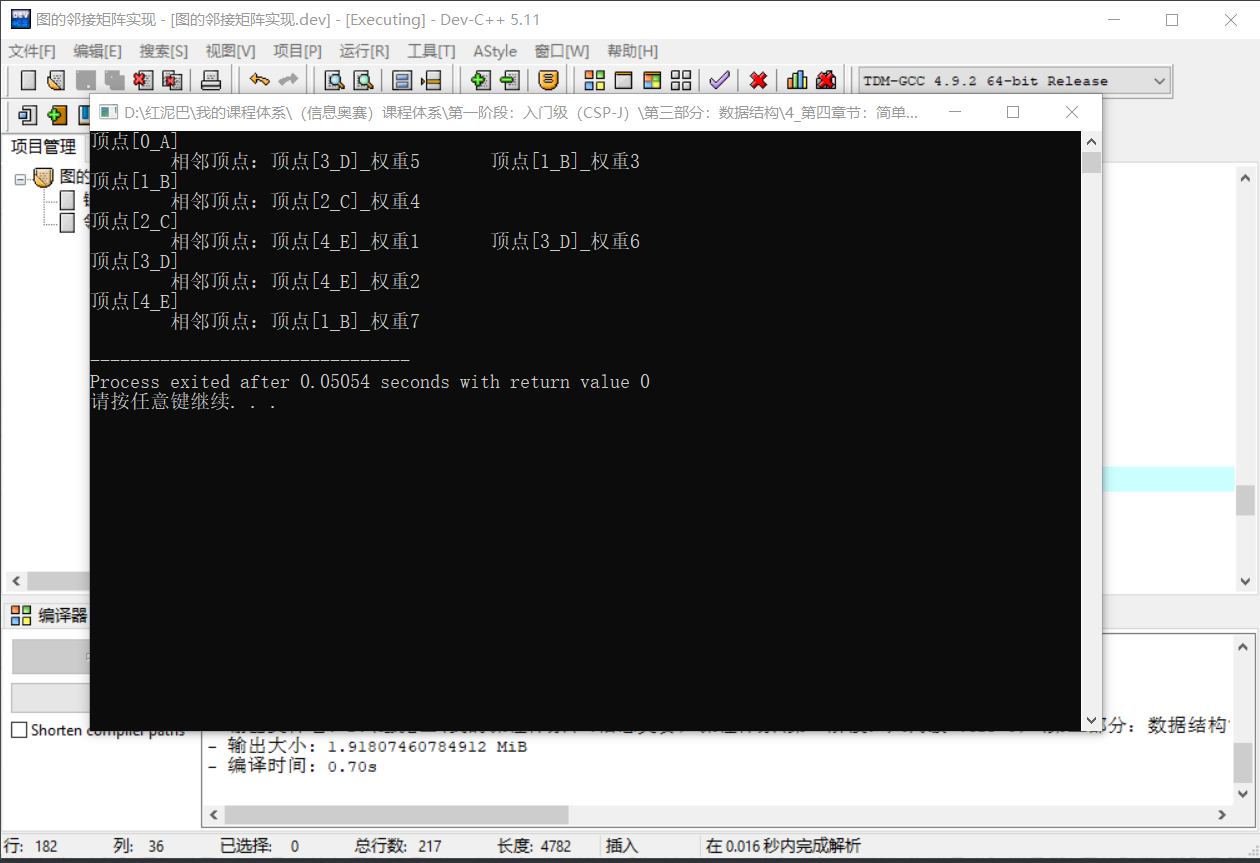
输出结果:
3. 最短路径算法
从图结构可知,从一个顶点到达另一个顶点,不止一条可行路径,在众多路径我们总是试图选择一条最短路径。当然,需求不同,衡量一个路径是不是最短路径的标准也会不同。
如打开导航系统后,最短路径可能是费用最少的那条、可能是速度最快的那条、也可能是量程数最少的或者是红绿灯最少的……
在无权无向图中,以经过的边数最少的路径为最短路径。在无权无向图中找到最短路径相对简单。
在有向加权图中,会以附加在每条边上的权重的数据含义来衡量。权重可以是时间、速度、量程数……
3.1 算法思路
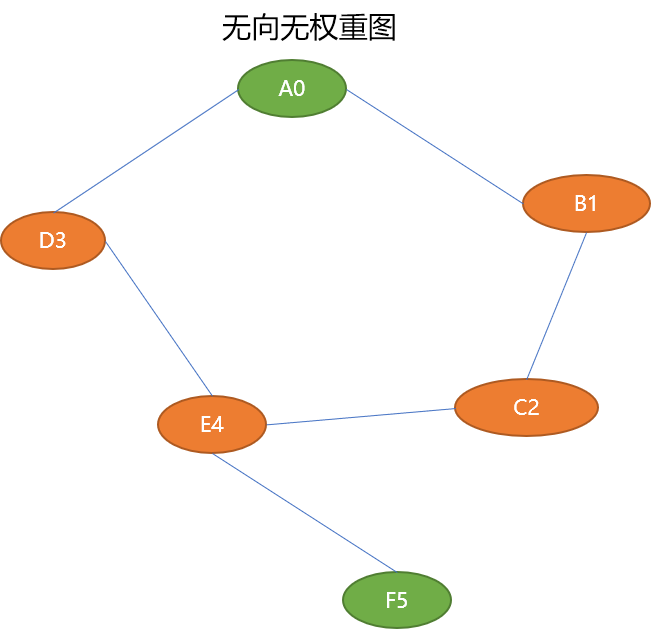
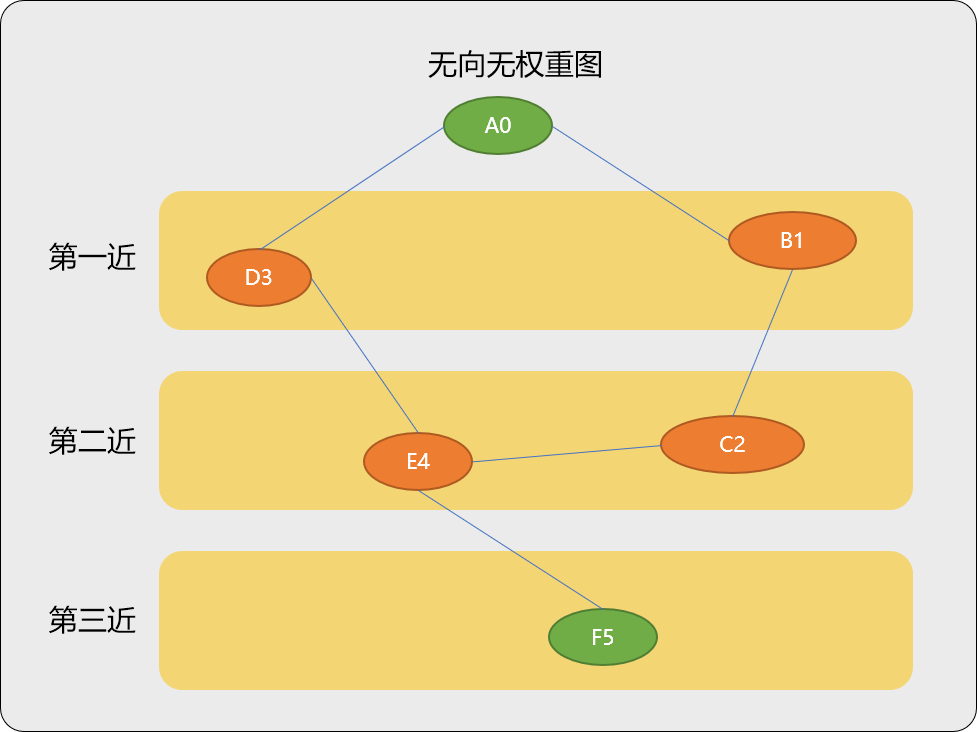
查找无向图中任意两个顶点间的最短路径长度,可以直接使用广度搜索算法。如下图求解 A0 ~ F5 的最短路径。
Tips: 无向图中任意
2个顶点间的最短路径长度由边数决定。
广度优先搜索算法流程:
广度优先搜索算法的基本原则:以某一顶点为参考点,先搜索离此顶点最近的顶点,再搜索离最近顶点的最近顶点……以此类推,一层一层向目标顶点推进。
如从顶点 A0 找到顶点 F5。先从离 A0 最近的顶点 B1、D3 找起,如果没找到,再找离 B1、D3 最近的顶点 C2、E4,如果还是没有找到,再找离 C2、E4 最近的顶点 F5。
Tips: 因为每一次搜索都是采用最近原则,最后搜索到的目标也一定是最近的路径。
也因为采用最近原则,在搜索过程中所经历到的每一个顶点的路径都是最短路径。
最近+最近,结果必然还是最近。
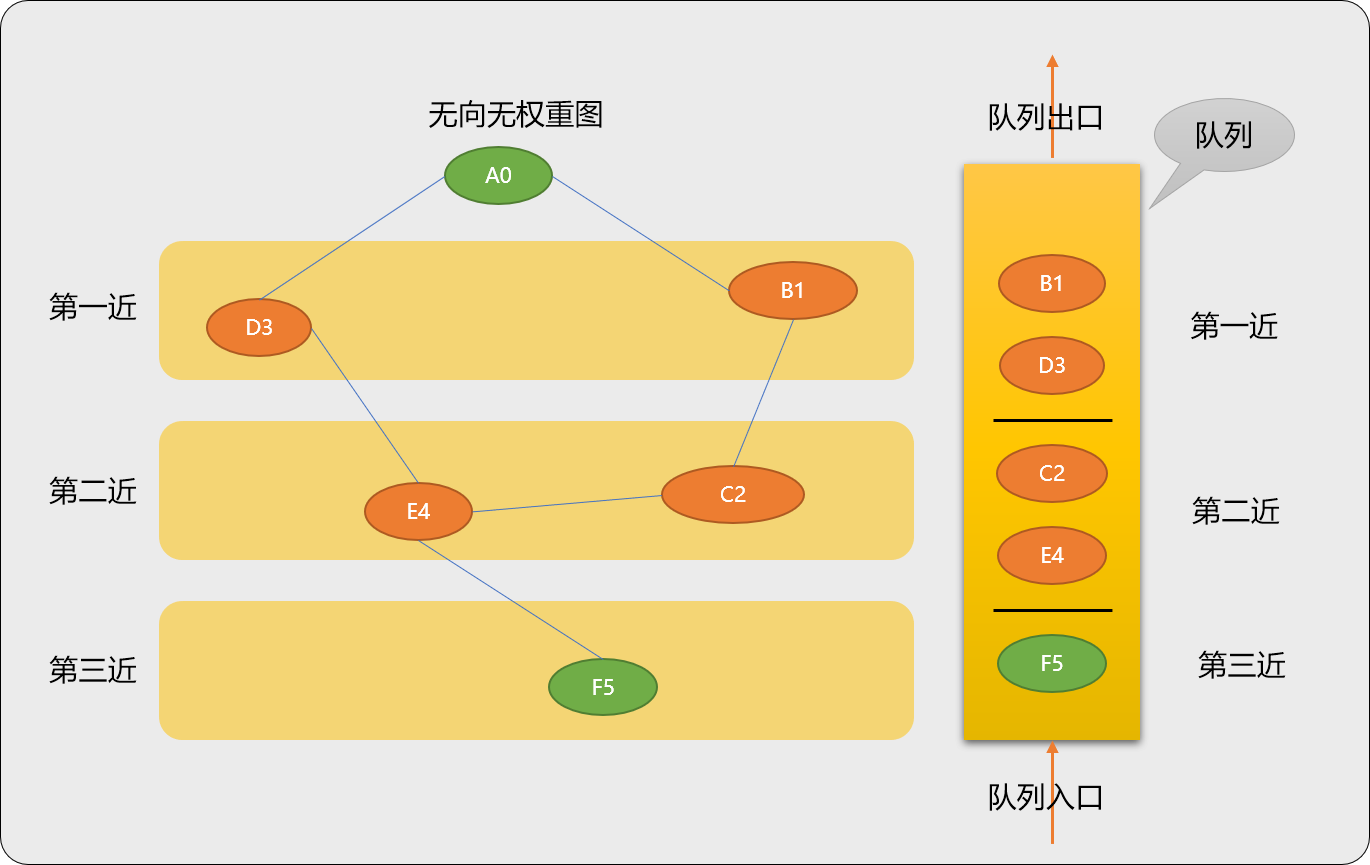
显然,广度优先搜索的最近搜索原则是符合先进先出思想的,具体算法实施时可以借助队列实现整个过程。
算法流程:
-
先确定起始点
A0。 -
找到
A0的2个后序顶点B1、D3(或者说B1、D3的前序顶点是A0),压入队列中。除去起点A0,B1、D3顶点属于第一近压入队列的节点。B1和D3压入队列的顺序并不影响A0~B1或A0~D3的路径距离(都是 1)。A0~B1的最短路径长度为 1。A0~D3的最短路径长度为 1。 -
从队列中搜索
B1时,找到B1的后序顶点C2并压入队列。B1是C2的前序顶点。B1~C2的最短路径长度为 1,而又因为A0~B1的最短路径长度为 1 ,所以A0~C2的最短路径为 2 -
B1搜索完毕后,在队列中搜索B3时,找到B3的后序顶点E4,压入队列。因B1和D3属于第一近顶点,所以这2个顶点的后序顶点C2、E4属于第二近压入队列,或说A0-B1-C2、A0-D3-E4的路径距离是相同的(都为 2)。 -
当搜索到
C2时,此时队列没有压入操作。 -
当 搜索到
E4时,E4有2个相邻顶点C2、F5,因C2已经压入过,所以仅压入F5。因F5是由第二近顶点压入,所以F5是属于第三近压入顶点。A0-D3-E4-F5的路径为 3。
3.2 编码实现
在图类添加广度搜索函数:
在图类添加如下函数:使用广度优先搜索算法查找顶点与顶点之间的路径。
广度优先搜索算法有一个核心点,当搜索到某一个顶点后,需要找到与此顶点相邻的其它顶点,并压入队列中。pushQueue 方法就是做这件事情的。如果某一个顶点曾经进过队列,就不要再重复压入队列了。
template<typename T>
class Graph {
private:
//省略……
//保存所有使用广度算法搜索到的路径
vector<vector<Vertex<T> *> > allPaths;
public:
//省略……
//把某一顶点的相邻顶点压入队列
void pushQueue(queue<Vertex<T> *> & myQueue,Vertex<T> * vertex);
//广度搜索路径
void bfsNearestPath(T from,T to);
//输出广度搜索到的所有路径
void showAllPaths();
};
pushQueue的函数实现:
//把某一顶点的相邻顶点压入队列
template<typename T>
void Graph<T>::pushQueue(queue<Vertex<T> *> & myQueue,Vertex<T> * vertex) {
//查找 vertex 的相邻顶点
cout<<vertex->value<<"相邻顶点:"<<endl;
vector<Vertex<T> *> allVers=vertex->showAllNeighbor();
for(int i=0; i<allVers.size(); i++) {
if(allVers[i]->visited==false) {
//设置前驱顶点
allVers[i]->preVertex=vertex;
//压入队列中
myQueue.push(allVers[i]);
//设置为已经压入
allVers[i]->visited=true;
}
}
cout<<endl;
}
bfsNearestPath广度搜索算法实现:
//广度搜索路径
template<typename T>
void Graph<T>::bfsNearestPath(T from,T to) {
//队列:广度搜索要使用队列
queue<Vertex<T> *> myQueue;
//临时路径
vector<Vertex<T> *> tmpPath;
//检查顶点是否存在
Vertex<T> * fromVer= Graph<T>::findVertexByValue(from);
Vertex<T> * toVer= Graph<T>::findVertexByValue(to);
if(fromVer==NULL || toVer==NULL)
return;
tmpPath.push_back(fromVer);
//把 fromVer 顶点的相邻顶点压入队列中,fromVer 本身可以不用压入
Graph<T>::pushQueue(myQueue,fromVer);
while(!myQueue.empty()) {
//出队列
Vertex<T> * ver= myQueue.front();
myQueue.pop();
if(ver->preVertex==fromVer) {
//如果前驱是 fromVer
tmpPath.push_back(ver);
//添加新路径
Graph<T>::allPaths.push_back(tmpPath);
//把临时路径的最后一个顶点删除
tmpPath.pop_back();
} else {
//扫描所有路径
for(int i=0; i<Graph<T>::allPaths.size(); i++) {
tmpPath = Graph<T>::allPaths[i];
//得到路径中的最后一个顶点
Vertex<T> * tmpVer =tmpPath.back();
if (ver->preVertex==tmpVer) {
tmpPath.push_back(ver);
//allPaths[i]=tmpPath;
Graph<T>::allPaths.push_back(tmpPath);
}
}
}
if(ver->value==toVer->value) {
break;
} else {
Graph<T>::pushQueue(myQueue,ver);
}
}
}
显示顶点之间的路径信息:
/*
*显示搜索到的路径
*/
template<typename T>
void Graph<T>::showAllPaths() {
for(int i=0; i<Graph<T>::allPaths.size(); i++) {
vector<Vertex<T> *> vec=Graph<T>::allPaths[i];
int pathWeight=0;
for(int j=0; j<vec.size(); j++) {
pathWeight++;
vec[j]->desc();
cout<<"-";
}
cout<<"路径长度:"<<pathWeight-1<<endl;
}
}
测试代码: 因为测试的是无向无权重图,顶点之间的权重默认为 1。
nt main(int argc, char** argv) {
//实例化图
Graph<char> *graph=new Graph<char>(10);
//添加几个顶点 A,B C D E
char vers[6]= {'A','B','C','D','E','F'};
for(int i=0; i<6; i++) {
graph->addVertex(vers[i]);
}
//添加顶点之间的关系(A -(3)-》B )
graph->addNeighbor('A','B',1);
//添加顶点之间的关系(A -(5)-》D )
graph->addNeighbor('A','D',1);
//添加顶点之间的关系(B -(4)-》c )
graph->addNeighbor('B','C',1);
//添加顶点之间的关系(C -(6)-》D)
graph->addNeighbor('D','E',1);
//添加顶点之间的关系(C -(1)-》E)
graph->addNeighbor('C','E',1);
//添加顶点之间的关系(D -(2)-》E)
graph->addNeighbor('E','F',1);
//输出所的顶点
graph->showAllVers();
//广度搜索A 到 F 的路径,中间会经过其它顶点
graph->bfsNearestPath('A','F');
cout<<"\n路径信息:"<<endl;
graph->showAllPaths();
return 0;
}
输出结果:
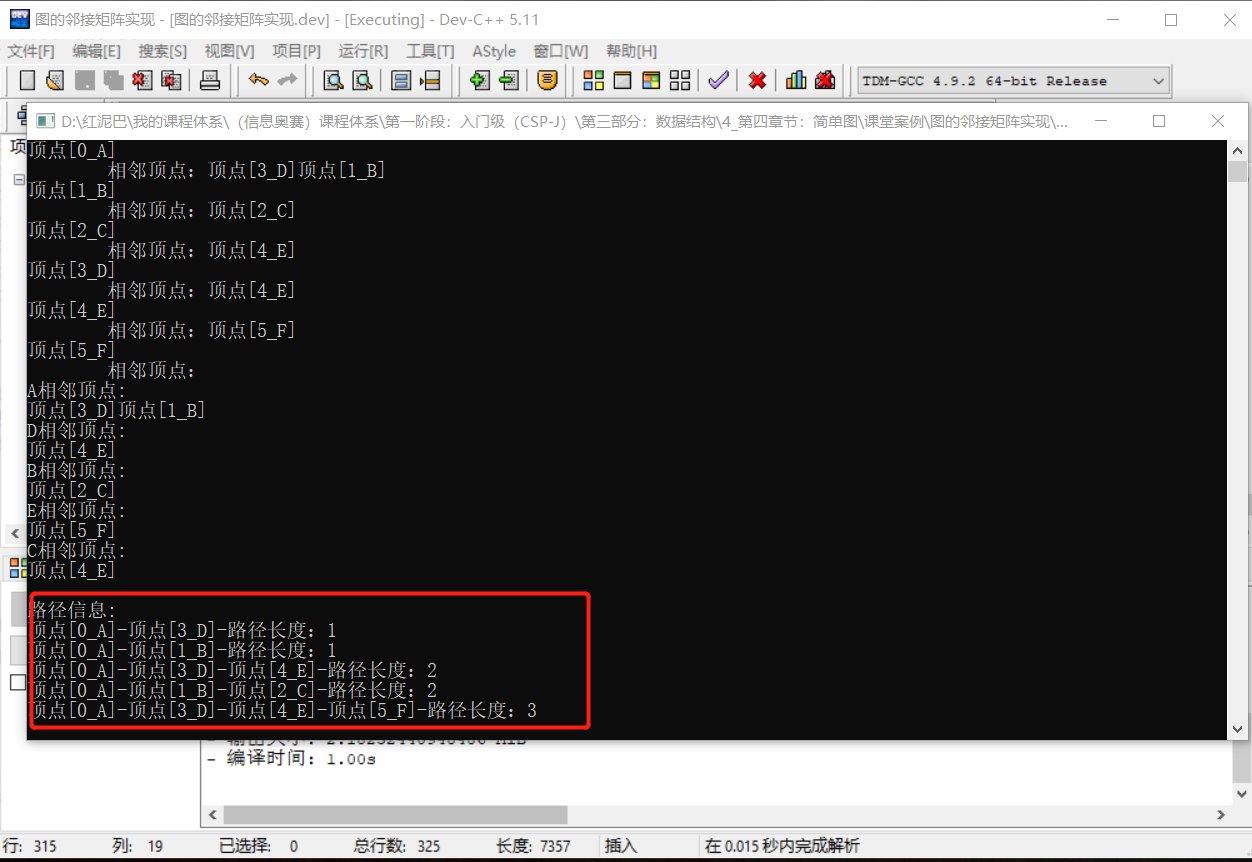
无向无权重图中,查找起始点到目标点的最短路径,使用广度优先搜索算法便可实现。
但如果是有向加权图,可能不会称心如愿。因有向加权图中的边是有权重的。故对于有向加权图则需要另择方案。
4. 总结
本文讲解了如何使用链表存储图,以及使用广度搜索算法实现无向无权重图中顶点之间的路径搜索。