机器学习技术（八）——朴素贝叶斯算法实操

一、引言

上文讲述了逻辑回归在分类任务上的应用及算法原理：https://blog.csdn.net/tianhai12/article/details/132632208

本文着重实践，采用贝叶斯方法对大样本犯罪信息进行训练，得出关于特征的预测方法并与逻辑回归模型进行多维度的比较。关于算法原理参考西瓜书150-154页

二、导入相关依赖库

#导入相关依赖库
import pandas as pd
import numpy as np
import pandas as pd
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import log_loss
from sklearn.naive_bayes import BernoulliNB
from sklearn.linear_model import LogisticRegression
import time

import warnings
warnings.filterwarnings('ignore')

三、读取并查看数据

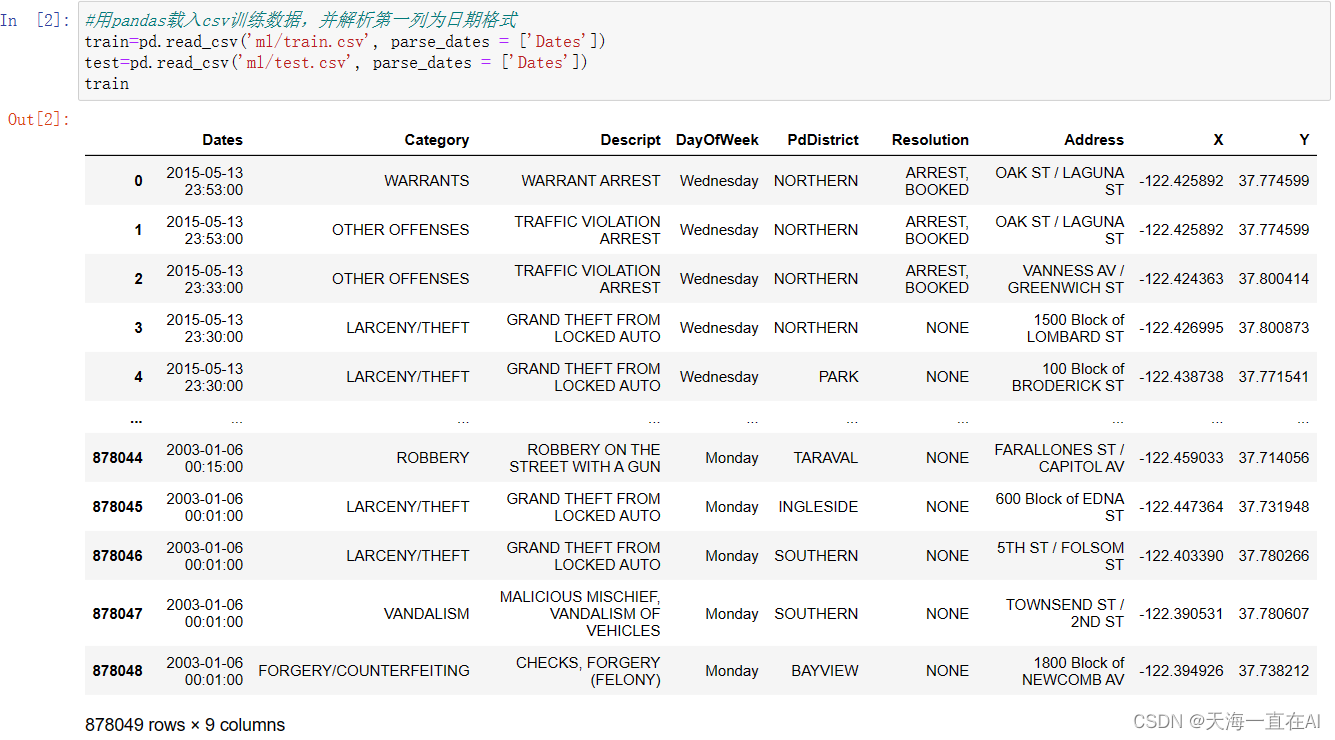
将大样本犯罪数据读入，其中样本被分为训练集以及测试集。

数据集：https://download.csdn.net/download/tianhai12/88275733

输入：

#用pandas载入csv训练数据，并解析第一列为日期格式
train=pd.read_csv('ml/train.csv', parse_dates = ['Dates'])
test=pd.read_csv('ml/test.csv', parse_dates = ['Dates'])
train

部分训练集数据显示如下，每位用户共有9组特征。

四、数据预处理

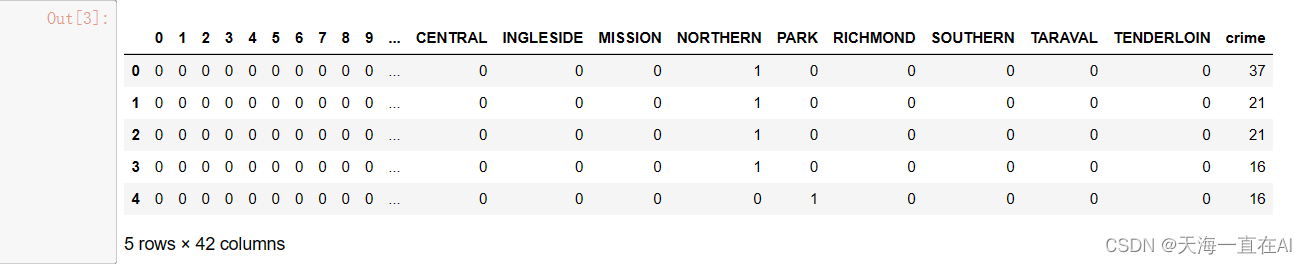
我们将样本中犯罪类型进行编号，并选择其中的Dayofweek（星期几），PdDistrict(地区)以及Dates中的小时作为犯罪罪刑的预测的影响因素，建立新的数据集。

#用LabelEncoder对不同的犯罪类型编号
leCrime = preprocessing.LabelEncoder()
crime = leCrime.fit_transform(train.Category)

#因子化星期几，街区，小时等特征
days = pd.get_dummies(train.DayOfWeek)
district = pd.get_dummies(train.PdDistrict)
hour = train.Dates.dt.hour
hour = pd.get_dummies(hour) 

#组合特征
trainData = pd.concat([hour, days, district], axis=1)
trainData['crime']=crime

#对于测试数据做相同的处理
days = pd.get_dummies(test.DayOfWeek)
district = pd.get_dummies(test.PdDistrict)

hour = test.Dates.dt.hour
hour = pd.get_dummies(hour) 

testData = pd.concat([hour, days, district], axis=1)
trainData.head()

编码完成的数据前五个样本如下所示。

五、构建两种模型进行比较

1、只考虑Dayofweek以及District

首先我们先只考虑Dayofweek以及District两组特征，将数据集按照训练集以及测试集3:2的比例划分，在训练集上建立朴素贝叶斯模型，计算建模所需时间并输出，并在测试集上进行预测输出损失函数的log值；再在训练集上建立逻辑回归模型，计算建模所需时间并输出，并在测试集上进行预测输出损失函数的log值。

#只取星期几和街区作为分类器输入特征
features = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday', 'BAYVIEW', 'CENTRAL', 'INGLESIDE', 'MISSION',
 'NORTHERN', 'PARK', 'RICHMOND', 'SOUTHERN', 'TARAVAL', 'TENDERLOIN']

#分割训练集(3/5)和测试集(2/5)
training, validation = train_test_split(trainData, train_size=.60)

#朴素贝叶斯建模，计算log_loss
model = BernoulliNB()
nbStart = time.time()
model.fit(training[features], training['crime'])
nbCostTime = time.time() - nbStart
predicted = np.array(model.predict_proba(validation[features]))
print ("朴素贝叶斯建模耗时 %f 秒" %(nbCostTime))
print ("朴素贝叶斯log损失为 %f" %(log_loss(validation['crime'], predicted)))

#逻辑回归建模，计算log_loss
model = LogisticRegression(C=.01)
lrStart= time.time()
model.fit(training[features], training['crime'])
lrCostTime = time.time() - lrStart
predicted = np.array(model.predict_proba(validation[features]))
log_loss(validation['crime'], predicted)


print ("逻辑回归建模耗时 %f 秒" %(lrCostTime))
print ("逻辑回归log损失为 %f" %(log_loss(validation['crime'], predicted)))

输出结果如下，发现两个模型在测试集上损失函数log值差不多，但朴素贝叶斯模型建模消耗时间只需要4.8秒，远小于逻辑回归的107秒。（由于本人电脑有点拉，在你们的电脑可能时间短些，朴素贝叶斯建模甚至能达到0.4秒）

输出：

朴素贝叶斯建模耗时 4.868469 秒
朴素贝叶斯log损失为 2.613760
逻辑回归建模耗时 107.135925 秒
逻辑回归log损失为 2.613217

2、加入犯罪时间节点

将犯罪的时间节点也加入特征，进行二次建模比较两个模型的表现

#添加犯罪的小时时间点作为特征
features = ['Friday', 'Monday', 'Saturday', 'Sunday', 'Thursday', 'Tuesday',
'Wednesday', 'BAYVIEW', 'CENTRAL', 'INGLESIDE', 'MISSION',
'NORTHERN', 'PARK', 'RICHMOND', 'SOUTHERN', 'TARAVAL', 'TENDERLOIN']

hourFea = [x for x in range(0,24)]
features = features + hourFea

#分割训练集(3/5)和测试集(2/5)
training, validation = train_test_split(trainData, train_size=.60)

#朴素贝叶斯建模，计算log_loss
model = BernoulliNB()
nbStart = time.time()
model.fit(training[features], training['crime'])
nbCostTime = time.time() - nbStart
predicted = np.array(model.predict_proba(validation[features]))
print ("朴素贝叶斯建模耗时 %f 秒" %(nbCostTime))
print ("朴素贝叶斯log损失为 %f" %(log_loss(validation['crime'], predicted)))

#逻辑回归建模，计算log_loss
model = LogisticRegression(C=.01)
lrStart= time.time()
model.fit(training[features], training['crime'])
lrCostTime = time.time() - lrStart
predicted = np.array(model.predict_proba(validation[features]))
log_loss(validation['crime'], predicted)
print ("逻辑回归建模耗时 %f 秒" %(lrCostTime))
print ("逻辑回归log损失为 %f" %(log_loss(validation['crime'], predicted)))

利用三组特征进行建模所得与上相似，朴素贝叶斯算法效率更高

输出：

朴素贝叶斯建模耗时 12.705698 秒
朴素贝叶斯log损失为 2.582038
逻辑回归建模耗时 112.633900 秒
逻辑回归log损失为 2.583173

六、总结

通过基于朴素贝叶斯方法探索通过犯罪时间，星期几以及区域来判断犯罪类型，并选择不同特征进行两次建模与逻辑回归方法进行关于建模时间以及在测试集上表现的比较，发现面对相同数据集，朴素贝叶斯方法效率更高