Problem - D - Codeforces

题目大意：有一个长度为n的数组a，每次操作可以选取一个长度为k的所有数互不相同的数组b，令a[bi]=b[i%k+1]，问能否将一个全为零的数组通过任意次操作得到a

1<=k<=n<=1e5

思路：通过上述操作，我们发现k中每两个数可以把一个位置修改成目标值，例如对于题目中给的样例1，我们要将a[1]修改成2，那么k就应该等于[1,2,?]，要将a[2]修改成3，k就等于[2,3,?]，但问号里的数不能与前面的重复也不能超过n，所以可能会覆盖掉之前修改过的数，如果我们从i向a[i]建边，那么存在覆盖就代表着图中存在环。样例1的环如下：

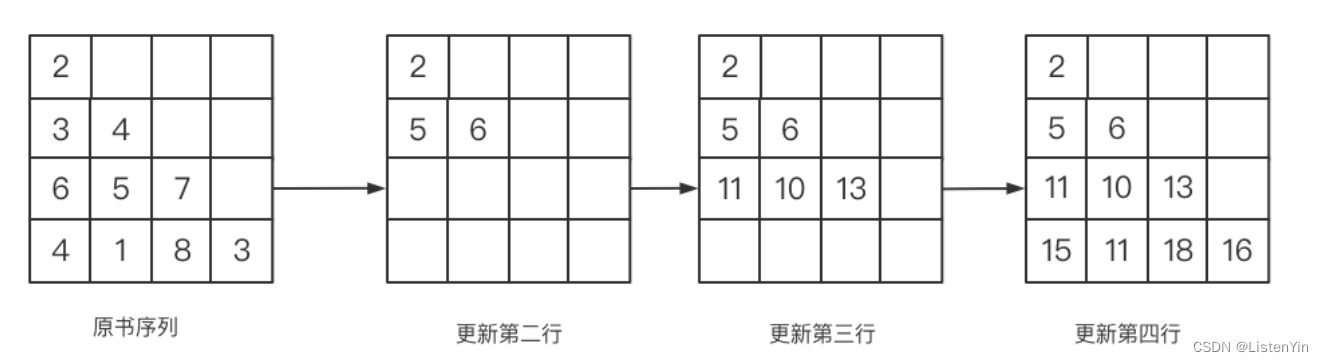
对于单一约束的点，也就是环以外的点，直接按顺序操作即可，对于环内的点，当环的大小大于k时，也就是如下图：

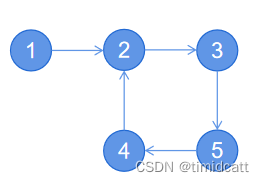
我们先按顺序操作[1,2,3]，[3,5,4]，使位置1,2,3,5上的数都修改完毕，要让位置4上的数也修改好，只能是[4,2,3]，这是会把3修改成4，而我们要的是5，要把3改回去，就要操作[3,5,4]，第4个位置又不行了，所以这样的环永远会出现错误覆盖的情况。

但环的大小小于k时，例如1,2互向指向自己，那k=3时的操作就只能是[1,2,1]，后面填别的数都会错误的覆盖掉其他位置，而这样又与b种数字不能重复矛盾，所以这样的话也没法修改好。

综上，只有所有环的大小等于k时才有合法操作方案，我们首先从入度为0的点开始遍历，先用类似拓扑排序的方法去掉所有环外的点，然后再遍历所有环，检查大小是否为k。

除此之外，还要特判k=1的情况，因为这时只能将第i个位置上的数修改成i，检查a数组即可

#include<bits/stdc++.h>
//#include<__msvc_all_public_headers.hpp>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int n;
bool vis[N];
int to[N];
int in[N];
void init()
{
	for (int i = 1; i <= n; i++)
	{
		in[i] = 0;
		vis[i] = 0;
	}
}
int cnt = 0;
void dfs(int u)
{//遍历环
	vis[u] = 1;
	cnt++;//统计环的大小
	int v = to[u];
	if (!vis[v])
	{
		dfs(v);
	}
}
void solve()
{
	int k;
	cin >> n >> k;
	init();
	if (k == 1)
	{//特判k=1的情况
		bool flag = 1;
		for (int i = 1; i <= n; i++)
		{
			int x;
			cin >> x;
			if (x != i)
				flag = 0;
		}
		cout << (flag ? "Yes" : "No") << endl;
		return;
	}
	for (int i = 1; i <= n; i++)
	{
		int v;
		cin >> v;
		in[v]++;
		to[i] = v;//从i向a[i]建边
	}
	queue<int>q;
	for (int i = 1; i <= n; i++)
	{//放入入度为0的点
		if (!in[i])
		{
			q.push(i);
		}
	}
	while (!q.empty())
	{//用类似拓扑排序的方式标记所有环外的点
		int u = q.front();
		q.pop();
		vis[u] = 1;
		int v = to[u];
		in[v]--;
		if (!in[v])
		{
			q.push(v);
		}
	}
	for (int i = 1; i <= n; i++)
	{//遍历所有环
		if (!vis[i])
		{
			cnt = 0;
			dfs(i);
			if (cnt != k)
			{//检查环的大小是否等于k
				cout << "No" << endl;
				return;
			}
		}
	}
	cout << "Yes" << endl;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}