树型结构和二叉树的概念及特性

news2024/10/6 0:33:07

1. 树型结构

1.1 树的概念

1.2重要专有名词概念

1.3 树的表示形式

1.4 树的应用

编辑

2. 二叉树

2.1 概念

2.2 两种特殊的二叉树

2.3 二叉树的性质

3.有关二叉树性质的练习题

1. 树型结构

1.1 树的概念

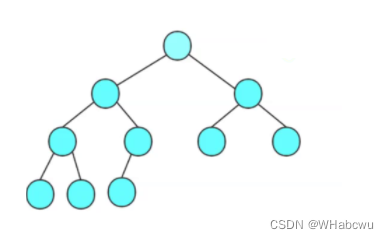
树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

它具有以下的特点：

（1）有一个特殊的结点，称为根结点，根结点没有前驱结点。

（2）除根结点外，其余结点被分成 M(M > 0) 个互不相交的集合 T1 、 T2 、 ...... 、 Tm ，其中每一个集合 Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有 0 个或多个后继。

（3）树是递归定义的。

（4）树形结构中，子树之间不能有交集，否则就不是树形结构。

重要的总结与整理：

1.2重要专有名词概念

重要概念

（1）结点的度 ：一个结点含有子树的个数称为该结点的度；如上图： A 的度为 6

（2）树的度 ：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为 6

（3）叶子结点或终端结点 ：度为 0 的结点称为叶结点；如上图： B 、 C 、 H 、 I... 等节点为叶结点

（4）双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点

（5）孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点

（6）根结点：一棵树中，没有双亲结点的结点；如上图：A

（7）结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推树的高度或深度：树中结点的最大层次；如上图：树的高度为4

以下概念只需了解

（1）非终端结点或分支结点：度不为0的结点；如上图：D、E、F、G...等节点为分支结点

（2）兄弟结点：具有相同父结点的结点互称为兄弟结点；如上图：B、C是兄弟结点

（3）兄弟结点：具有相同父结点的结点互称为兄弟结点；如上图：B、C是兄弟结点

（4）堂兄弟结点 ：双亲在同一层的结点互为堂兄弟；如上图： H 、 I 互为兄弟结点

（5）结点的祖先 ：从根到该结点所经分支上的所有结点；如上图： A 是所有结点的祖先

（6）子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是 A 的子孙

（7）森林：由 m （ m>=0 ）棵互不相交的树组成的集合称为森林

1.3 树的表示形式

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如： 双亲表示法 ， 孩子表示法 、 孩子双亲表示法 、 孩子兄弟表示法 等等。我们这里就简单的了解其中最常用的 孩子兄弟表示法 。

class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}

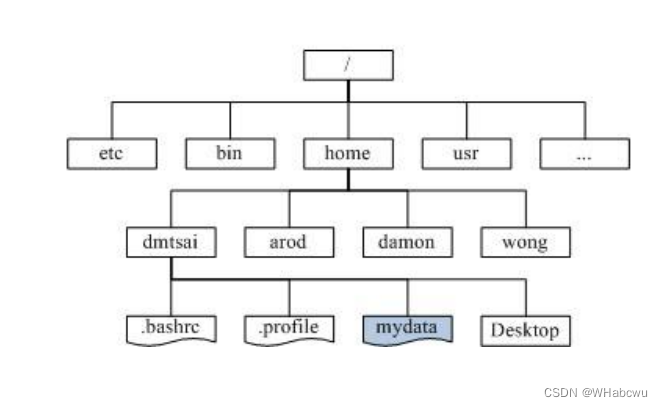
1.4 树的应用

文件系统管理（目录和文件）

2. 二叉树

2.1 概念

一棵二叉树是结点的一个有限集合，该集合：

1. 或者为空

2. 或者是由 一个根节 点加上两棵别称为 左子树 和 右子树 的二叉树组成。

从上图可以看出：

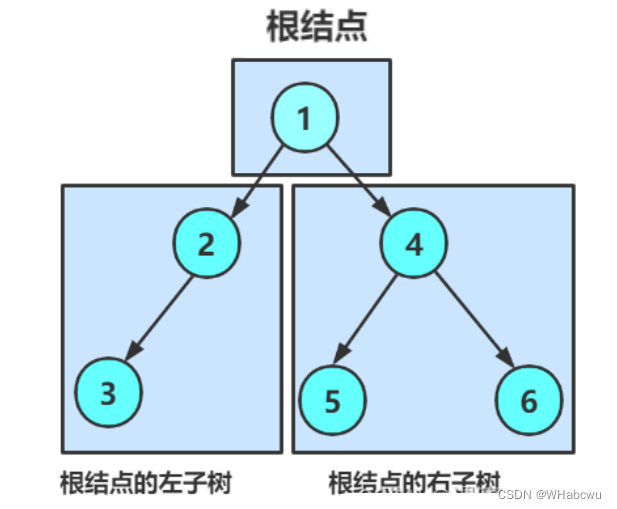
1. 二叉树不存在度大于 2 的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2.2 两种特殊的二叉树

1. 满二叉树 : 一棵二叉树，如果 每层的结点数都达到最大值，则这棵二叉树就是满二叉树 。也就是说，如果一棵二叉树的层数为 K，且结点总数是(2^K)-1 ，则它就是满二叉树 。

2. 完全二叉树 : 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为K 的满二叉树中编号从 0 至 n-1的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

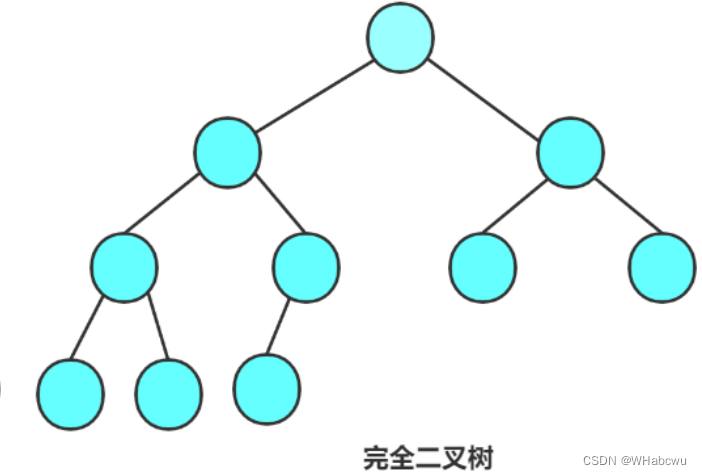
2.3 二叉树的性质

1. 若规定 根结点的层数为 1 ，则一棵 非空二叉树的第 i 层上有（2^i-1) (i>0) 个结点

性质1： 用来求每层有多少个节点

2. 若规定只有 根结点的二叉树的深度为 1 ，则 深度为 K的二叉树的最大结点数是(2^K)-1

(k>=0)

3. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 ＝ n2 ＋ 1

4.具有n个结点的完全二叉树的深度k为：

注意：向上取整

5. 对于具有 n 个结点的完全二叉树 ，如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ，则对于 序号为 i 的结点有 ：

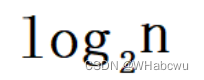
若 i>0 ， 双亲序号： (i-1)/2 ； i=0 ， i 为根结点编号 ，无双亲结点

若 2i+1<n ，左孩子序号： 2i+1 ，否则无左孩子

若 2i+2<n ，右孩子序号： 2i+2 ，否则无右孩子