用javascript分类刷leetcode23.并查集(图文视频讲解)

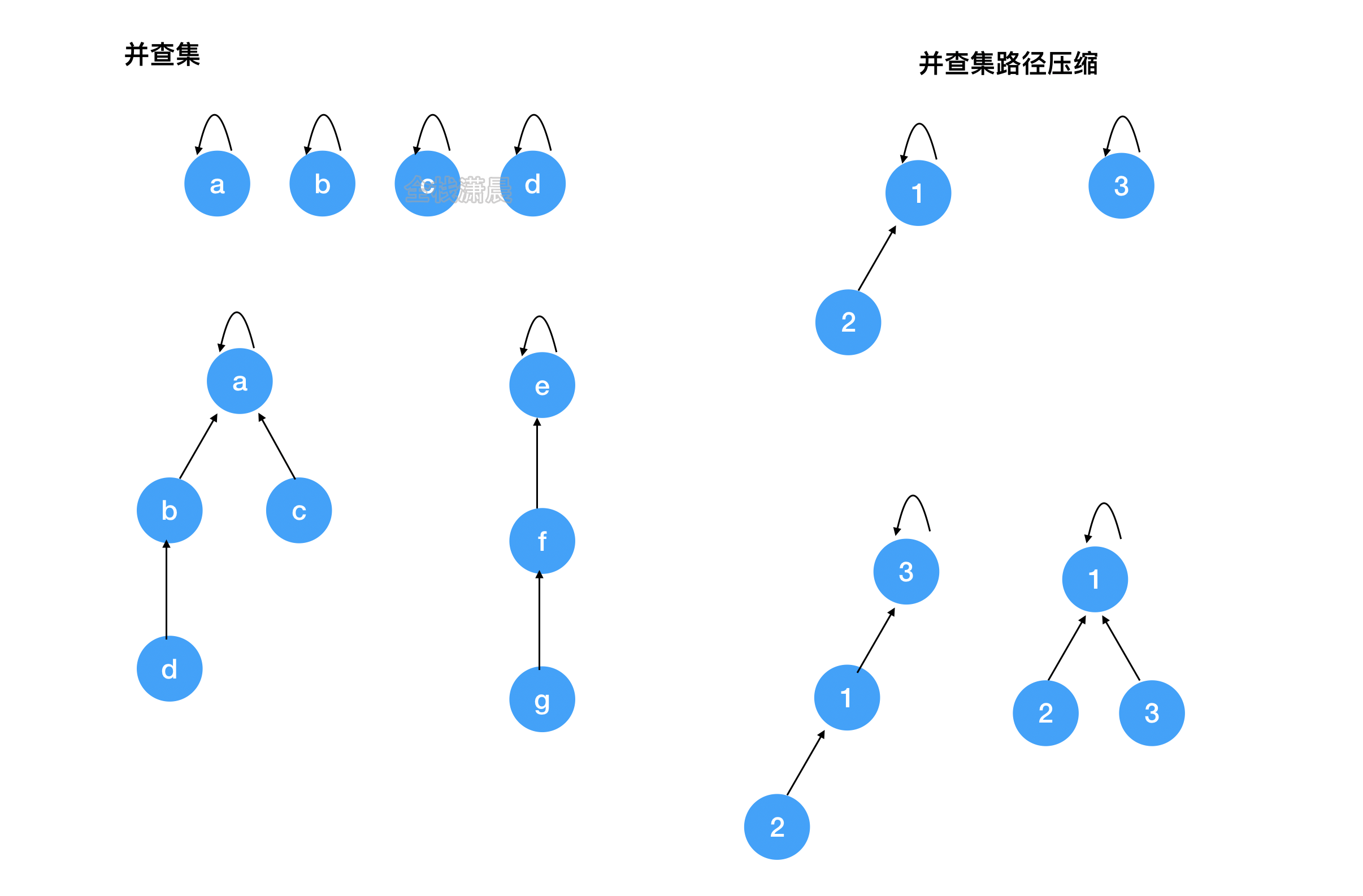
并查集（union & find）：用于处理一些元素的合并和查询问题

Find：确定元素属于哪一个子集，他可以被用来确定两个元素是否属于同一个子集，加入路径压缩，复杂度近乎O(1)

Union：将两个子集合并成同一个集合

ds_88

//                    0,1,2,3
//parent:        0,1,2,3
//size:         1,1,1,1
class UnionFind{
    constructor(n){ //构造一个大小为n的集合
        this.count = n
        this.parent = new Array(n)   
        this.size = new Array(n)  // size数组记录着每棵树的大小
        for (let i = 0; i < n; i++) {
            this.parent[i] = i; // 自己是自己的parent
            this.size[i] = 1;
        }
    }

    union(p,q){ //连通结点p和结点q, p和q都是索引
        let rootP = this.find(p);
        let rootQ = this.find(q);
        if(rootP === rootQ) return
        // 元素数量小的接到数量多的下面，这样比较平衡
        if (this.size[rootP] > this.size[rootQ]) {
            this.parent[rootQ] = rootP;
            this.size[rootP] += this.size[rootQ];
        } else {
            this.parent[rootP] = rootQ;
            this.size[rootQ] += this.size[rootP];
        }
        this.count--;
    }

    isConnected(p, q) { //判断p,q是否连通
        return this.find(p)=== this.find(q) 
    }

    find(x) { //找到x结点的root
        while (this.parent[x] != x) {
            // 进行路径压缩
            this.parent[x] = this.parent[this.parent[x]];
            x = this.parent[x];
        }
        return x;
    }

    getCount() { //返回子集个数
        return this.count;
    }
}

//                    0,1,2,3
//parent:        0,1,2,3
//rank:         1,1,1,1
//采用rank优化
class UnionFind {
    constructor(n) { //构造一个节点数为n的集合
        this.count = n //并查集总数
        this.parent = new Array(n)
        this.rank = new Array(n)  // rank数组记录着每棵树的重量
        for (let i = 0; i < n; i++) {
            this.parent[i] = i; // 自己是自己的parent
            this.rank[i] = 1;    //每个集合上节点的数量
        }
    }

    union(p, q) { //连通结点p和结点q, p和q都是索引
        let rootP = this.find(p);
        let rootQ = this.find(q);
        if (rootP === rootQ) return
        // 深度小的接在深度大元素下
        if (this.rank[rootP] > this.rank[rootQ]) {
            this.parent[rootQ] = rootP;
        } else if (this.rank[rootP] < this.rank[rootQ]) {
            this.parent[rootP] = rootQ;
        } else {
            this.parent[rootP] = rootQ;
            this.rank[rootQ]++
        }
        this.count--;
    }

    isConnected(p, q) { //判断p,q是否连通
        return this.find(p) === this.find(q)
    }

    find(x) { //找到x结点的root
        while (this.parent[x] != x) {
            // 进行路径压缩
            this.parent[x] = this.parent[this.parent[x]];
            x = this.parent[x];
        }
        return x;
    }

    getCount() { //返回子集个数
        return this.count;
    }
}

200. 岛屿数量 (medium)

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1
示例 2：

输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

动画过大，点击查看

方法1.dfs

思路：循环网格，深度优先遍历每个坐标的四周，注意坐标不要越界，遇到陆地加1，并沉没四周的陆地，这样就不会重复计算
复杂度：时间复杂度O(mn), m和n是行数和列数。空间复杂度是O(mn),最坏的情况下所有网格都需要递归，递归栈深度达到m * n

js：

const numIslands = (grid) => {
    let count = 0
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[0].length; j++) {//循环网格
            if (grid[i][j] === '1') {//如果为陆地，count++，
                count++
                turnZero(i, j, grid)
            }
        }
    }
    return count
}
function turnZero(i, j, grid) {//沉没四周的陆地
    if (i < 0 || i >= grid.length || j < 0
        || j >= grid[0].length || grid[i][j] === '0') return //检查坐标的合法性
    grid[i][j] = '0'//让四周的陆地变为海水
    turnZero(i, j + 1, grid)
    turnZero(i, j - 1, grid)
    turnZero(i + 1, j, grid)
    turnZero(i - 1, j, grid)
}

方法2.bfs

思路：循环网格，广度优先遍历坐标的四周，遇到陆地加1，沉没四周的陆地，不重复计算陆地数
复杂度：时间复杂度O(mn),m和n是行数和列数。空间复杂度是O(min(m，n)),队列的长度最坏的情况下需要能容得下m和n中的较小者

js:

const numIslands = (grid) => {
    let count = 0
    let queue = []
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[0].length; j++) {
            if (grid[i][j] === '1') {
                count++
                grid[i][j] = '0' // 做标记，避免重复遍历
                queue.push([i, j]) //加入队列
                turnZero(queue, grid)
            }
        }
    }
    return count
}
function turnZero(queue, grid) {
    const dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]]
    while (queue.length) {//当队列中还有元素的时候 
        const cur = queue.shift() //取出队首元素
        for (const dir of dirs) {//四个方向广度优先扩散
            const x = cur[0] + dir[0]
            const y = cur[1] + dir[1]
            if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] !== '1') {
                continue
            }//检查坐标合法性
            grid[x][y] = '0' //沉没陆地
            queue.push([x, y]) //四周的节点加入队列
        }
    }
}

方法3.并查集

思路：
复杂度：时间复杂度O(mn)，时间复杂度其实是O(mn * f(mn))，f是采用并查集路径压缩时的复杂度，为常数，所以可以忽略。 m和n是行数和列数。空间复杂度是O(mn),并查集的空间

js:

class UnionFind {
    constructor(n) { //构造一个节点数为n的集合
        this.count = n //并查集总数
        this.parent = new Array(n)
        this.size = new Array(n)  // size数组记录着每棵树的重量
        for (let i = 0; i < n; i++) {
            this.parent[i] = i; // 自己是自己的parent
            this.size[i] = 1;    //每个集合上节点的数量
        }
    }

    union(p, q) { //连通结点p和结点q, p和q都是索引
        let rootP = this.find(p);
        let rootQ = this.find(q);
        if (rootP === rootQ) return
        // 元素数量小的接到数量多的下面，这样比较平衡
        if (this.size[rootP] > this.size[rootQ]) {
            this.parent[rootQ] = rootP;
            this.size[rootP] += this.size[rootQ];
        } else {
            this.parent[rootP] = rootQ;
            this.size[rootQ] += this.size[rootP];
        }
        this.count--;
    }

    isConnected(p, q) { //判断p,q是否连通
        return this.find(p) === this.find(q)
    }

    find(x) { //找到x结点的root
        while (this.parent[x] != x) {
            // 进行路径压缩
            this.parent[x] = this.parent[this.parent[x]];
            x = this.parent[x];
        }
        return x;
    }

    getCount() { //返回子集个数
        return this.count;
    }

}

var numIslands = function (grid) {
    let m = grid.length
    if (m === 0) return 0
    let n = grid[0].length
    const dummy = -1
    const dirs = [[1, 0], [0, 1]]//方向数组 向右 向下
    const uf = new UnionFind(m * n)
    for (let x = 0; x < m; x++) {
        for (let y = 0; y < n; y++)
            if (grid[x][y] === '0') {//如果网格是0，则和dummy合并
                uf.union(n * x + y, dummy) 
            }
            else if (grid[x][y] === '1') {//如果网格是1，则向右 向下尝试
                for (let d of dirs) {
                    let r = x + d[0]
                    let c = y + d[1]
                    if (r >= m || c >= n) continue //坐标合法性
                    if (grid[r][c] === '1') { //当前网格的右边 下面如果是1，则和当前网格合并
                        uf.union(n * x + y, n * r + c)
                    }
                }
            }
    }
    return uf.getCount()  //返回并查集的个数减一就行
};

547. 省份数量(medium)

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

方法1.dfs

思路：深度优先遍历，visited记录是否访问过，循环省份数组，递归寻找isConnected矩阵中相邻的城市。
复杂度：时间复杂度O(n^2)，n是城市的数量，遍历矩阵中的每个元素。空间复杂度O(n)，递归深度不超过n

var findCircleNum = function(isConnected) {
  const rows = isConnected.length;
  const visited = new Set();//记录是否访问过
  let count = 0;//省份数量
  for (let i = 0; i < rows; i++) {
      if (!visited.has(i)) {//如果没访问过
          dfs(isConnected, visited, rows, i);//深度优先遍历
          count++;//省份数量+1
      }
  }
  return count;
};

const dfs = (isConnected, visited, rows, i) => {
  for (let j = 0; j < rows; j++) {
      if (isConnected[i][j] == 1 && !visited.has(j)) {//如果i，j相连接
          visited.add(j);
          dfs(isConnected, visited, rows, j);//递归遍历
      }
  }
};

方法2.bfs

思路：广度优先遍历，循矩阵，然后寻找相邻城市加入队列，队列不为空就不断出队，继续遍历
复杂度：时间复杂度O(n^2)，n是城市的数量，遍历矩阵中的每个元素。空间复杂度O(n)，队列和visited数组最长是n

js:

var findCircleNum = function(isConnected) {
  const rows = isConnected.length;
  const visited = new Set();//记录是否访问过
  let count = 0;
  const queue = new Array();
  for (let i = 0; i < rows; i++) {
      if (!visited.has(i)) {//没有访问过
          queue.push(i); //加入队列
          while (queue.length) {//队列不为空 继续循环
              const j = queue.shift();//出队
              visited.add(j);
              for (let k = 0; k < rows; k++) {//循环相邻的城市 加入队列
                  if (isConnected[j][k] === 1 && !visited.has(k)) {
                      queue.push(k);
                  }
              }
          }
          count++;
      }
  }
  return count;
};

方法3.并查集

思路：循环矩阵，遇到相邻的城市就合并，最后返回并查集中集合的数量
复杂度：时间复杂度O(n^2)，n是城市的数量，需要遍历矩阵，经过路径压缩后的并查集中需找父节点复杂度是常数级。空间复杂度是O(n)，即parent的空间

js:

class UnionFind{
    constructor(n){ //构造一个大小为n的集合
        this.count = n
        this.parent = new Array(n)   
        this.size = new Array(n)  // size数组记录着每棵树的大小
        for (let i = 0; i < n; i++) {
            this.parent[i] = i; // 自己是自己的parent
            this.size[i] = 1;
        }
    }

    union(p,q){ //连通结点p和结点q, p和q都是索引
        let rootP = this.find(p);
        let rootQ = this.find(q);
        if(rootP === rootQ) return
        // 元素数量小的接到数量多的下面，这样比较平衡
        if (this.size[rootP] > this.size[rootQ]) {
            this.parent[rootQ] = rootP;
            this.size[rootP] += this.size[rootQ];
        } else {
            this.parent[rootP] = rootQ;
            this.size[rootQ] += this.size[rootP];
        }
        this.count--;
    }

    isConnected(p, q) { //判断p,q是否连通
        return this.find(p)=== this.find(q) 
    }

    find(x) { //找到x结点的root
        while (this.parent[x] != x) {
            // 进行路径压缩
            this.parent[x] = this.parent[this.parent[x]];
            x = this.parent[x];
        }
        return x;
    }

    getCount() { //返回子集个数
        return this.count;
    }
}


var findCircleNum = function(isConnected) {
    const rows = isConnected.length;
    const uf = new UnionFind(rows)

    for (let i = 0; i < rows; i++) {
        for (let j = i + 1; j < rows; j++) {
            if (isConnected[i][j] == 1) {//相邻城市合并
                uf.union(i, j);
            }
        }
    }

    return uf.getCount();
};