数组常用技巧
使用数组代替Map
使用另一个数组来统计每个数字出现的次数,数组的下标作为key, 数组的值作为value,
将数字作为数组的下标索引,数组里的值存储该数字出现的次数,原理有点类似桶排序中使用的计数数组。

比如这里如果1出现了2次,就将索引0的位置存储为2,4出现了1次,就索引3的位置存储为1。

这个做法同样适用于字符串,可以建立一个长度26的整数数组来统计字符串中每个字符出现的次数,前提是只有a-z组成的小写字母(或只有大写字母)

如果是包含大小写字母的字符串,可以使用长度 128 的计数数组,即包含 [A-Z] 和 [a-z] 的ASII码即可。

此题可以用计数数组统计方法,但是空间复杂度不符合 O(1) 要求,如果空间复杂度没有要求的话,完全可以用计数数组。
方法1. 交换到正确的位置:
- 利用数组
[1, 2, ..., N]特性nums[i] = i + 1, 如果nums[nums[i] - 1] != nums[i],就不停交换nums[i] - 1和i位置上的数,最后扫描一遍满足nums[i] != i + 1的数就是重复的。

这里如果是找缺失的,保存的结果是 i + 1 就行
方法2. 置为负数:
- 不断将
index = nums[i] - 1处的数字置为负数,如果该位置已经为负,说明重复, 如果找缺失的就判断正的才置为负数,最终还是正数的就是缺失的
方法3. +N:
- 不断将
index = nums[i] - 1处的数字加n(数组长度),最终大于2n的位置的索引+1就是结果值,如果找缺失的就判断小于等于n
交换数组中的两个数

Java 交换两个数的三种方法:
1.使用一个临时变量暂存两个中的某一个的值

2. 两数相加保存和值

3.两数异或保存

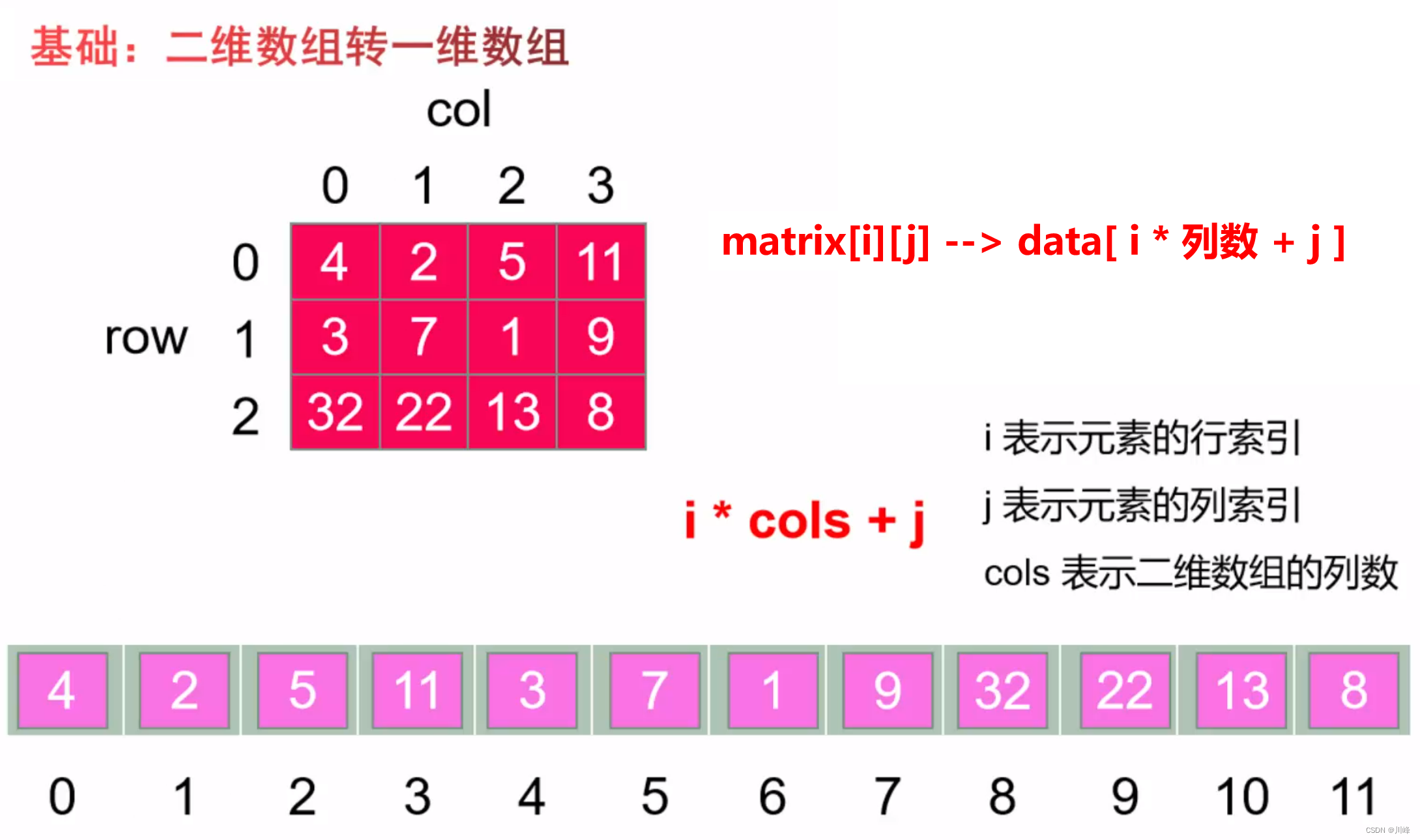
二维数组转一维数组(下标转换)
matrix[i][j] --> data[ i * 列数 + j ]
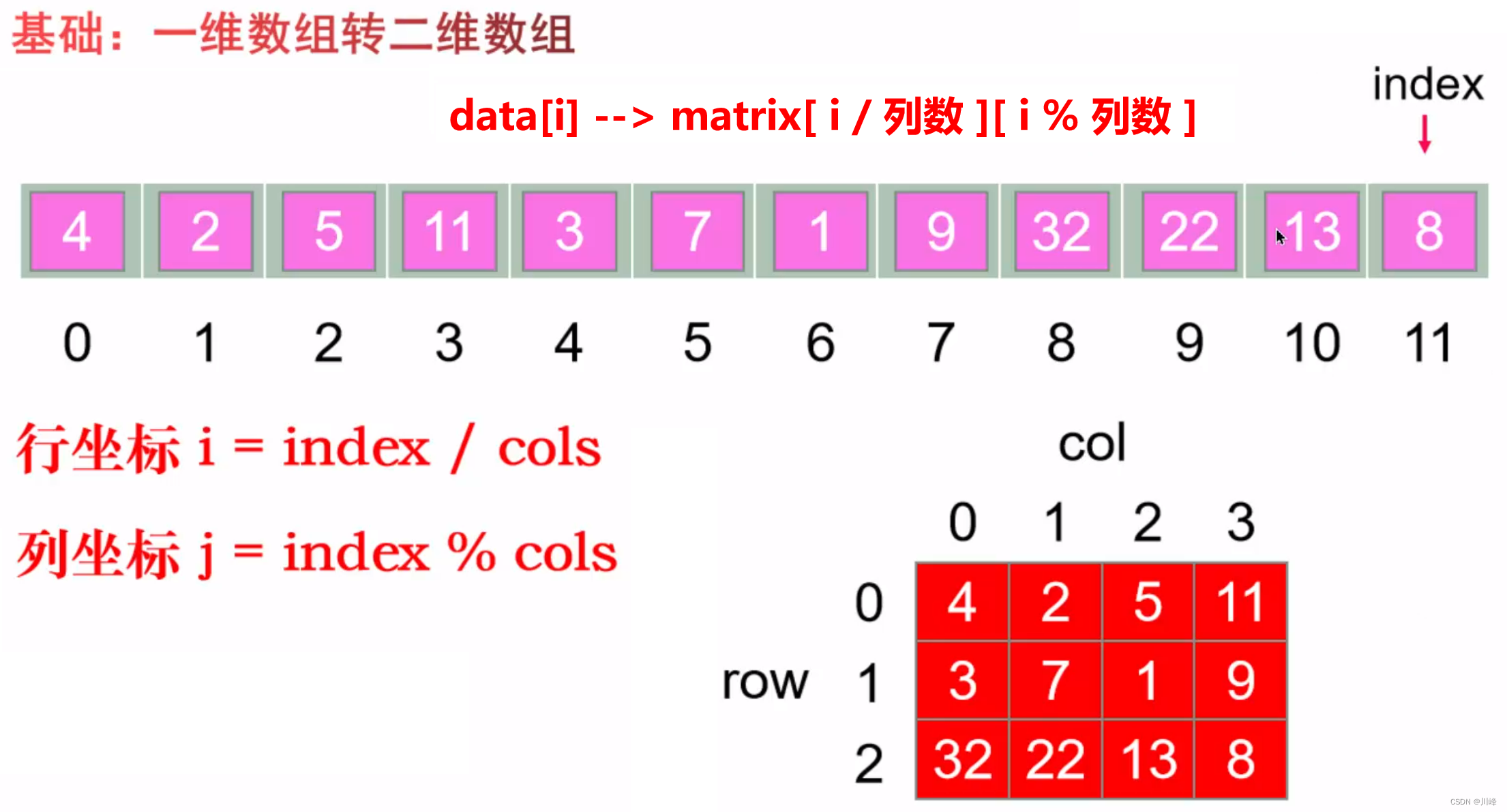
一维数组转二维数组(下标转换)
data[i] --> matrix[ i / 列数 ][ i % 列数 ]
二维数组的四联通(方向数组)
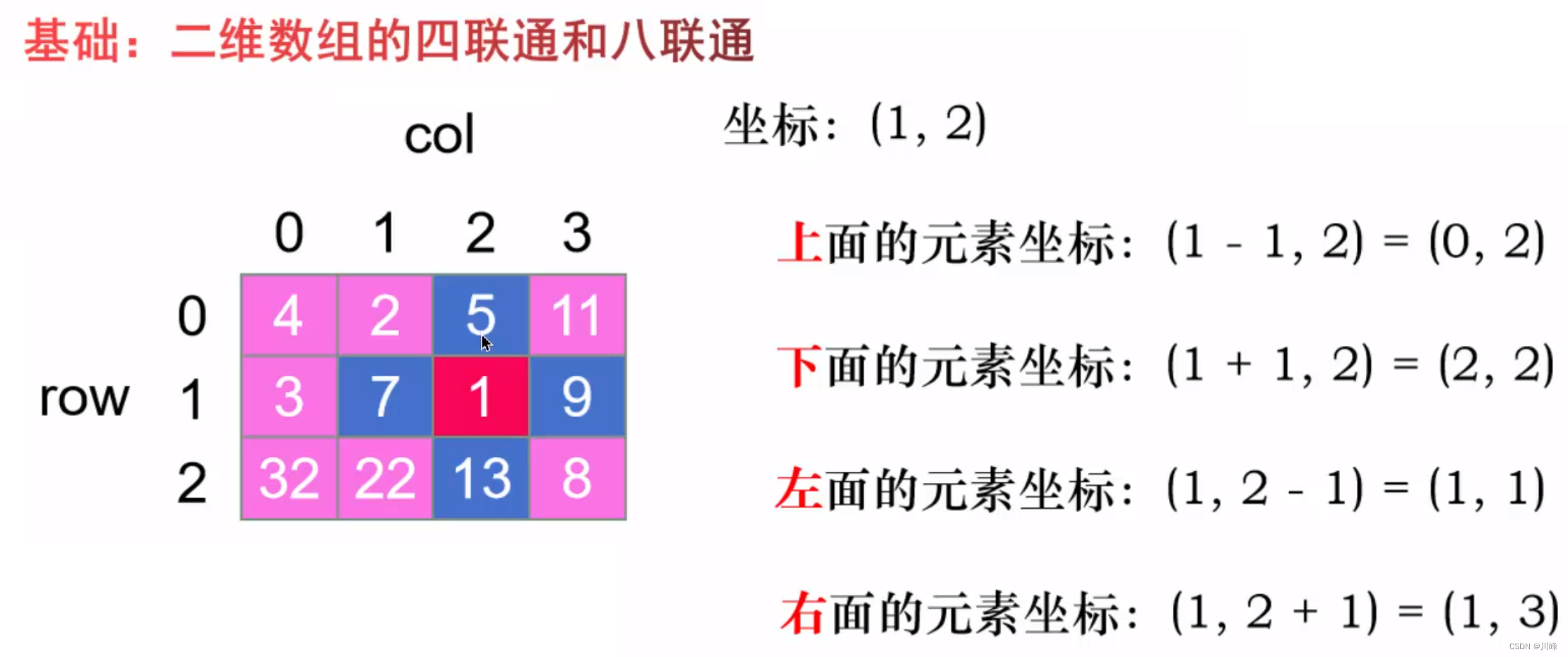
访问二维数组中四个邻居元素的小技巧:directions数组

这个技巧在一些二维矩阵题目的DFS和BFS解法中经常使用到。
二维数组的八联通(方向数组)
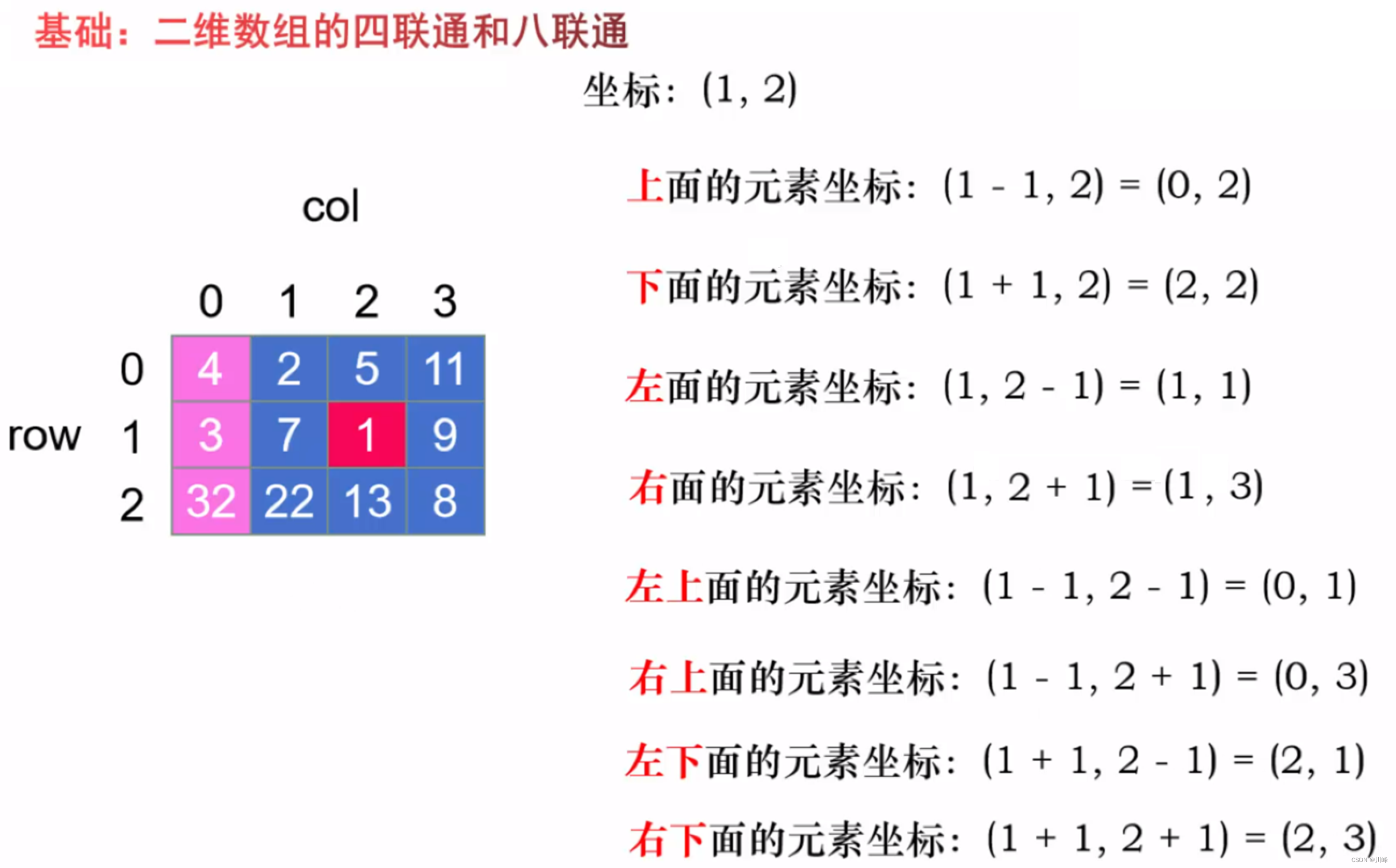

注意防止下标访问越界问题:
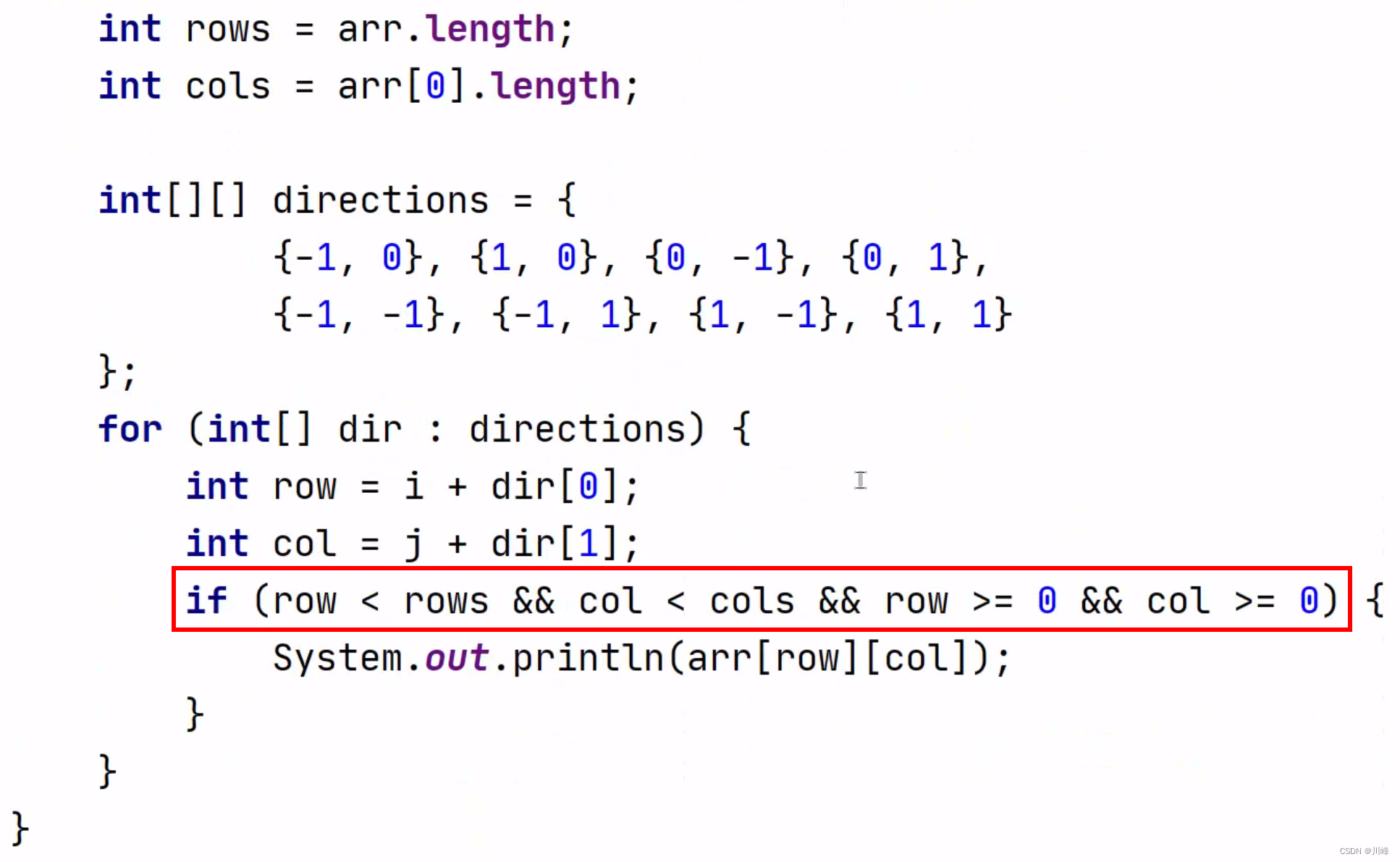
Java 内置List、数组、Map等常用方法
这里只是列出一些在刷题过程中可能用到的,或者说比较有用的Java Api 方法,这些方法在平时开发中我们并不需要特别的关心或记忆,因为有IDE工具快捷提示。但是对于刷题而言,通常面对的是白板,界面没有提示功能,所以可能很难想的起来,因此有必要熟悉一下。


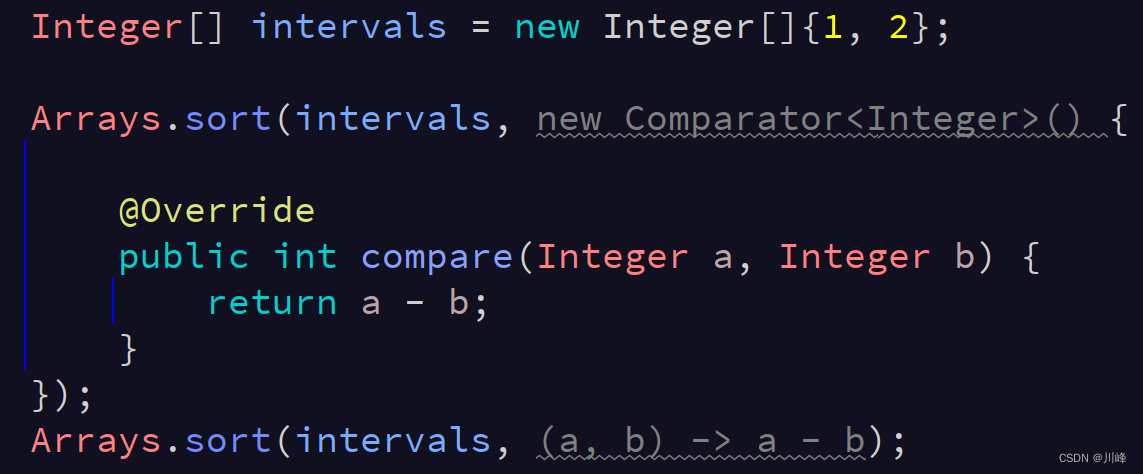
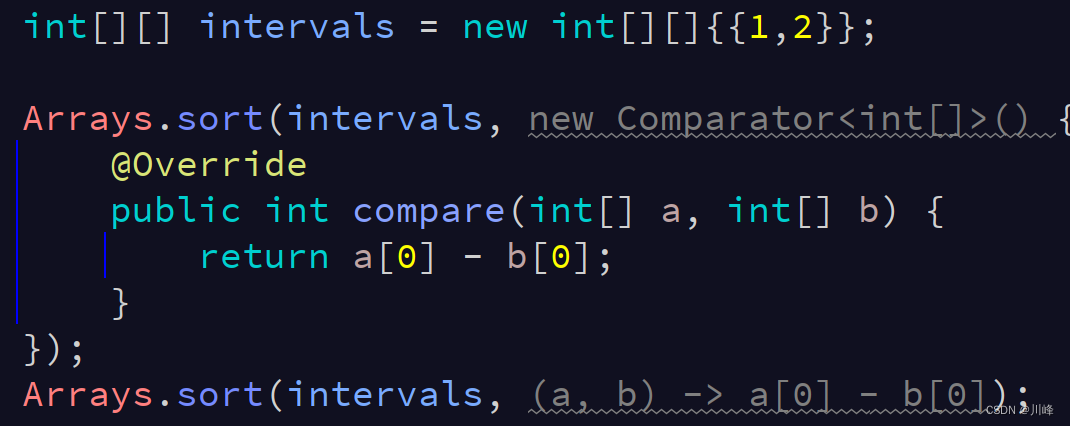


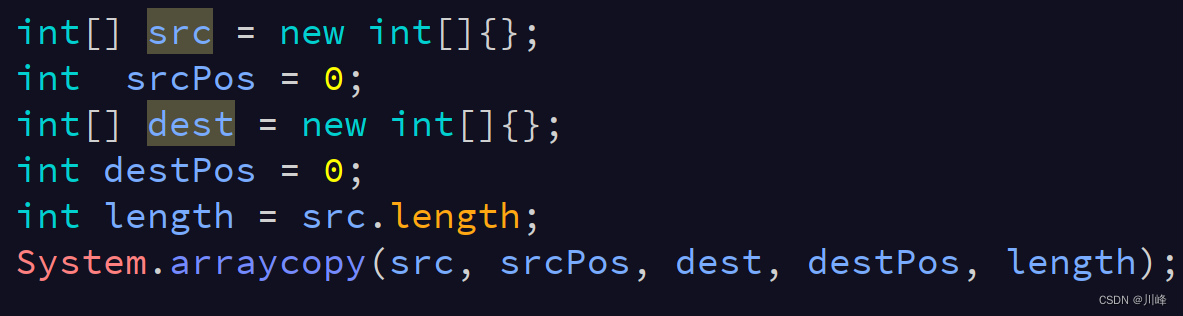






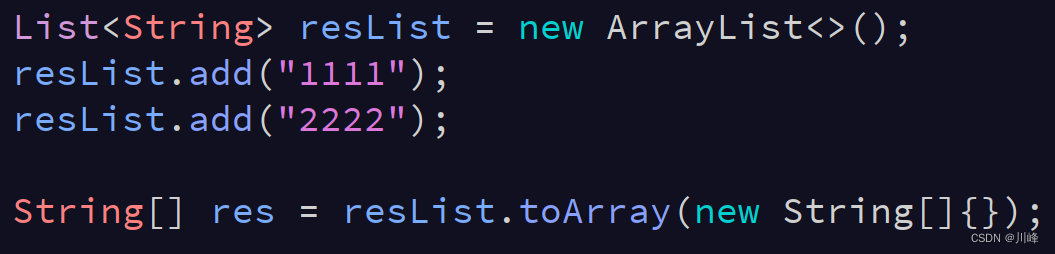


这个传Deque也可以,只要是Collection接口的实现类都可以。
位运算技巧
获取整型二进制中固定高位/低位的值:
-
拿到二进制的低16位:n & 0xFFFF
-
拿到二进制的高16位:n & 0xFFFF0000
-
同理,取低4位和0xF相与,取低8位和0xFF相与,或拿到低/高x位等类似,只需要与上对应位上是1其余位上是0的数即可。
-
n & 1 可以取出最低位的值(1或0),可用来计算 n 中 1 的个数,或者用来判断奇偶数(偶数最低位是0,奇数最低位是1)
判断第 i 位是否是 1:
-
n & (1 << i)!= 0 (这里 i 从 0 开始,如果是for循环处理,应该是枚举[0, 31])
-
(n >> i) & 1 != 0 或 (n >> i) & 1 == 1 (这里 i 枚举范围同样是 [0, 31])
其中 n & (1 << i)的结果,只能判断不等于 0 才是这一位是1,不能判断等于1,因为此时对应的十进制不一定是1。而 (n >> i) & 1 的结果要么是1 要么是0,因此可以直接判断等于1,也可以直接判断不等于0。
去掉或只保留最后一位的 1:
-
去掉最后一位的 1:n & (n - 1) 即将最后一位的1置为0了, 可用来判断2的幂(只有最高位上是1)
-
只保留最后一位的 1:n & -n 或 n & (~n + 1) 注意:是得到只含有最后一位上1的数,但并不是十进制的1
异或的三个性质:
-
任何数和 0 异或还是自身:a ^ 0 = a
-
相同的数异或为 0:a ^ a = 0
-
交换律:a ^ b ^ c = a ^ c ^ b
另外补充一个:任何数和 1 异或的效果是将最低位取反,对于偶数来说 a ^ 1 = a + 1,对于奇数来说 a ^ 1 = a - 1
使用异或代替加法运算:
a ^ b:效果等于 a 和 b 的二进制无进位的相加结果
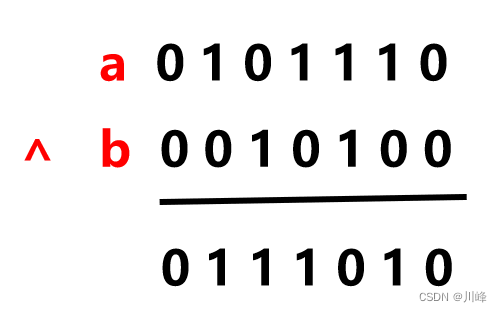
(a & b) << 1:效果等于 a 和 b 的二进制按位相加的进位值
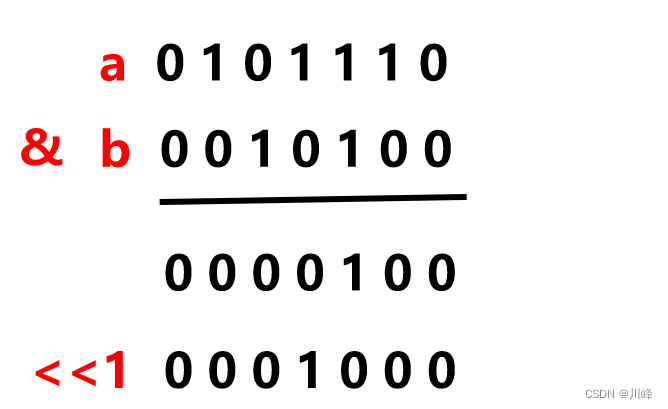
无符号右移>>>和普通右移>>的区别:无符号右移高位补0,普通右移高位补符号位(符号位是1就补1,符号位是0就补0)
如何设置指定二进制位上的值:
-
n | (1 << i) 可以将 n 的第 i 位置为 1 (这里 i 枚举范围是 [0, 31])
-
n & ~(1 << i) 可以将 n 的第 i 位置为 0
位图
常见题目:如何快速查找一千万个整数中是否包含某个整数,每个整数大小在0到1亿范围内
使用位图结构,存储海量数据。

比如可以使用 8 个二进制位来表示 [0, 7] 范围内的数字是否存在,对应数字下标的二进制位上是 1 表示该数存在,是 0 表示该数不存在。
或上 1 << num 的结果是将第num位置为 1:

与上 1 << num 的结果,可以判断num是否存在,结果为1说明该数存在,否则为0说明不存在:

如果是一千万个整数,则使用byte数组:


即一个比特位上的1或0对应一个整数是否存在,一千万个整数就使用一千万个比特位,一千万数量级Byte内存占用大概是 1MB 左右,而一亿数量级Byte内存占用大概是 12MB 左右。
测试代码:

注意上面代码中构造函数中除以了8,传入100,000,000,得到的是一个长度12,500,001的byte数组,但是由于byte数组中的1个byte能表示8个数字的有无,实际上可以表示1亿个整数。
另一种实现:

布隆过滤器
布隆过滤器是什么
- 布隆过滤器是一种占用空间很小的数据结构,它由一个很长的二进制向量和一组Hash映射函数组成,它用于检索一个元素是否在一个集合中,空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。
布隆过滤器原理是?
- 假设我们有个集合 A,A 中有 n 个元素。利用 k个哈希散列函数,将 A 中的每个元素映射到一个长度为 a 位的数组 B 中的不同位置上,这些位置上的二进制数均设置为 1。如果待检查的元素,经过这 k 个哈希散列函数的映射后,发现其 k 个位置上的二进制数全部为 1,这个元素很可能属于集合 A,反之,一定不属于集合 A。
来看个简单例子吧,假设集合 A 有 3 个元素,分别为 {d1,d2,d3}。有 1 个哈希函数,为 Hash1。现在将 A 的每个元素映射到长度为 16 位数组 B。
假如 d1, d2 在映射时没有冲突, 接着我们把 d3 也映射过来,假设 Hash1(d3) 也等于 2,它也是把下标为 2 的格子标 1:
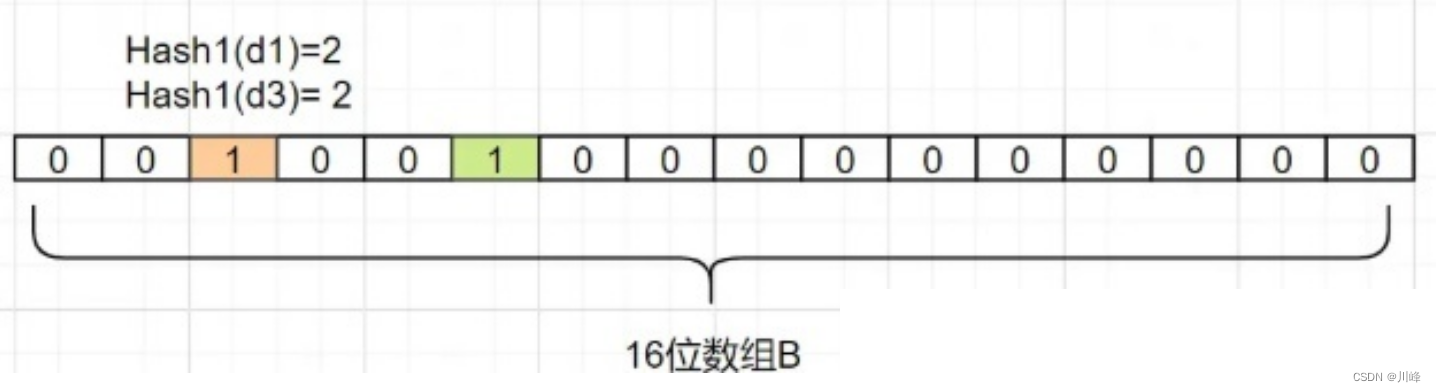
因此,我们要确认一个元素dn是否在集合A里,我们只要算出 Hash1(dn) 得到的索引下标,只要是 0,那就表示这个元素不在集合 A,如果索引下标是 1 呢?那该元素可能是 A 中的某一个元素。因为你看,d1 和 d3 得到的下标值,都可能是 1 ,还可能是其他别的数映射的,布隆过滤器是存在这个缺点:会存在hash碰撞导致的假阳性,判断存在误差。
如何减少这种误差呢?
- 搞多几个哈希函数映射,降低哈希碰撞的概率
- 同时增加B数组的bit长度,可以增大hash函数生成的数据的范围,也可以降低哈希碰撞的概率
布隆过滤器简单讲就是二进制数组+哈希函数,优点是省空间效率高,缺点:只能准确的判断一个数不在集合中,但不能准确的判断一个数在集合中(哈希冲突导致的误判率)
在实际工作中,布隆过滤器常见的应用场景如下:
- 网页爬虫对 URL 去重,避免爬取相同的 URL 地址;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
- Google Chrome 使用布隆过滤器识别恶意 URL;
- Medium 使用布隆过滤器避免推荐给用户已经读过的文章;Google BigTable,Apache HBbase 和 Apache Cassandra 使用布隆过滤器减少对不存在的行和列的查找。
进一步加深对位运算的理解:
我们知道在HashMap的构造函数中会传入初始容量和加载因子(加载因子默认0.75,当容量达到75%时,会进行扩容),如果不传入初始容量,则默认容量是16,如果设置了容量,会找到与之最接近的2的幂,如 2 4 6 8 16 32,如果传15会变成16,这是通过如下代码计算的:
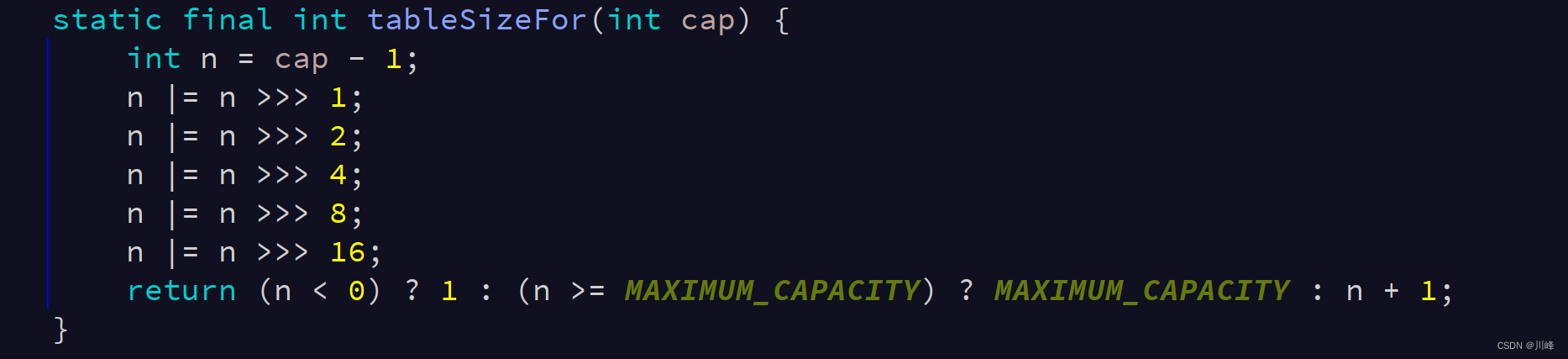
这里 n 先将传入的容量 -1,然后通过 n 不断的和 n 分别右移 1 2 4 6 8 16位的结果进行或运算,最后再 +1,其实得到的就是大于n且与n最接近的二进制,之所以要这样的值是因为HashMap在定位key时,需要进行数组取余,而计算机进行位运算比%取余速度快,因此需要数组的长度是2的幂。
下面分析这段代码具体是如何得到大于n且与n最接近的二进制的:

根据题目数据量猜解法
一般对于时间复杂度是10^8级别的算法不同开发语言的时间限制如下:
- C/C++:1s
- Java: 2~4s
所以如果选择的算法时间复杂度为 O(n^2) 就会有超时的风险,此时我们可以看题目给出的数据量 N 的规模进行猜测:
-
如果题目给出的数据量是10^6,说明至少是 O(nlogn) 或 O(n) 的时间复杂度内解决,因为如果是 O(n^2) 会超过10^8
-
如果题目给出的数据量是10^3,说明可以使用 O(n^2) 时间复杂度也不会超过 10^8
-
如果题目给出的数据量是10^12,说明可能需要二分或数据本身上做文章,因为本身直接遍历就超过 10^8
但如果面试中没有给出数据量,那就不好猜了。
一些常见的解题算法手段
1.直接模拟 -> 解决
2.暴力解法 -> 时间复杂度很高,这可能是因为:
- 1)选择错了数据结构,比如 ArrayList --> HashSet
- 2)存在大量的重复计算,这时需要消除重复计算:a. 预计算,b. 动态规划
预计算的常见手段:
-
前缀和
-
排序:
- 1) 二分查找 -> O(logn)
- 2) 相同的元素会在一起,有的时候可以降低时间复杂度,比如排序去重
-
构建哈希表 -> 哈希查找 -> O(1)
查找算法常见手段:
- 堆查找 -> O(1)
- 使用栈辅助查找,因为栈顶的操作的时间复杂度是 O(1)
- 双指针(快慢指针、对撞指针、滑动窗口等)
Master公式
形如 T(N)=a*T(N/b)+O(N^d)(其中的a、b、d都是常数)的递归函数,可以直接通过Master公式来确定时间复杂度
-
如果 log(b,a)<d,复杂度为O(N^d)
-
如果 log(b,a)>d,复杂度为O(N^log(b,a))
-
如果 log(b,a)==d,复杂度为O(N^d*logN)
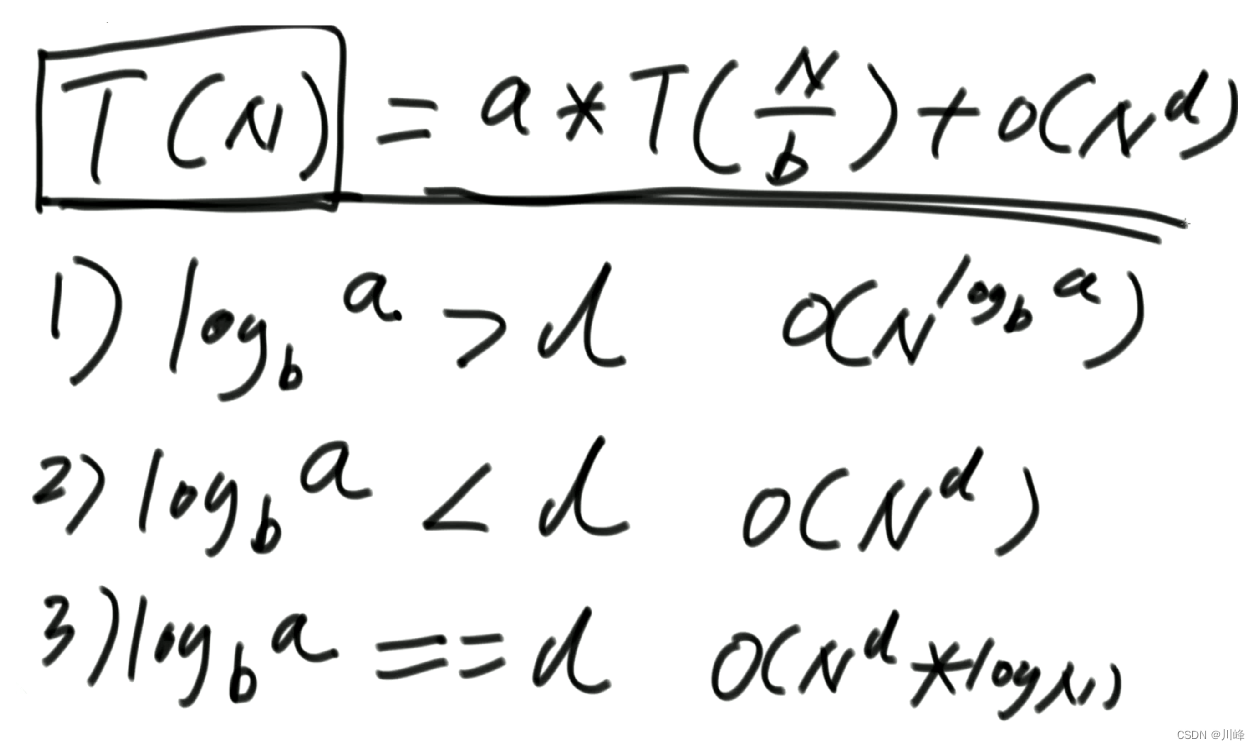
例如下面的例子时间复杂度跟for循环求一样都是O(N)
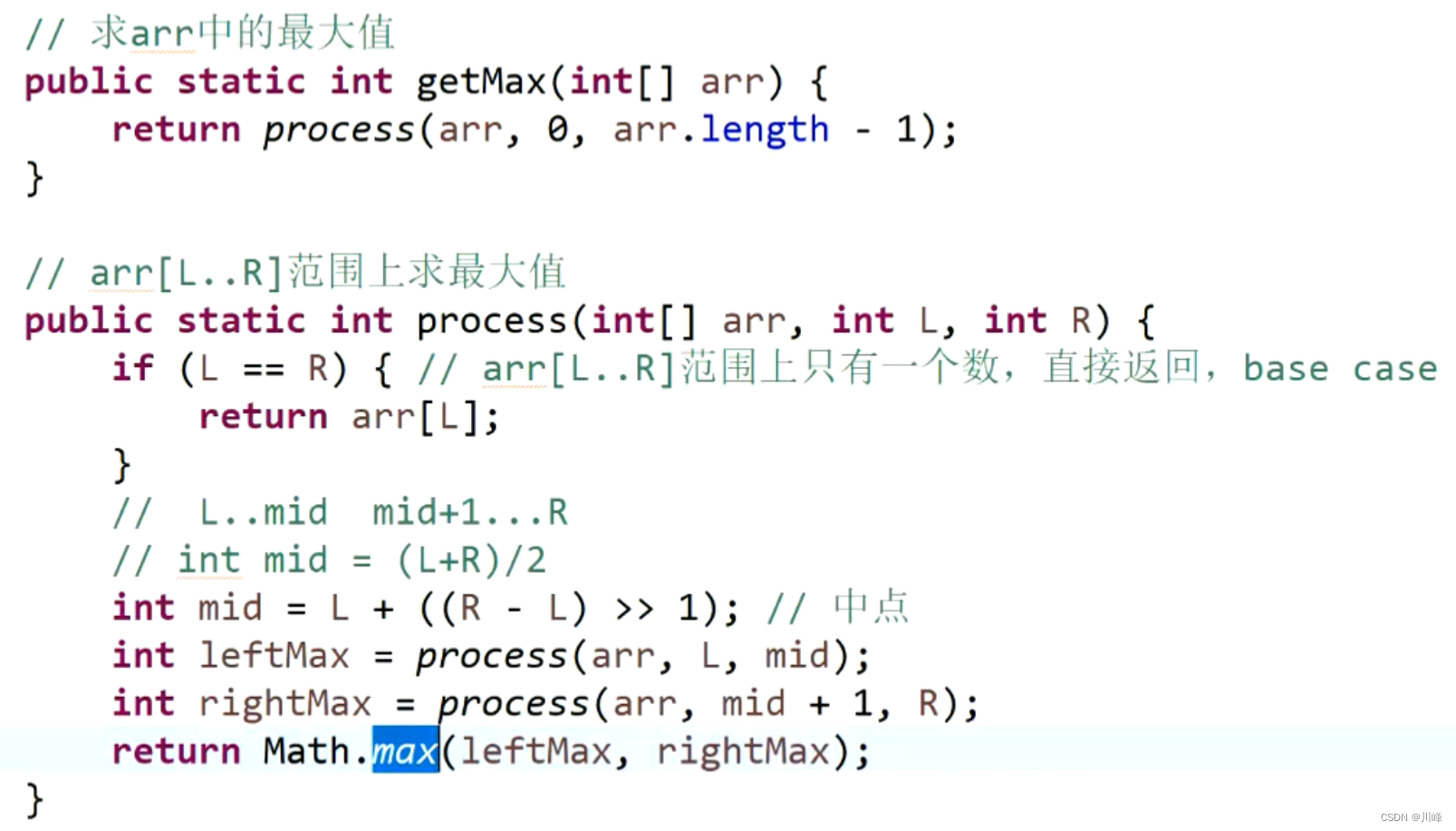
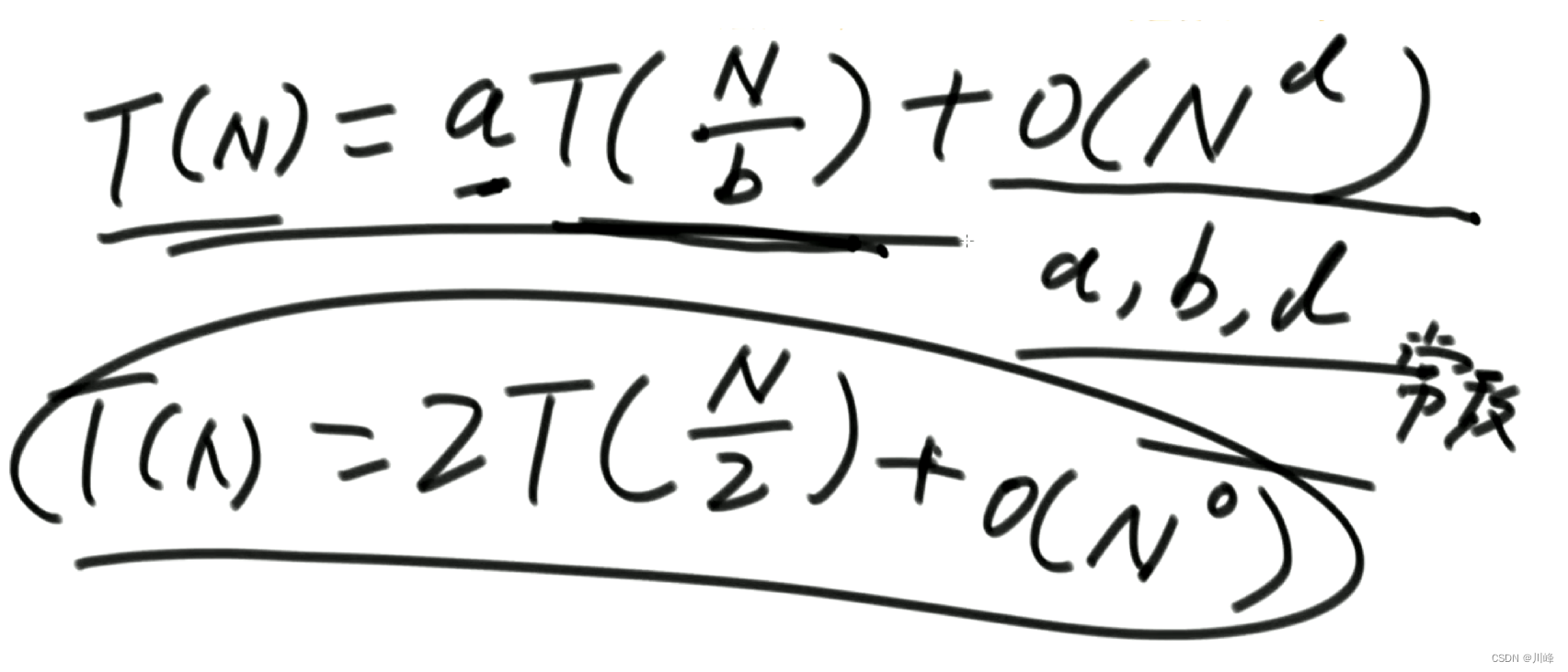
其中a表示调用了2次递归,b表示每次递归处理的规模是N/2,d表示除去递归调用之外其余的代码时间复杂度,由于是常数O(1),所以这里是O(N^0)
ASCII码对照表
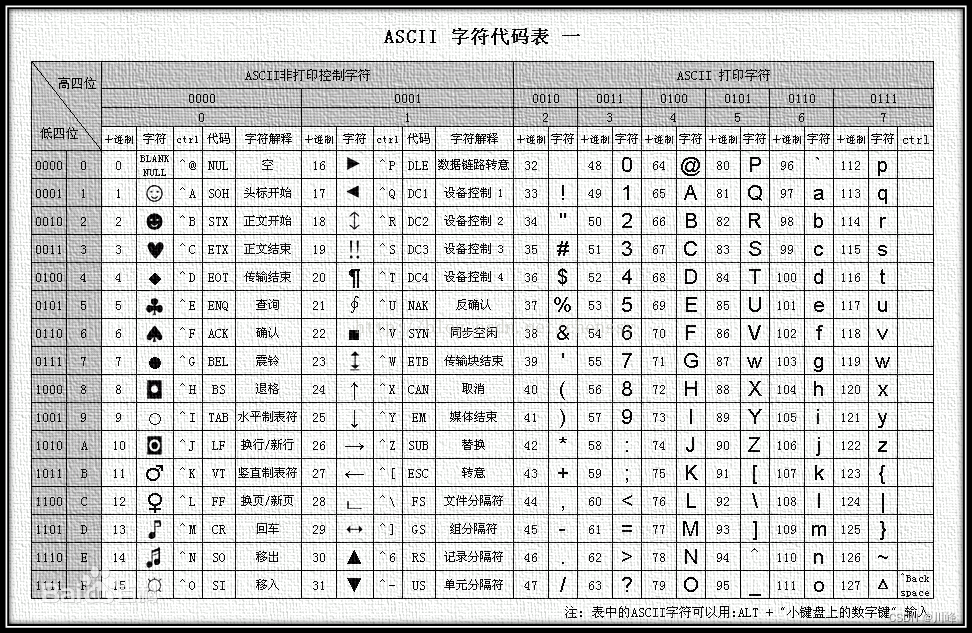
在处理一些字符串类的题目时,可能会涉及到这个表,一般是在定义计数数组的情况下,但是不需要记住,只需要了解该表中 [A-Z] 的范围 [65, 90] 的在 [a-z] 的范围 [97, 122] 的前面,且小写字母的ASCII码要比大写字母的ASCII码值大32。
如果字符串只包含大写/小写字母的字符串可考虑使用长度26的计数数组,都包含的可用直接使用长度128的计数数组。
最大公约数公式
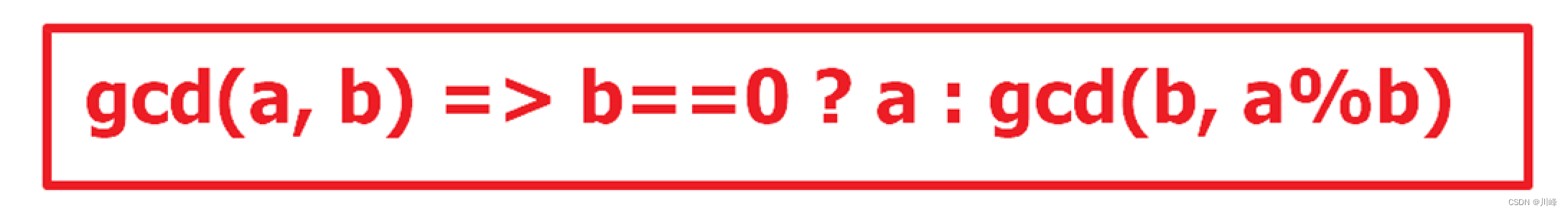

记住即可,部分题目中会涉及到。
卡特兰数

该表达式称为卡特兰数。 如力扣【96. 不同的二叉搜索树】就是卡特兰数的应用。
高斯求和公式 等差数列公式
高斯求和公式:
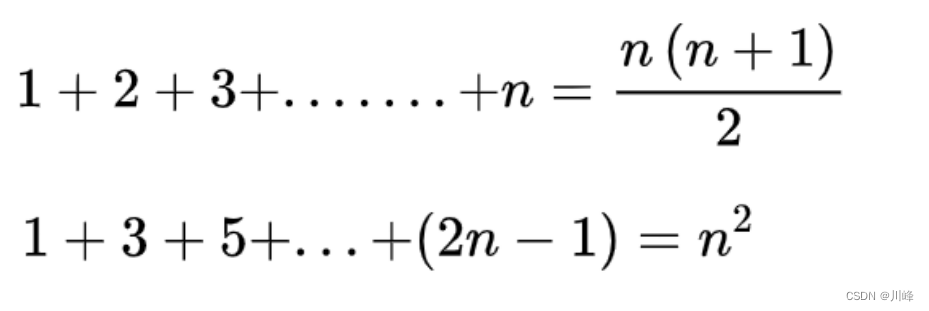
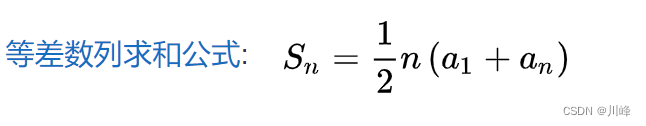
排列组合公式
排列公式(方法数乘法原理):
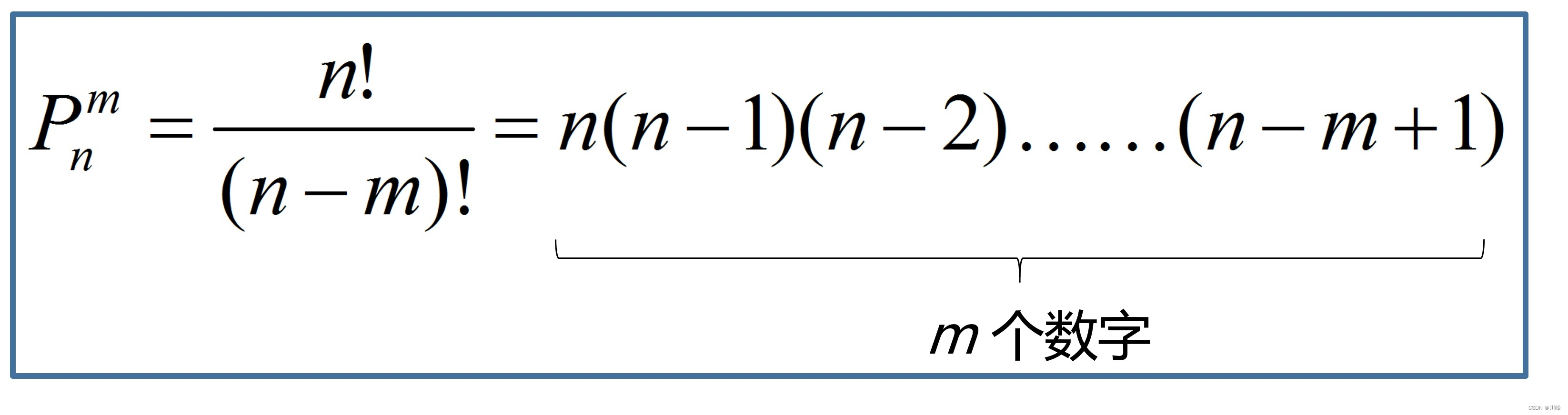

排列是顺序相关的,总共有 6 种:AB、AC、BA、BC、CA、CB
组合公式(组合种类):
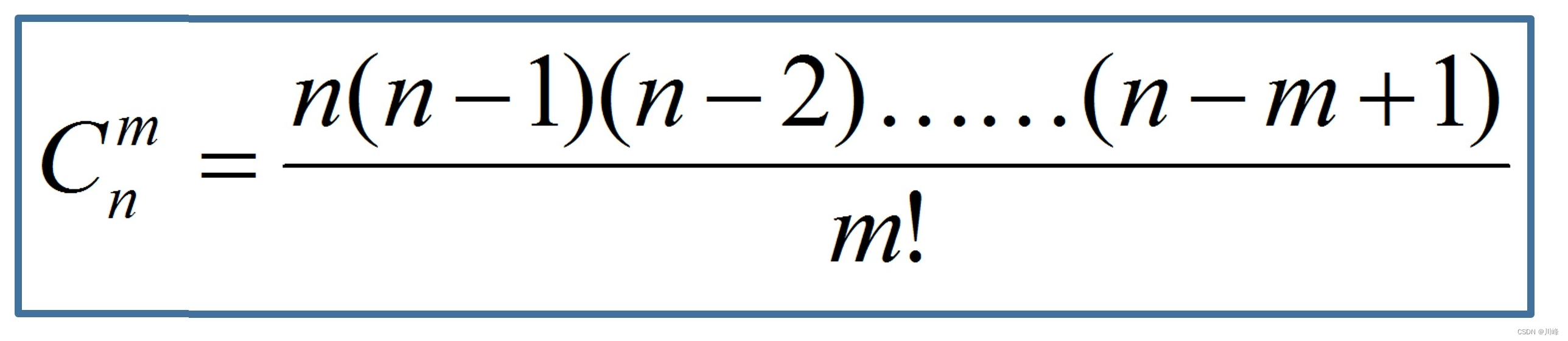
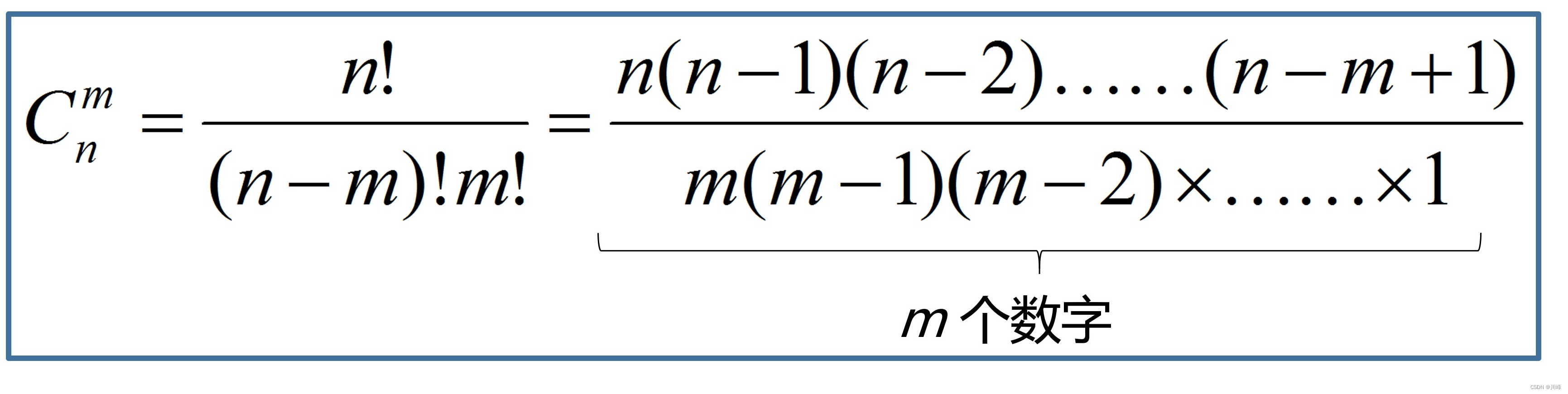
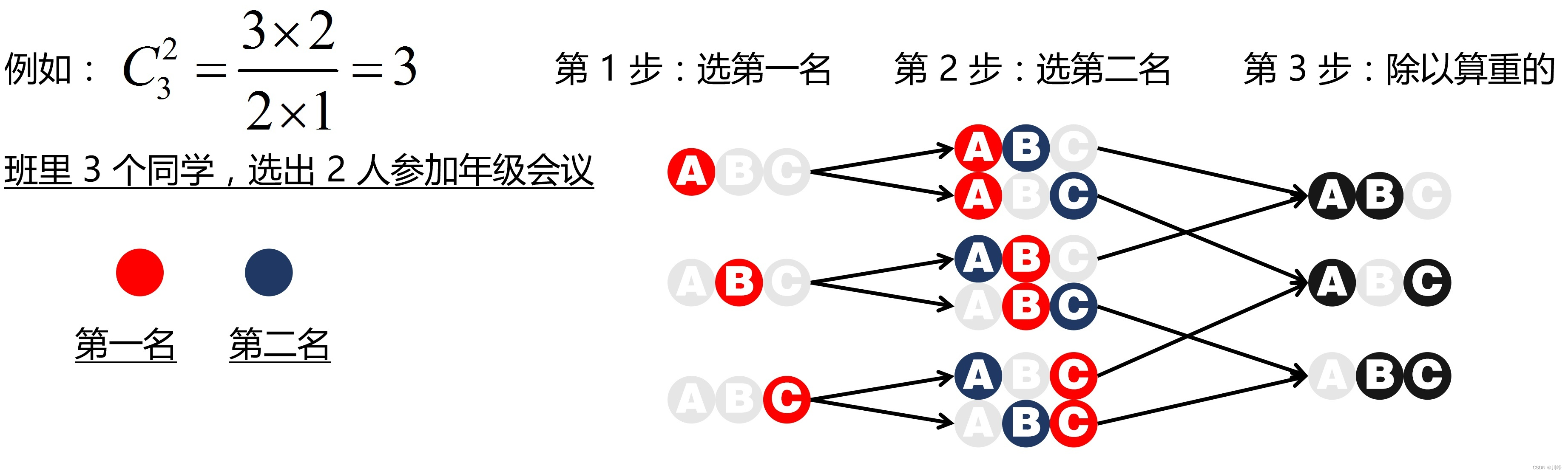
组合是顺序无关的,总共有 3 种:AB、AC、BC
缓存算法
-
FIFO:淘汰最先放入缓存的数据,即 FIFO (First In First Out)缓存
-
LRU :淘汰最久未使用的数据,即 LRU (Least Recently Used)缓存
-
LFU:淘汰最不频繁使用的数据,即 LFU(Least Frequently Used)缓存
FIFO 算法可采用 HashMap + Queue 实现,其中 HashMap 存储数据,Queue 维护键值对的顺序。
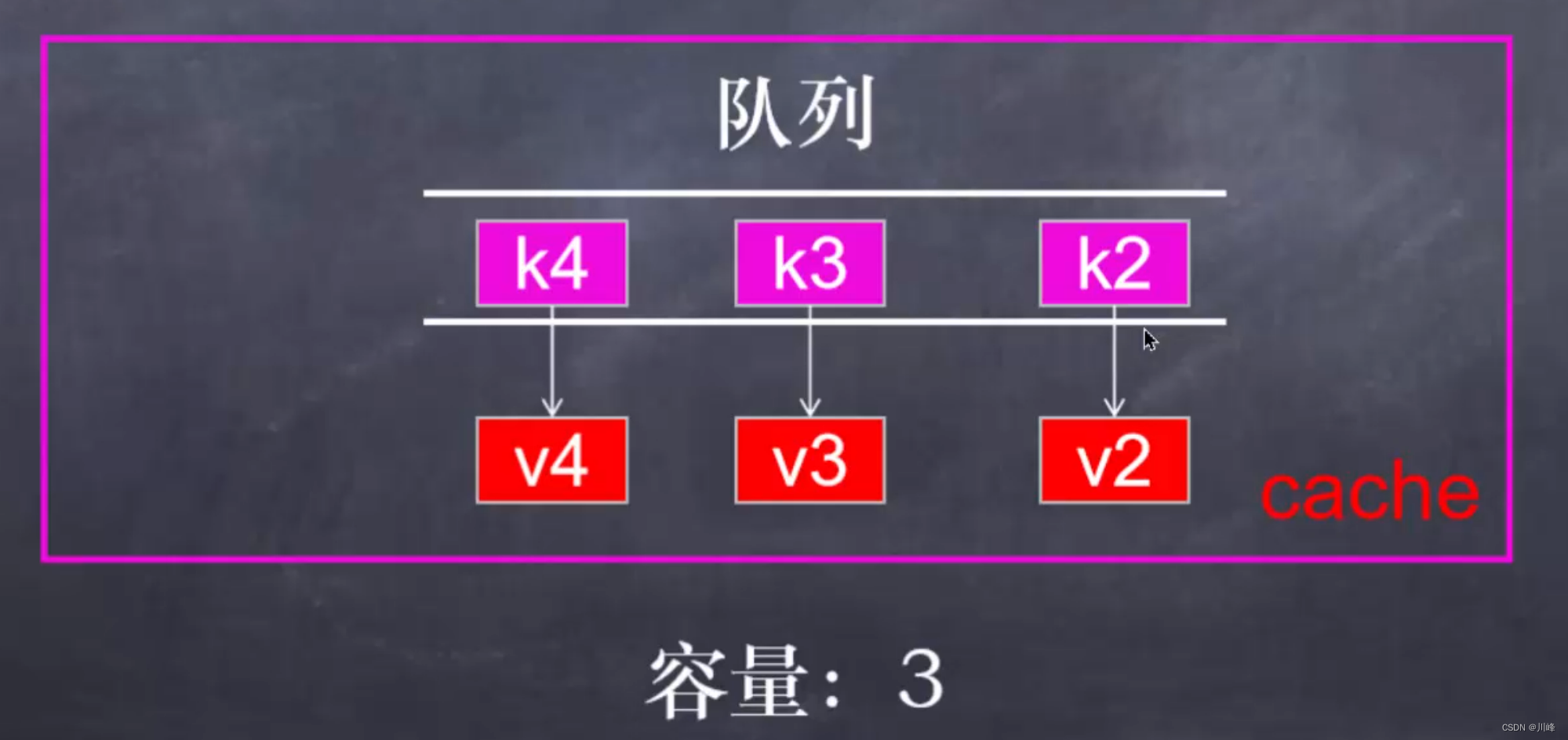

LRU是最近最少使用的先淘汰,即最久未使用的淘汰,可使用双向链表 + HashMap来实现,其中 HashMap 存储数据,双向链表维护键值对的顺序。
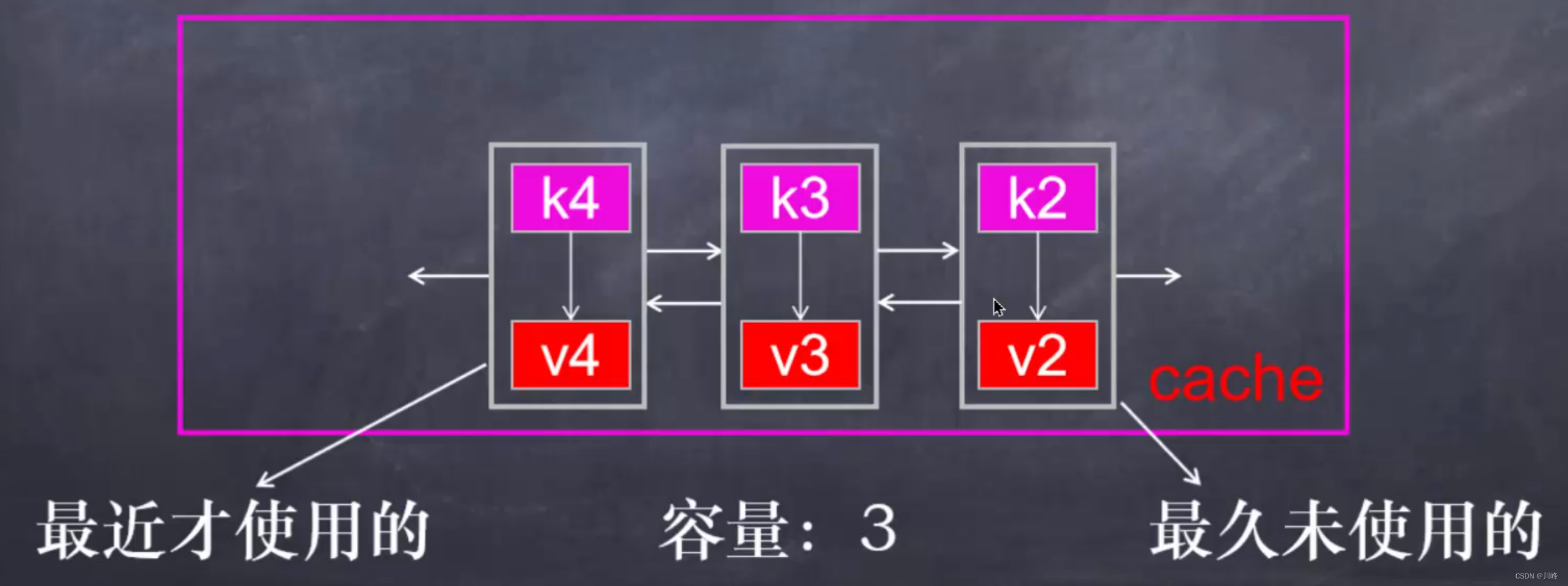
通过双向链表的表头维护最近使用过的节点,通过双向链表的表尾维护最近未使用过的节点,每次访问节点时(map的get/put操作),将节点移动到双向链表的表头。
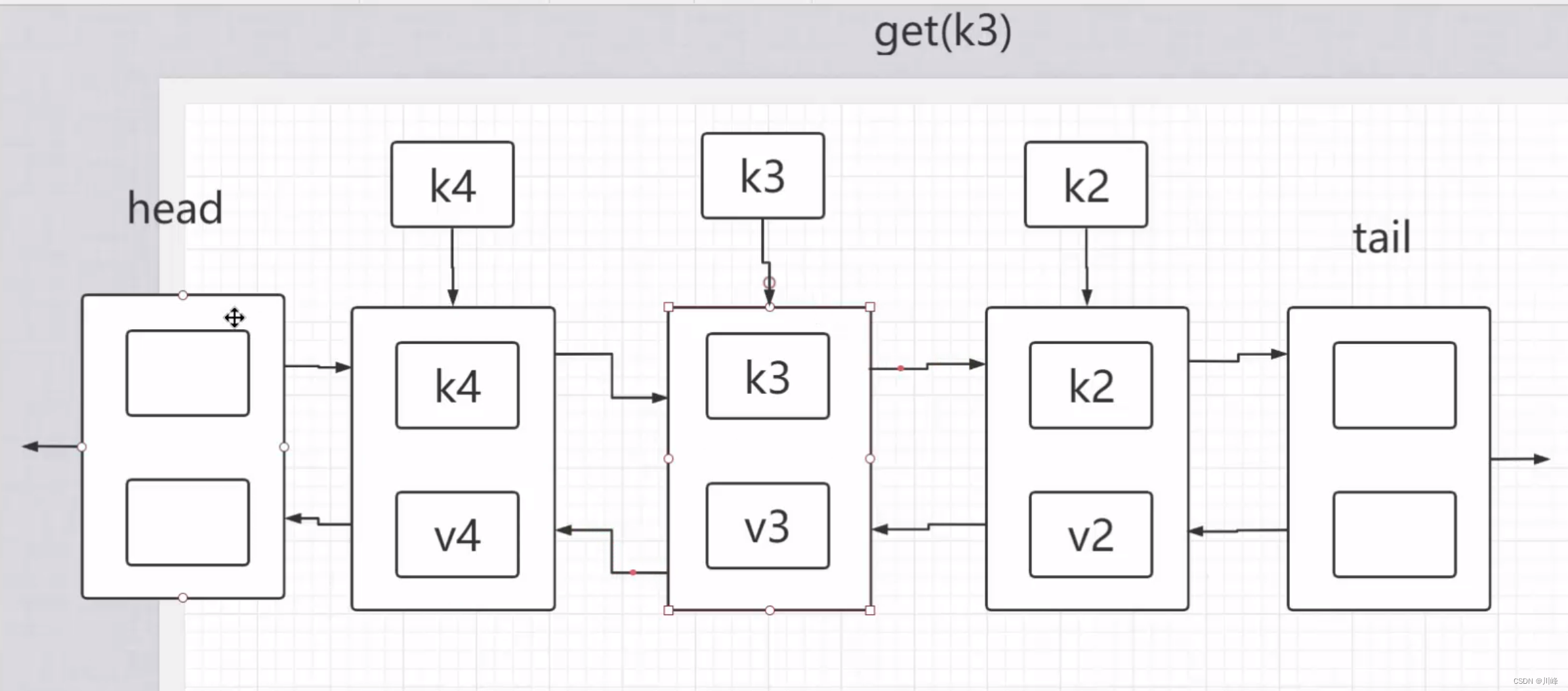
可使用Java内置的LinkedHashMap实现LRU,LinkedHashMap就是采用HashMap+双向链表的实现,默认是按照put的顺序来排序的,LinkedHashMap和HashMap的主要区别就是前者可以按访问操作排序,后者是无序的。
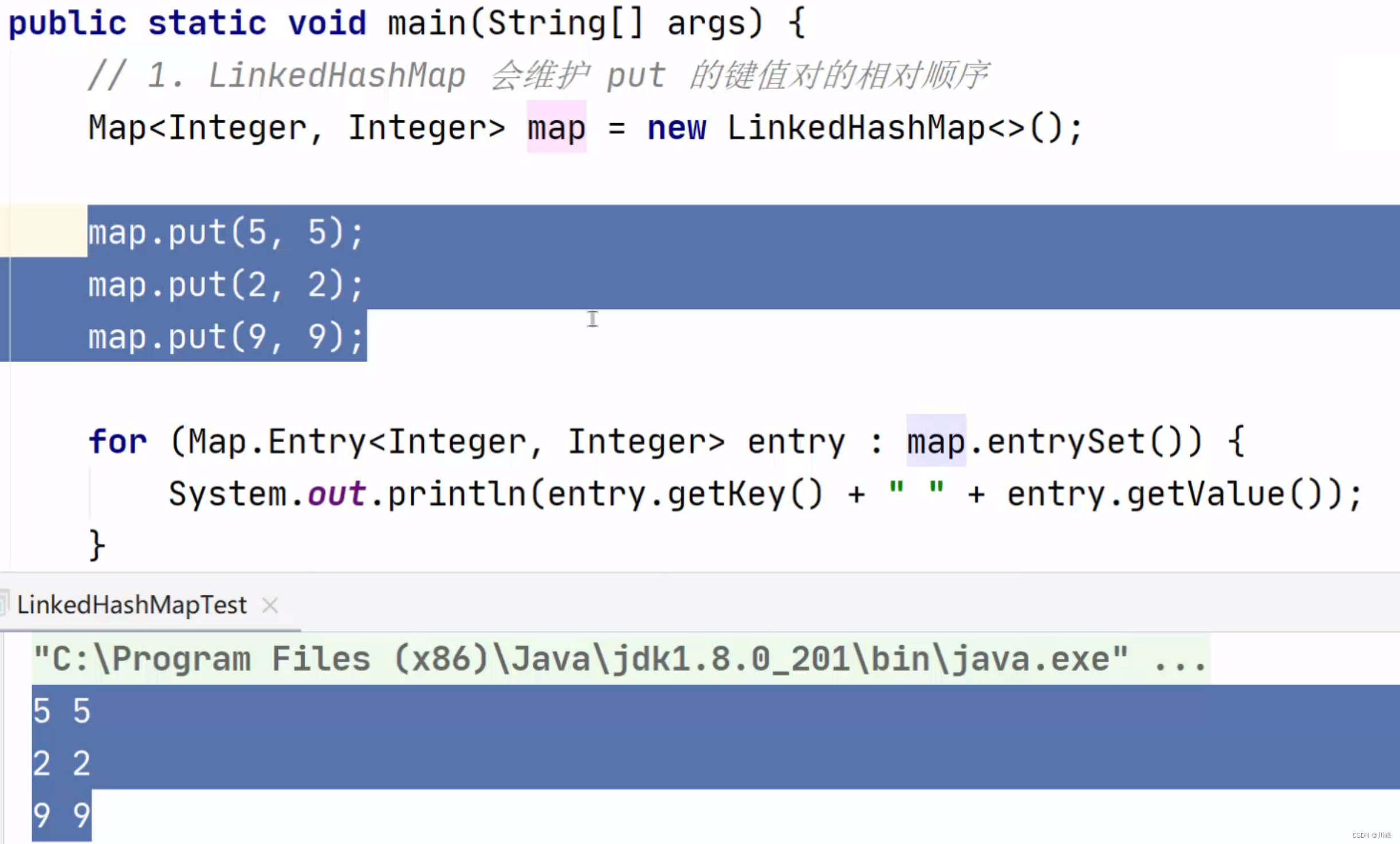
LinkedHashMap 默认是按照插入顺序 (put) 排序的,构造函数的第三个参数传true可以实现按访问顺序 排序。按访问顺序时,最近使用过的在表尾,表头是最久未使用的。

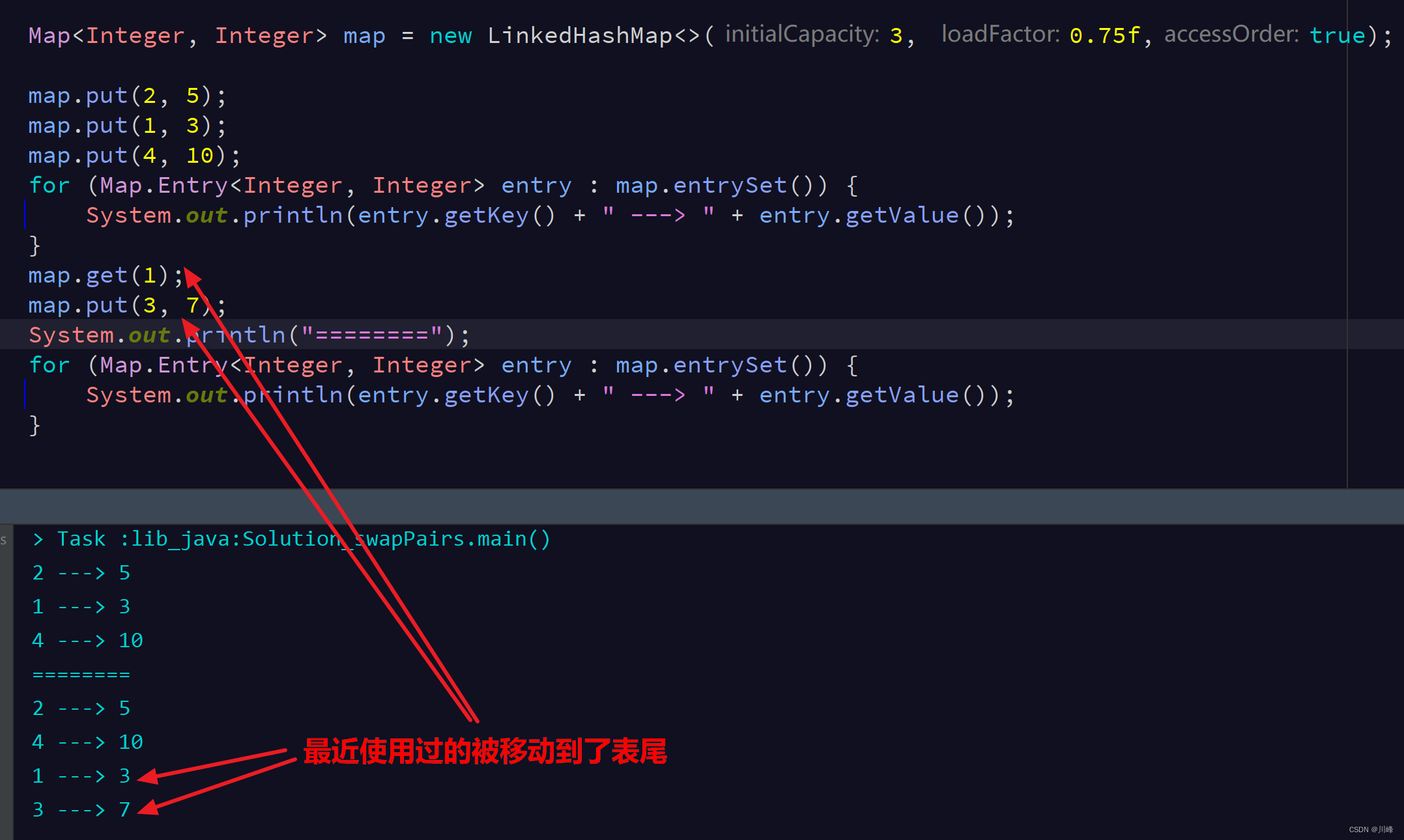
实现LRU只需要继承LinkedHashMap即可

其中 removeEldestEntry 表示要不要删除最老的数据,返回true表示要删除
LeetCode 146 实现方式:

LFU 是使用次数最少的淘汰,如果访问次数一致,最久未访问的那个淘汰。