文章目录
- 前言
- 1. 层次遍历介绍
- 2. 基本的层次遍历与变换
- 2.1 二叉树的层次遍历
- 2.2 层次遍历-自底向上
- 2.3 二叉树的锯齿形层次遍历
- 2.4 N叉树的层次遍历
- 3. 几个处理每层元素的题目
- 3.1 在每棵树行中找出最大值
- 3.2 在每棵树行中找出平均值
- 3.3 二叉树的右视图
- 3.4 最底层最左边
- 总结
前言
提示:这个世界上的任何一次拥抱都是将以松手告终。 --约瑟夫·布罗茨基《悲伤与理智》
二叉树的层次遍历是一个非常简单的问题,但是很多人没有接触过,所以就认为很难,面试的时候当然就写不出来了,今天我们就重点通关层次遍历这个问题。
1. 层次遍历介绍
广度优先在面试中属于常考类型,整体来说属于简单次,但是很多人面试遇到了就放弃,真的很可惜。我们就看看它的难度在哪里。
广度优先又叫做层次遍历,基本过程如下:
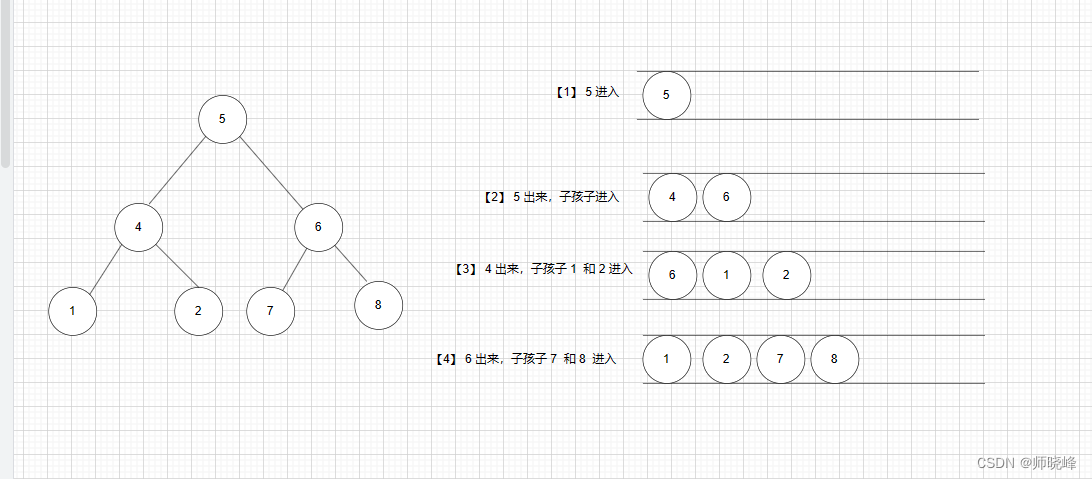
层次遍历就是从根节点开始,先访问根节点的一层全部元素,在访问之后的一层,类似金字塔一样一层一层访问。我们可以看做就是从左到右的一层一层去遍历二叉树,先访问5,之后访问3的左右孩子4 和 6 ,之后再访问4 和 6的孩子1 2 和 7 8。最后得到结果【5,4,6,1,2,7,8】
这里的问题就变成了将遍历过的子孩子保存下来,比如访问4 的左右孩子1 和 2 的时候应该先存储,直到处理完20之后再处理。使用队列的话就可以解决上述问题。
看下过程图解:
- 根节点入队 5
- 然后 5 出队, 之后将 5 的左右孩子4 6入队,保存在队列中
- 4 出队,将4 的左右孩子 1 2 入队
- 之后 6 出队,将 6 的左右孩子 7 8 入队,保存在队列中
- 最终 1 2 7 8 依次出队,此时都是叶子几点,只要出队就行了。
这个过程不复杂,如果将树的每层分开,是不是可以整活😎了?首先,能否将每层的元素顺序反转一下?或者说奇数不变,偶数反转?是否将输出层次从低到高(root)输出呢?再比如,既然可以拿到每层的元素,能不能找到当前层最大的元素?最小的元素呢?最右端的元素(右视图)?最左端的元素(左视图)?整个层的平均值?当然这都是可以实现的嘞😋,这么来回折腾有啥用呢?🤔,没啥用了,但是这些都是层次遍历的高频算法题目。
推荐力扣题目⭐⭐⭐⭐:
102. 二叉树的层序遍历 - 力扣(LeetCode)
107. 二叉树的层序遍历 II - 力扣(LeetCode)
199. 二叉树的右视图 - 力扣(LeetCode)
637. 二叉树的层平均值 - 力扣(LeetCode)
429. N 叉树的层序遍历 - 力扣(LeetCode)
515. 在每个树行中找最大值 - 力扣(LeetCode)
116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode)
117. 填充每个节点的下一个右侧节点指针 II - 力扣(LeetCode)
103. 二叉树的锯齿形层序遍历 - 力扣(LeetCode)
2. 基本的层次遍历与变换
我们看一个最简单的情况,仅仅是遍历并输出全部元素,如下图:

上图的输入结果【5,4,6,7,8】,方法已经梳理过了,这里看一下代码怎么实现。先访问根节点,然后其左右孩子入队,接着出队,出队的元素将其左右孩子入队,直到队列为空就可以退出了:
/**
* 二叉树层序遍历
* @param root
* @return
*/
public static List<Integer> simpleLevelOrder(TreeNode root) {
// 参数校验
if (root == null) {
return new ArrayList<Integer>();
}
// 创建存储空间
List<Integer> res = new ArrayList<Integer>();
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点先入队
queue.add(root);
// 遍历队列元素
while(queue.size() > 0){
// 获取当前队列的长度,这个长度相当于这一层的节点个数
TreeNode t = queue.remove();
res.add(t.val);
if (t.left != null){
queue.add(t.left);
}
if (t.right != null){
queue.add(t.right);
}
}
return res;
}
注意:
根据树的结构可以看出,一个节点在一层访问之后,其子孩子都是在下层按照FIFO的顺序处理的,因此队列在这里起到了一个缓存的作用。
如果要你将每层的元素分开该怎么做呢?看下下面的这个题:
2.1 二叉树的层次遍历
题目介绍:102. 二叉树的层序遍历 - 力扣(LeetCode)
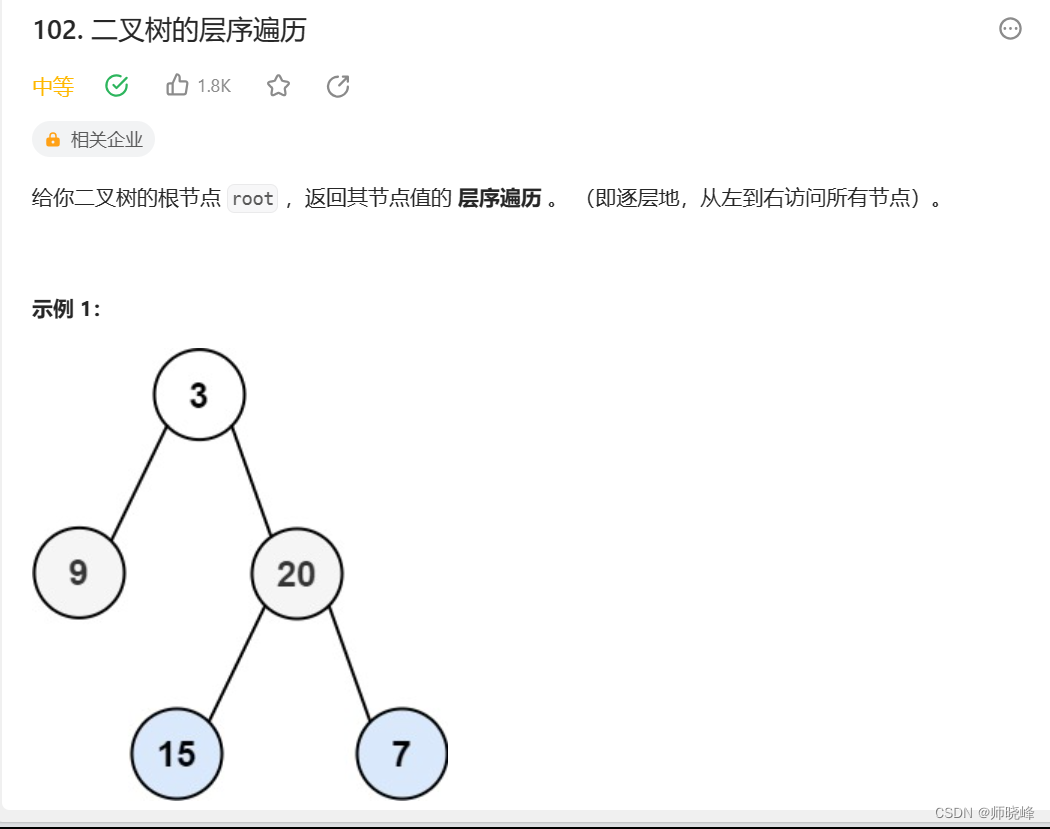

我们再来看这个执行过程,我们先将根节点放入队列中,然后不断的遍历队列。

那如何判断某一层访问完了呢?这个简单,我们用一个size标记一下就行了,size表示某一层元素的个数,知道出队,size就减1,减到0就说明该层访问完了,当size变成0之后,这时队列中甚于元素个数恰好就是下一次的个数,因此重新将size标记为下一层的元素个数就可以继续处理新的一行,例如上面的序列中:
- 首先获取根节点 3 ,左右子节点不为空,将左右子节点放入队列,此时3 已经出队。剩下的9 20 恰好是第二层的所有节点,此时size = 2
- 继续将9 出队,左右节点不为空,将左右节点放入队列,size-- ,变成 1 ,之后将20 出队,左右节点不为空,将左右节点放入队列 size–, 变为 0。当size = 0,说明当前层已经处理完了,此时队列有4个元素,恰好是下一层的元素个数。
- 最后,我们把每层遍历到的节点放入一个结果集中,将其返回就可以了
按层次遍历经典代码:
/**
* 层次遍历 经典方式
* @param root
* @return
*/
public static List<List<Integer>> level102Order(TreeNode root) {
// 校验参数
if (root == null){
return new ArrayList<List<Integer>>();
}
// 创建空间
List<List<Integer>> res = new ArrayList<List<Integer>>();
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
// 将根节点放入队列 然后不断遍历队列
queue.add(root);
while(queue.size() > 0){
// 获取当前size的个数 即当前层有多少个元素
int size = queue.size();
// 创建临时空间 将一层的元素存入其中
List<Integer> temp = new ArrayList<Integer>();
for(int i = 0; i < size; i++){
TreeNode t = queue.remove();
temp.add(t.val);
if (t.left != null){
queue.add(t.left);
}
if (t.right != null){
queue.add(t.right);
}
}
// 此时的temp就是一层的所有元素,用list类型保存temp,最后加入到结果集中
res.add(temp);
}
return res;
}
此方法一定要牢记,在算法体系中是很重要的一环,他与链表反转,二分查找可以相提并论,务必掌握,彻底理解,然后记忆。
当然上面的算法理解了,下面的一系列题目都变得简单了,不信你往下看。
注意:
在Java中队列的实现不止一种,需要注意。
2.2 层次遍历-自底向上
题目介绍:107. 二叉树的层序遍历 II - 力扣(LeetCode)


如果要求从上到下输出每一层的节点值,做法很直观,在遍历完一层之后,将该层存储节点值的列表添加到结果集的尾部。这道题要求从下到上输出每一层的节点值,只要对上述操作稍作修改就可以了,在遍历完一层节点后,将存储该层节点值的列表添加到结果集的头部。
为了降低在结果列表的头部添加一层节点值的列表的时间复杂度,结果列表可以使用链表的结构,在链表头部添加一层节点值的列表的时间复杂度为O(1),在Java中,由于我们需要返回一个List接口,在这里可以使用链表实现。
代码就很普通了😎:
/**
* 层序遍历 自底向上
* @param root
* @return
*/
public static List<List<Integer>> levelOrderBottom(TreeNode root) {
// 校验参数
if (root == null){
return new ArrayList<List<Integer>>();
}
// 创建空间
List<List<Integer>> levelOrder = new LinkedList<List<Integer>>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点存入队列中 不断的遍历
queue.offer(root);
while(queue.size() > 0){
List<Integer> level = new ArrayList<Integer>();
int size = queue.size();
for(int i = 0; i < size; i++){
TreeNode node = queue.poll();
level.add(node.val);
// 这样也行
TreeNode left = node.left,right = node.right;
if(left != null){
queue.offer(left);
}
if (right != null){
queue.offer(right);
}
}
levelOrder.add(0,level); // 放在头部 栈
}
return levelOrder;
}
2.3 二叉树的锯齿形层次遍历
题目介绍:103. 二叉树的锯齿形层序遍历 - 力扣(LeetCode)
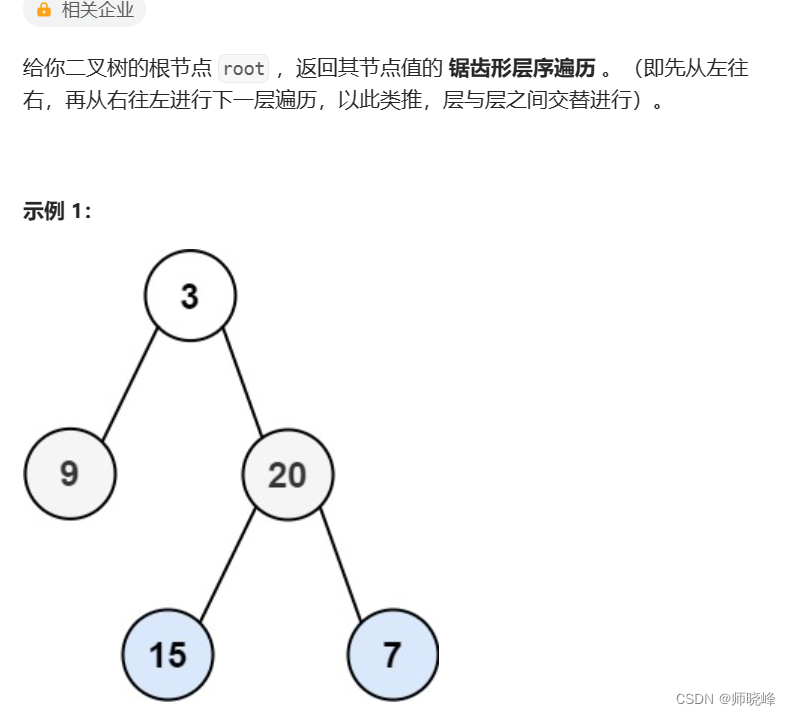

这个题也是102. 二叉树的层序遍历 - 力扣(LeetCode)的变种,只是最后输出的要求变化了,要求我们按照层数的奇偶来决定每层输出的顺序,如果当前是偶数层,从左到右输出当前层的节点值,否则,从右至左输出当前层的节点值。这里我们同样可以采用102的方法思想。
但是为了满足条件,【左右->右左】交替暑促的锯齿形,可以利用【双端队列】的数据机构来维护当前节点值的输出顺序。双端队列是一个可以在队列任意一端插入元素的队列。在广度优先遍历搜索当前节点,扩展下一层节点的时候我们仍然可以从左往右循序扩展,但是对于当前层节点的存储我们维护一个变量isOrderLeft记录时从左到右还是从右到左:
- 如果从左到右,我们每次将被遍历的元素插入到双端队列的末尾
- 从右到左,我们每次将被遍历的元素插入到双端队列的头部。
代码展示😋
/**
* 锯齿层次遍历
* @param root
* @return
*/
public static List<List<Integer>> zigzagLevelOrder(TreeNode root) {
// 校验参数
if (root == null){
return new ArrayList<List<Integer>>();
}
// 创建空间
List<List<Integer>> ans = new LinkedList<List<Integer>>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 将根节点放入队列 不断循环遍历
queue.offer(root);
// 判断奇偶变量
boolean isOrderLeft = true;
while(queue.size() >0){
// 这里要使用双端队列
Deque<Integer> temp = new LinkedList<Integer>();
int size = queue.size();
for(int i = 0; i < size; i++){
TreeNode t = queue.poll();
if (isOrderLeft){
temp.offerLast(t.val);
}else{
temp.offerFirst(t.val);
}
if (t.left != null){
queue.offer(t.left);
}
if (t.right != null){
queue.offer(t.right);
}
}
ans.add(new LinkedList<Integer>(temp));
isOrderLeft = !isOrderLeft;
}
return ans;
}
2.4 N叉树的层次遍历
题目介绍:429. N 叉树的层序遍历 - 力扣(LeetCode)


首先看下N叉树的结构,就是一个值的不同,变成了以一个列表,其类型仍然时Node:
class TreeNode {
public int val;
public List<TreeNode> children;
}
也就是说我们可以说,这个也是102. 二叉树的层序遍历 - 力扣(LeetCode)的变种,我们就用简单的广度优先,借助队列即可实现。
/**
* N 叉树的遍历
* @param root
* @return
*/
public static List<List<Integer>> nLevelOrder(NTreeNode root) {
// 校验参数
if (root == null){
return new ArrayList<List<Integer>>();
}
// 创建空间
List<List<Integer>> res = new ArrayList<List<Integer>>();
Deque<NTreeNode> queue = new ArrayDeque<NTreeNode>();
// 根节点放入队列 不断遍历
queue.offer(root);
while(!queue.isEmpty()){
Deque<NTreeNode> next = new ArrayDeque<>();
List<Integer> level = new ArrayList<>();
while(!queue.isEmpty()){
NTreeNode current = queue.pollFirst();
level.add(current.val);
// 注意这里链表遍历
for (NTreeNode child : current.children){
if (child != null){
next.add(child);
}
}
}
// 重新定义queue
queue = next;
res.add(level);
}
return res;
}
3. 几个处理每层元素的题目
如果我们拿到每一层的元素,那么是不是可以利用一下就可以造几个题目出来呢?例如每层找最大的值,平均值,最右侧的值?当然可以。这也是力扣的上面比较经典的题目了:
题目推荐⭐⭐⭐⭐:
515. 在每个树行中找最大值 - 力扣(LeetCode)
637. 二叉树的层平均值 - 力扣(LeetCode)
199. 二叉树的右视图 - 力扣(LeetCode)
当然我们自己也可以造题目,比如说层次取最小值可以吗?每层的最左侧值可以不?是不是现在发现算法其实很好玩的🥰
3.1 在每棵树行中找出最大值
题目介绍:515. 在每个树行中找最大值 - 力扣(LeetCode)

这里其实就是得到一层之后使用一个变量来记录当前的最大值:
代码也很简单:
/**
* 层序遍历找到每层最大值
* @param root
* @return
*/
public static List<Integer> largestValues(TreeNode root) {
// 校验参数
if(root == null){
return new ArrayList<Integer>();
}
// 创建空间
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> queue = new ArrayDeque<TreeNode>();
// 根节点入队,不断循环遍历
queue.offer(root);
while(queue.size() > 0){
int size = queue.size();
int maxLevel = Integer.MIN_VALUE;
for(int i = 0; i < size; i++){
TreeNode t = queue.poll();
maxLevel = Math.max(maxLevel, t.val);
if (t.left != null){
queue.offer(t.left);
}
if (t.right != null){
queue.offer(t.right);
}
}
res.add(maxLevel);
}
return res;
}
3.2 在每棵树行中找出平均值
题目介绍:637. 二叉树的层平均值 - 力扣(LeetCode)
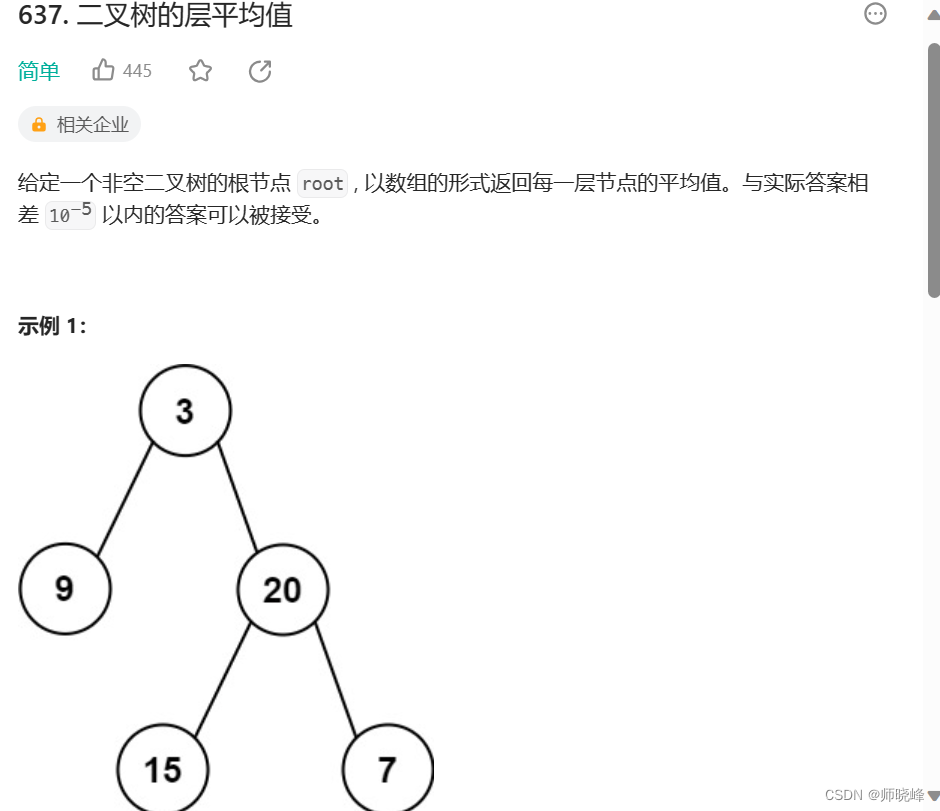
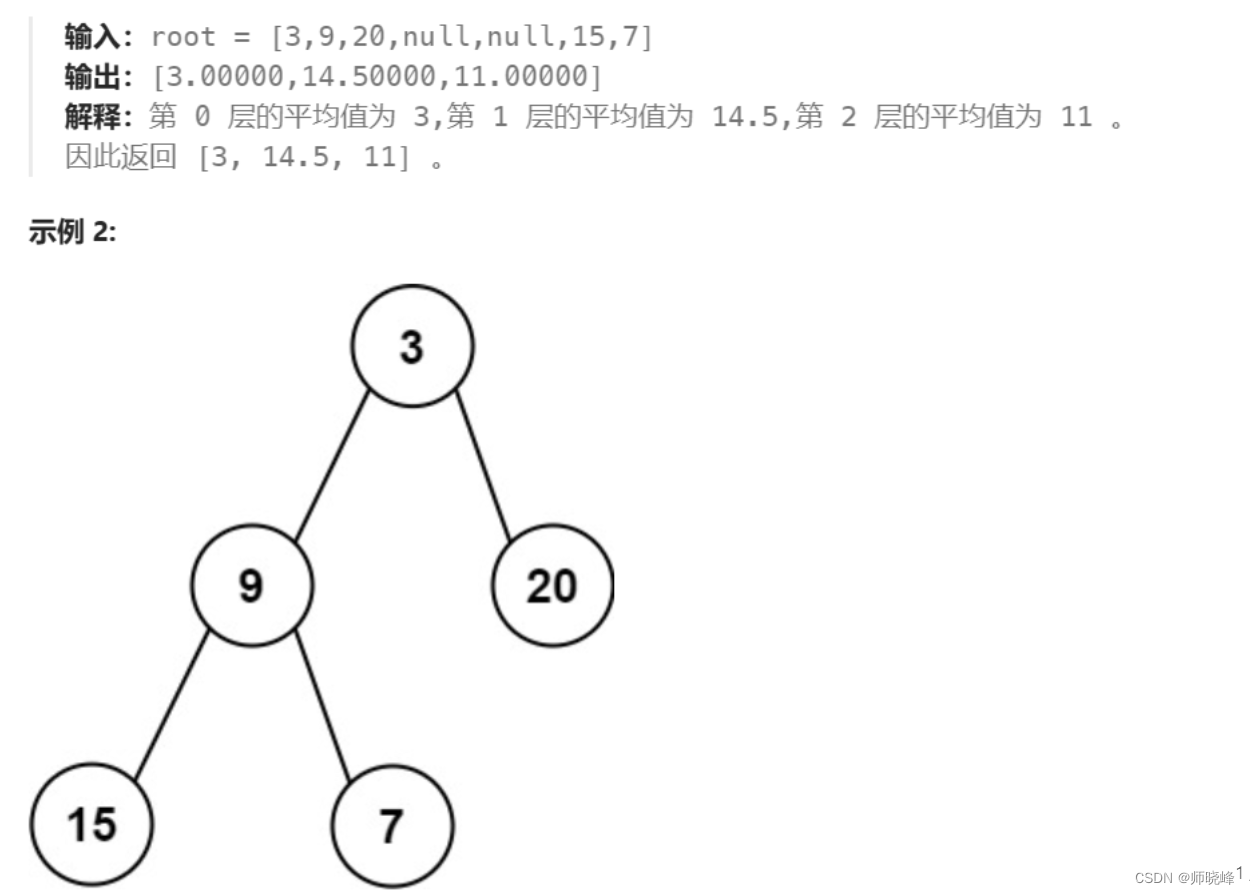
这个题目和前面的一样,之不多每层都先将元素保存下来,最后求一个平均值就可以了,是不是是很简单;
/**
* 层序遍历,求出每层平均值
* @param root
* @return
*/
public static List<Double> averageOfLevels(TreeNode root) {
// 检验参数
if(root == null){
return new ArrayList<Double>();
}
// 创建空间
List<Double> res = new ArrayList<Double>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点入队,不断循环
queue.offer(root);
while(queue.size() > 0){
int size = queue.size();
double sum = 0;
for(int i = 0; i < size; i++ ){
TreeNode t = queue.poll();
sum += t.val;
if (t.left != null){
queue.offer(t.left);
}
if (t.right != null){
queue.offer(t.right);
}
}
res.add(sum/size);
}
return res;
}
3.3 二叉树的右视图
题目介绍:199. 二叉树的右视图 - 力扣(LeetCode)


这个题目说实话出频率还挺高的,如果没有提前思考过,很难想到答案。其实也简单,在BFS进行层次遍历的时候,记录下每层的最后一个元素就可以了。
/**
* 层序遍历,输出右视图
* @param root
* @return
*/
public static List<Integer> rightSideView(TreeNode root) {
// 校验参数
if(root == null){
return new ArrayList<Integer>();
}
// 创建空间
List<Integer> res = new ArrayList<Integer>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点入队,不断循环遍历
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
TreeNode t = queue.poll();
if (t.left != null){
queue.offer(t.left);
}
if (t.right != null){
queue.offer(t.right);
}
// 这里将最后一个节点放入结果集中
if (i == size - 1){
res.add(t.val);
}
}
}
return res;
}
是不是有点成就感了,感觉算法是有套路的,并不是四刷题目。这三道题基本上都是层序遍历的变种。
那我我们也可以尝试着造出题目来:
有右视图,那么左视图行不行?俯视图行不行?想一下💡
嘿嘿😁,我这里告诉你吧,俯视图不行,但是左视图可以,想下为什么?🤔
3.4 最底层最左边
题目介绍:513. 找树左下角的值 - 力扣(LeetCode)

在第二部分,我们写了很多层次遍历的变种形式,这里有两个问题:
- 该怎么知道什么时候到最底层了?
- 加入最底层有两个,该怎么知道那个时最左的呢?
带着这两个问题,我们再看下层序遍历的执行过程:
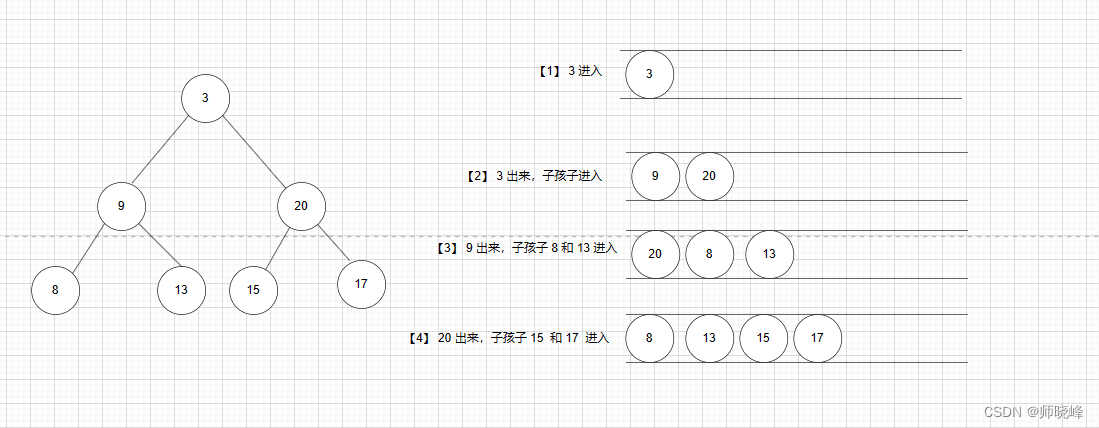
我们可以发现,正常执行层次遍历的,不管最底层有几个元素,最后输出的一定是底层最右的元素7,这里我们就想象一下,可不可以和上面题目一样结合反转操作实现呢,每一层先反转再存入队列,到最后是不是输出的为最左节点值呢?是的,知道了这个解题关键点,我想答案你已经会写了🥰。
public int findBottomLeftValue(TreeNode root) {
// 校验参数
if(root.left == null && root.right == null){
return root.val;
}
// 创建空间
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点入队,不断循环遍历
queue.offer(root);
TreeNode temp = new TreeNode();
while(!queue.isEmpty()){
temp = queue.poll();
// 先右后左
if(temp.right != null){
queue.offer(temp.right);
}
if(temp.left != null){
queue.offer(temp.left);
}
}
return temp.val;
}
总结
提示:二叉树的层序遍历,各种变种问题,熟练掌握模板题,总结套路,是不是感觉算法也是有迹可循的😎