1.算法思想

折半查找，又称“二分查找”，仅适用于有序的顺序表。

1.适用范围

顺序表拥有随机访问的特性，链表没有。

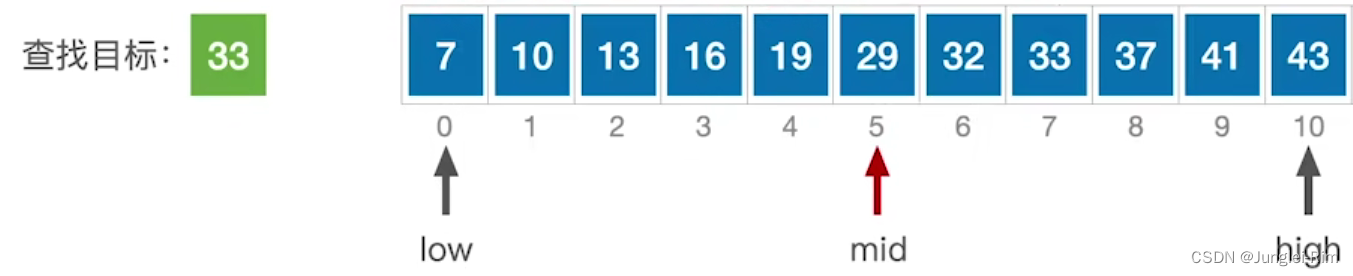
图解：（low代表左区间边界，high代表右区间边界，mid代表中间元素）

2.算法实现

实现步骤：

1. 将元素进行排序
2. 定义两个变量left,right分别遍历中间元素mid的左右区间
3. 每一轮循环，分别与中间元素比较大小，确定目标元素的区间
4. 若目标元素在mid的左边，则让left = mid-1;
5. 若目标元素在mid的右边，则让right = mid+1;
6. 并且每一轮循环，让mid = （right+left）/2；
7. 循环结束条件：若查找成功则left = right,返回mid；若left > rigth则查找失败，返回-1.

代码实现：

typedef struct {//查找表的数据结构（顺序表)
    ElemType *elem;//动态数组基址
    int TableLen;//表的长度
} SSTable;

//折半查找
int Binary_Search(SSTable L, ElemType key) {
    int low = 0, high = L.TableLen - 1, mid;
    while (low <= high) {
        mid = (low + high) / 2;//取中间位置
        if (L.elem[mid] == key)
            return mid;//查找成功则返回所在位置
        else if (L.elem[mid] > key)
            high = mid - 1;//从前半部分继续查找
        else
            low = mid + 1;//从后半部分继续查找
    }
    return -1; //查找失败，返回-1
}

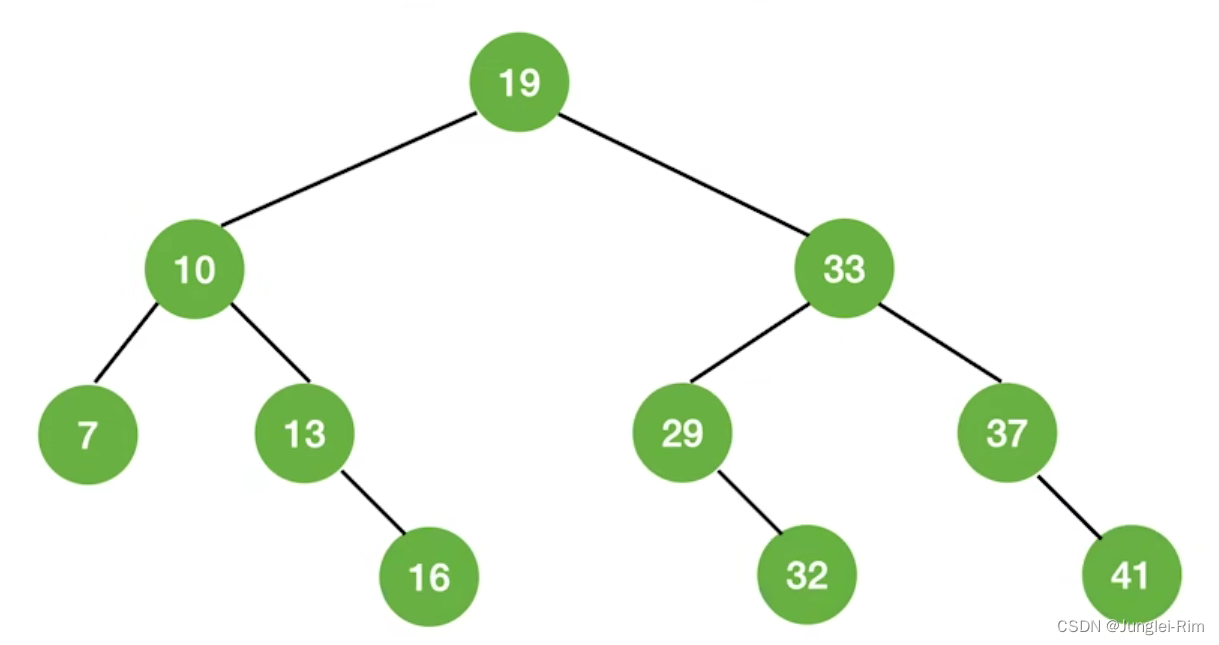
3.查找判定树

1.构造方法

• 由mid所指元素将原有元素分割到左右子树中。
• Key:右子树结点数–左子树结点树=0或1。
• 折半元素的计算方法：mid = [(low + high)/2]（向下取整）；

1.折半查找判定树的特点

• 如果当前low和high之间有奇数个元素，则mid分隔后，左右两部分元素个数相等。
• 如果当前low和high之间有偶数个元素，则mid分隔后，左半部分比右半部分少一个元素。
• 折半查找的判定树中，则对于任何一个结点，必有右子树结点数-左子树结点数=0或1。
• 由于折半查找的判定树的任意左右子树的结点数不大于1，则该判定树一定是平衡二叉树。

2.折半查找判定树的相关计算

• 折半查找的判定树中，只有最下面一层是不满的，因此元素个数为n时树高:$$h=lo{g}_2(n+1)$$
• 判定树结点关键字:左<中<右，满足二叉排序树的定义,失败结点:n+1个（等于成功结点的空链域数量)

4.折半查找效率

1.折半查找时的ASL的计算

在不考虑失败的情况下，折半查找的树高为：$$lo{g}_2(n+1)$$

也就是说查找成功的ASL(平均查找长度)<=h,同样查找失败的ASL也不会超过h+1.

2.时间复杂度

所以可以得出结论：折半查找的时间复杂度应该是：$$O(lo{g}_{2}n)$$这个数量级。