OpenCV（三十七）：拟合直线、三角形和圆形

news2024/11/20 9:30:00

1.点集拟合的含义

点集拟合是一种通过拟合函数或曲线来近似描述给定离散数据点的技术,在点集拟合中，可以使用不同的函数或曲线拟合方法来拟合直线、三角形和圆形。

直线拟合：对于给定的二维数据点集合，可以使用最小二乘法来拟合一条直线。

三角形拟合：对于给定的二维或三维数据点集合，可以使用三角形拟合方法来找到尽可能逼近数据点的最佳三角形。

圆形拟合：对于给定的二维数据点集合，可以使用圆形拟合方法来找到与数据点分布最佳匹配的圆。

2.拟合直线的函数fitLine()

void cv::fitLine ( InputArray points,

OutputArray line,

int distType,

double param,

double reps,

double aeps

)

points:输入待拟合直线的2D或者3D点集。
line:输出描述直线的参数，2D点集描述参数为Vec4f类型，3D点集描述参数为Vec6f类型distType:M-estimator算法使用的距离类型标志。
param:某些类型距离的数值参数(C)。如果数值为0，则自动选择最佳值。
reps: 坐标原点与直线之间的距离精度，数值0表示选择自适应参数，一般常选择0.01
aeps:直线角度精度，数值0表示选择自适应参数，一般常选择0.01。

距离类型选择标志

示例代码：

 //直线拟合
    Vec4f lines;//存放拟合后的直线
    vector<Point2f> point;//待检测是否存在直线的所有点
    const static float Points[20][2]={
            {0.0f,0.0f},{10.0f,11.0f},{21.0f,20.0f},{30.0f,30.0f},
            {40.0f,42.0f},{50.0f,50.0f},{60.0f,60.0f},{70.0f,70.0f},
            {80.0f,80.0f},{90.0f,92.0f},{100.0f,100.0f},{110.0f,110.0f},
            {120.0f,120.0f},{136.0f,130.0f},{138.0f,140.0f},{150.0f,150.0f},
            {160.0f,163.0f},{175.0f,170.0f},{181.0f,180.0f},{200.0f,190.0f},
    };
    //将所有点存放在vector中，用于输入函数中
    for(int i=0;i<20;i++){
        point.push_back(Point2f(Points[i][0],Points[i][1]));
    }
    //参数设置
    double param=0;//距离模型中的数值参数C
    double reps=0.01;//坐标原点与直线之间的距离精度
    double aeps=0.01;//角度精度
    fitLine(point,lines,DIST_L1,0,0.01,0.01);
    double k=lines[1]/lines[0];//直线斜率
    ostringstream ss;
    ss<<"直线效率："<<k<<endl;
    ss<<"直线上一点坐标x："<<lines[2]<<",y:"<<lines[3]<<endl;
    ss<<"直线解析式：y="<<k<<"(x-"<<lines[2]<<")+"<<lines[3]<<endl;
    LOGD("%s",ss.str().c_str());

运行结果：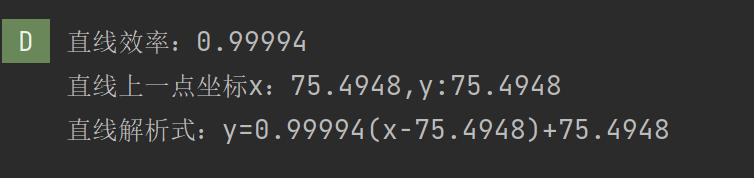

3.拟合三角形的函数 minEnclosingTriangle()

double cv::minEnclosingTriangle ( InputArray points,OutputArray triangle）

points:待寻找包围三角形的2D点集
triangle:拟合出的三角形三个顶点坐标

4.拟合三角形的函数 minEnclosingTriangle()

minEnclosingCircle()

void cv::minEnclosingCircle ( InputArray points,

Point2f &center，

float &radius

）

points:待寻找包围圆形的2D点集
center:圆形的圆心。
radius:圆形的半径

拟合三角形和圆形的示例代码：

//点集拟合
void Point_set_fitting(){
  
    Mat img(500,500,CV_8UC3,Scalar::all(0));
    RNG &rng=theRNG();

    int i,count=rng.uniform(1,101);
    vector<Point> points;
    //生成随机点
    for(i=0;i<count;i++){
            Point  pt;
            pt.x=rng.uniform(img.cols/4,img.cols*3/4);
            pt.y=rng.uniform(img.rows/4,img.rows*3/4);
            points.push_back(pt);
    }
    //寻找包围点集的三角形
    vector<Point2f> triangle;
    double area= minEnclosingTriangle(points,triangle);
    //寻找包围点集的圆形
    Point2f center;
    float radius=0;
    minEnclosingCircle(points,center,radius);

    //创建两个图片用于输出结果
    img=Scalar ::all(0);
    Mat img2;
    img.copyTo(img2);
    //在图像中绘制坐标点
    for(i=0;i<count;i++){
        circle(img,points[i],3,Scalar(255,255,255),FILLED,LINE_AA);
        circle(img2,points[i],3,Scalar(255,255,255),FILLED,LINE_AA);
    }
    //绘制三角形
    for(i=0;i<3;i++){
        if(i==2){
            line(img,triangle[i],triangle[0],Scalar(255,255,255),1,16);
            break;
        }
        line(img,triangle[i],triangle[i+1],Scalar(255,255,255),1,16);
    }
    //绘制圆形
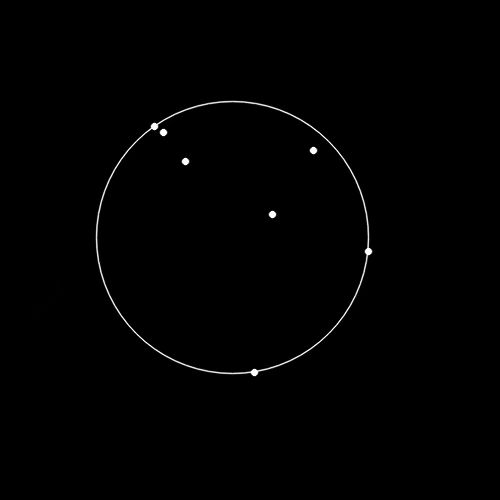
    circle(img2,center, cvRound(radius),Scalar(255,255,255),1,LINE_AA);

    //显示图像
    imwrite("/sdcard/DCIM/img.png",img);
    imwrite("/sdcard/DCIM/img2.png",img2);

}

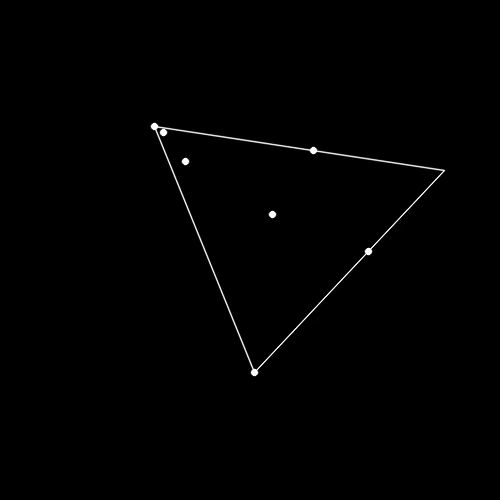
三角形拟合的结果：