NTC 温度采样：
本文记录对NTC 温度采样，分别采用二分查表法及公式法进行描述
资源下载链接：Excel 生成数组表 https://download.csdn.net/download/qq_41359157/88326839?spm=1001.2014.3001.5503
NTC参数：
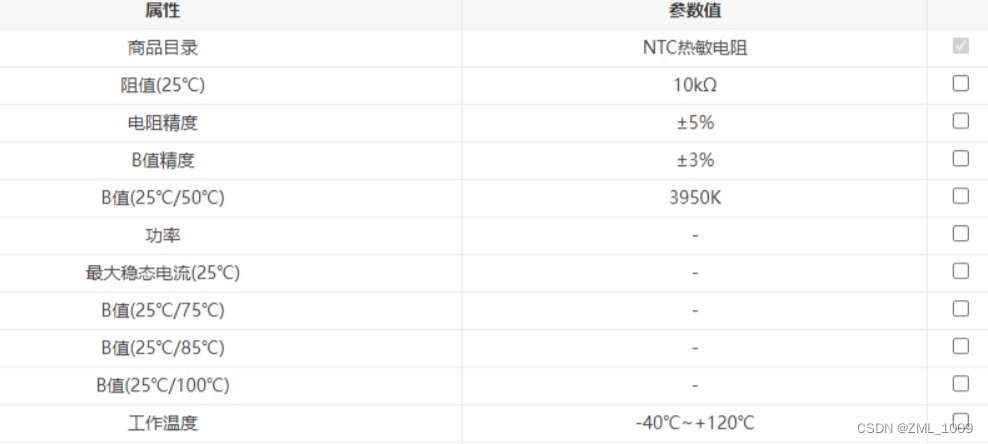
NTC采样电路：
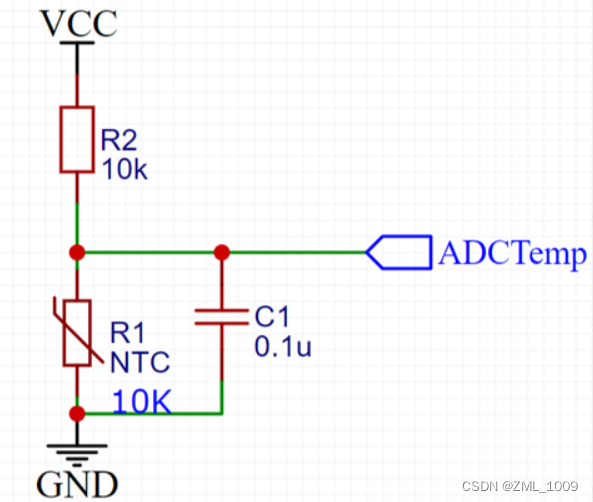
一、 二分查表法：
二分法，二分查找很高效，假设数据大小是n，每次查找后数据都会缩小为原来的一半，也就是会除以2。二分法查找针对的是一个有序的数据集合（升序或降序排列）。
（1）首先，从数组的中间元素开始搜索，如果该元素正好是目标元素，则搜索过程结束，否则执行下一步。
（2）如果目标元素大于/小于中间元素，则在数组大于/小于中间元素的那一半区域查找，然后重复步骤（1）的操作。
比如，我们需要查找4。
- 先取一半为6， 6 大于 4。则说明要找的数在前一半，此时end需要挪到mid-1处
- 再取一半为3， 3 小于 4。则说明要找的数在后一半，此时start需要挪到mid+1处
- 再次查找，则可以找到目标值。当然对于温度来讲，只知道一个范围区间，这个下面再讲
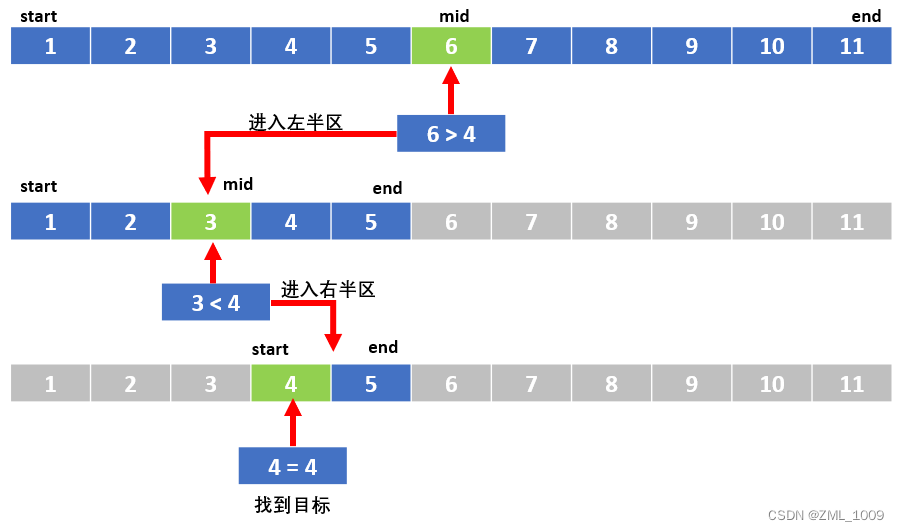因为NTC的AD值正好是表中的值概率很小，很可能查不到，但是我们可以知道落在了哪个区间，所以要处理的数据基本上在两个温度的区间，如果要显示小数，两个温度区间可以看成是线性的，通过局部线性化就可以计算出温度的值。
假设ADC采样的值是2075，则对应在数据表中的2093~2048之间，及在24 ℃ ~ 25 ℃之间
计算方式按照线性处理如下:
代码部分：
头文件部分：这里我生成了两个表格，一个是ADC的表格，一个是与其对应的温度表格
static const uint16 NTC_adc_table[] =
{
3996, 3988, 3981, 3972, 3964, 3955, 3945, 3935, 3924, 3912,
3900, 3887, 3874, 3860, 3845, 3830, 3813, 3796, 3778, 3760,
3740, 3720, 3698, 3676, 3653, 3629, 3604, 3578, 3551, 3524,
3495, 3465, 3435, 3403, 3371, 3337, 3303, 3267, 3231, 3194,
3156, 3118, 3078, 3038, 2997, 2955, 2913, 2870, 2826, 2782,
2738, 2693, 2648, 2602, 2556, 2510, 2464, 2417, 2371, 2324,
2278, 2231, 2185, 2139, 2093, 2048, 2002, 1957, 1913, 1868,
1825, 1781, 1739, 1697, 1655, 1614, 1574, 1534, 1495, 1456,
1419, 1382, 1346, 1310, 1275, 1241, 1208, 1175, 1143, 1112,
1081, 1052, 1023, 994, 967, 940, 914, 888, 863, 839,
815, 792, 770, 748, 727, 707, 687, 668, 649, 631,
613, 596, 579, 563, 547, 532, 517, 502, 488, 475,
462, 449, 436, 424, 413, 401, 390, 380, 369, 359,
350, 340, 331, 322, 314, 305, 297, 289, 282, 274,
267, 260, 253, 247, 240, 234, 228, 222, 217, 211,
206, 201, 196, 191, 186, 181, 177, 173, 168, 164,
160
};
static const sint16 NTC_temperature_table[] =
{
-40, -39, -38, -37, -36, -35, -34, -33, -32, -31,
-30, -29, -28, -27, -26, -25, -24, -23, -22, -21,
-20, -19, -18, -17, -16, -15, -14, -13, -12, -11,
-10, -9, -8, -7, -6, -5, -4, -3, -2, -1,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47, 48, 49,
50, 51, 52, 53, 54, 55, 56, 57, 58, 59,
60, 61, 62, 63, 64, 65, 66, 67, 68, 69,
70, 71, 72, 73, 74, 75, 76, 77, 78, 79,
80, 81, 82, 83, 84, 85, 86, 87, 88, 89,
90, 91, 92, 93, 94, 95, 96, 97, 98, 99,
100, 101, 102, 103, 104, 105, 106, 107, 108, 109,
110, 111, 112, 113, 114, 115, 116, 117, 118, 119,
120
};
源文件部分：
#define TSP_SHORT_CIRCUIT_THRESHOLD 20U /*!<NTC short-circuit */
#define TSP_OPEN_CIRCUIT_THRESHOLD 4090U /*!<NTC open-circuit */
/*------------------------------------------------------------------------------*/
/*!
* \brief tsp_BinaryTableSearch
* \details Calculation of NTC temperature by binary table lookup method
* \param[in] adc_val current adc value
* \param[out] float32 Temperature( degree centigrade )
*/
/*------------------------------------------------------------------------------*/
static float32 tsp_BinaryTableSearch( uint16 adc_val )
{
uint16 start = 0U, end = 0U, mid = 0U;
/* Get the arry length */
end = ( sizeof( NTC_adc_table )/ sizeof( NTC_adc_table[0] ) ) - 1U;
/* Data anomaly judgment */
if( adc_val <= TSP_SHORT_CIRCUIT_THRESHOLD )
{
return 1.0F;
}
else if( adc_val >= TSP_OPEN_CIRCUIT_THRESHOLD )
{
return 2.0F;
}
else if( adc_val > NTC_adc_table[0] )
{
return 3.0F;
}
else if( adc_val < NTC_adc_table[end - 1U] )
{
return 4.0F;
}
else
{
/* MISRA-C coding rules */
}
while ( start <= end )
{
/* Get the mid value */
mid = (start + end) >> 1;
/* Just find */
if( adc_val == NTC_adc_table[mid] )
{
break;
}
/* Right in between two temperature points */
if( ( adc_val < NTC_adc_table[mid] ) && ( adc_val > NTC_adc_table[mid+1U] ) )
{
break;
}
/* The current AD value less than the middle of the array indicates
* the second half of the number to look for
*/
if( adc_val < NTC_adc_table[mid] )
{
start = mid + 1U;
}
/* The current AD value greater than the middle of the array indicates
* that the number to be found is in the first half
*/
else if( adc_val > NTC_adc_table[mid] )
{
end = mid - 1U;
}
else
{
/* MISRA-C coding rules */
}
}
return ( NTC_temperature_table[mid] + (float)( NTC_adc_table[mid] - adc_val ) / (float)( NTC_adc_table[mid]-NTC_adc_table[mid+1] ) );
// return (mid-40) + (float)(NTC_adc_table[mid] -key)/(float)(NTC_adc_table[mid]-NTC_adc_table[mid+1]);
}
这里我们可以采用两种方法，一种是通过ADC的值索引到当前表中的位置，再根据这个mid位置索引到温度表格中的值，然后进行计算。
还有一种就是注释的部分：
return (mid-40) + (float)(NTC_adc_table[mid] -key)/(float)(NTC_adc_table[mid]-NTC_adc_table[mid+1]);
这里的mid - 40代表的是，这个表格前面有40个负值温度，通过mid-40 可以得到当前温度的整数部分。这种方法比较固定，写程序时得确定当前温度范围值。
如果采用第二种方法，只需要配置参数，生成头文件即可。
excel表格配置：
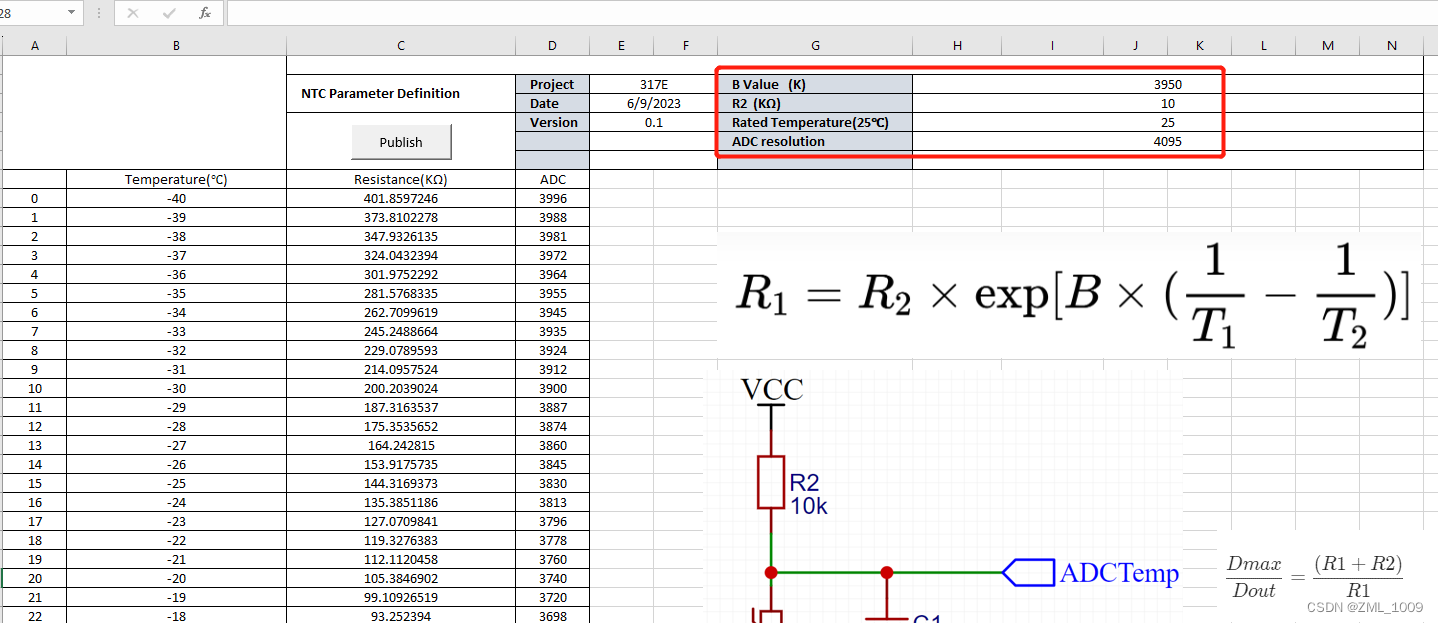
只需要填写相关属性参数，点击Publish即可生成头文件
二、 公式法 —— 温度系数B值计算法：
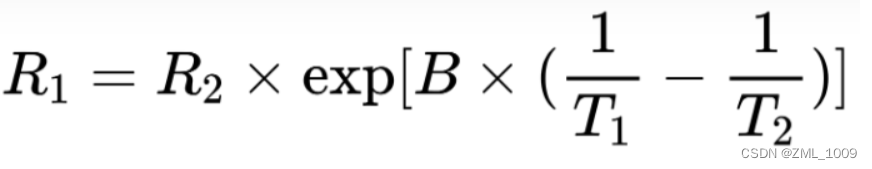
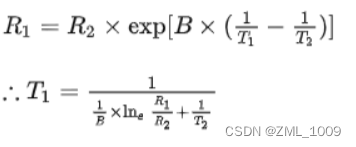
这里T1和T2指的是K度即开尔文温度
| X | |
|---|---|
| R1 | NTC在T(K)温度下的阻值, T1温度下的阻值 |
| R2 | NTC在25℃下的阻值（10K、5K、100K…）即：在额定温度 TN （ K ）时的 NTC 热敏电阻阻值,T2常温下的标称阻值。 |
| B | NTC 热敏电阻的材料常数，又叫热敏指数 (3435，3950…) |
| T1 | NTC的温度 |
| T2 | 273.15+25 (开尔文基数 + 额定阻值下的温度) |
通过转换可以得到温度T1与电阻Rt的关系:
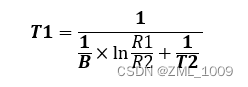
因为C语言的math.h中没有ln表达，有log可以进行替代，
这里可以将ln换算成log:
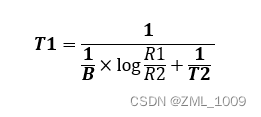
其他博客统一写上了：
对应的摄氏温度t=T1-273.15，同时+0.5的误差矫正。
本人通过跟查表法对比，发现加了0.5误差矫正反而就多了0.5，所以实际程序中不添加0.5进行误差矫正。
代码部分：
#ifdef NTC_SUPPORT
#include <math.h>
#define TSP_NTC_B_VALUE 3950U /*!<NTC B value */
#define TSP_NTC_RATED_TEMP 25U /*!<NTC rated temperature(25℃) */
#define TSP_NTC_RATED_RES 10000.0F /*!<NTC rated resistance 10K*/
#define TSP_NTC_KELVIN_VALUE 273.15F /*!<NTC kelvin value */
#define TSP_NTC_T2_VALUE TSP_NTC_KELVIN_VALUE + TSP_NTC_RATED_TEMP
#define TSP_NTC_ERROR_VALUE 0.5F /*!<NTC error,log replace of ln, need to add the error */
#define TSP_ADC_FULL_SCALE 4095.0F /*!<ADC scale*/
#define TSP_ADC_VOLTAGE_REF 3.3F /*!<Voltage reference*/
/*
* Temperature Configuration Data:
* TSP_HOT_TEMP_LIMIT
* TSP_COLD_TEMP_LIMIT
* TSP_MAX_SAMPLE_NUM
* TSP_NTC_B_VALUE
* TSP_NTC_RATED_TEMP
* TSP_NTC_RATED_RES
* Temperature Conversion Equations:
* T[Volt] = T[ADC] * (3.3 / 1023)
* T[degree] = ( 1 / ( ln(Rt/Rp) / B + 1/T2 ) ) - 273.15
*/
double tsp_ln(double a)
{
int N = 15;
int k , nk;
double x, xx , y;
x = ( a - 1 ) / ( a + 1 );
xx = x * x;
nk = 2 * N + 1;
y = 1.0 / nk;
for( k = N; k > 0; k-- )
{
nk = nk - 2;
y = ( 1.0 / nk ) + ( xx * y );
}
return ( 2.0 * x * y );
}
/*------------------------------------------------------------------------------*/
/*!
* \brief tsp_ResistanceToTemperature
* \details Convert NTC resistance to temperature,
* important: Array sorting from large to small search
* \param[in] adc_val Current adc value
* \param[out] float32 Temperature( degree centigrade )
*/
/*------------------------------------------------------------------------------*/
static float32 tsp_ResistanceToTemperature( uint16 adc_val )
{
float32 B_value = TSP_NTC_B_VALUE;
float32 Rp_value = TSP_NTC_RATED_RES;
float32 T1 = 0.0F;
float32 T2 = TSP_NTC_T2_VALUE;
float32 Rt_value = 0.0F;
float32 volt_val = 0.0F;
/* Data anomaly judgment */
if( adc_val <= TSP_SHORT_CIRCUIT_THRESHOLD )
{
return 1.0F;
}
else if( adc_val >= TSP_OPEN_CIRCUIT_THRESHOLD )
{
return 2.0F;
}
else
{
/* MISRA-C coding rules */
}
/* Convert to voltage */
volt_val = ((float32) adc_val * TSP_ADC_VOLTAGE_REF) / TSP_ADC_FULL_SCALE;
/* Get the NTC resistance value */
Rt_value = volt_val / ( ( TSP_ADC_VOLTAGE_REF - volt_val ) / TSP_NTC_RATED_RES );
/* Operational formula */
T1 = ( 1.0F / ( ( log( Rt_value / Rp_value ) / B_value ) + ( 1.0F / T2 ) ) );
/* Operational formula */
// T1 = ( 1.0F / ( ( tsp_ln( Rt_value / Rp_value ) / B_value ) + ( 1.0F / T2 ) ) );
/* Kelvin value convert to degree celsius value */
T1 = T1 - TSP_NTC_KELVIN_VALUE;
return ( T1 );
}
#endif
注意：如果用于单片机程序，使用 <math.h>，且不开优化( -O1, -O2, -O3…)的话，程序会额外占用5KB的flash空间。开了程序优化，则可以正常使用math库中的log函数，不会额外占用flash空间。
当然，如果不想开优化，但是又想使用ln函数，可以自己实现。
double tsp_ln(double a)
该函数就是一种实现ln的算法。实际测试对比基本符合log函数功能
总结：
查表法与B值公式法两者测量温度对比：
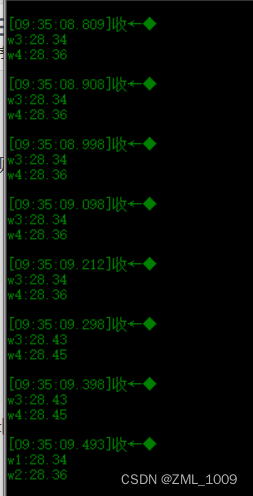
可以发现两者结果基本一致，只有小数点后第二位有0.01~0.02的误差，对于NTC采样来讲是可以接受的
我个人比较喜欢使用B值公式法，这样不用生成查表的表格，只需要将宏定义对应的关键参数进行配置，就可以满足不同规格的NTC电阻。
PS: 如何转换摄氏度为开尔文：
0摄氏度等于273.15开尔文 0℃ = 273.15K
例：将20℃转换为开尔文
T(K) = 20℃ + 273.15 = 293.15K
