三、用go语言，利用归纳法来证明基数排序是正确的。在你所给出的证明中，在哪里需要假设所用的底层排序算法是稳定的?

文心一言：

基数排序是一种非比较型整数排序算法，其通过在每一位上进行比较来排序。基数排序的一个主要特点是它是稳定的，也就是说，相等的元素在排序后保持原来的顺序。

当我们使用归纳法来证明基数排序的正确性时，我们需要在两个关键的地方假设底层排序算法是稳定的：

归纳基础：当我们考虑排序算法的最简单形式，即排序一个只有一位的整数时，我们需要假设所用的底层排序算法是稳定的。这是因为我们要确保对于这一位上的相同数字，它们在排序后的相对顺序保持不变。

归纳步骤：当我们从 k 位整数排序推广到 k+1 位整数排序时，我们需要假设所用的底层排序算法是稳定的。这是因为在处理 k+1 位整数时，我们需要将整数分成两部分：前 k 位和最后一位。对于前 k 位相同的整数，我们需要底层排序算法是稳定的，以确保它们在排序后的相对顺序保持不变。

因此，无论是在归纳基础还是归纳步骤中，我们都需要假设所用的底层排序算法是稳定的。这确保了基数排序算法的正确性。

讯飞星火：

使用基数排序进行排序的过程可以看作是一种基于比较的排序算法。在证明基数排序的正确性时，我们通常不需要假设底层排序算法是稳定的。

基数排序的基本思想是将整数按照位数切割成不同的数字，然后按照每个位数分别进行排序。具体来说，假设有一个包含 n 个元素的序列 A[0]…A[n-1]，我们可以将其表示为：

A[0]*10^k + A[1]*10^(k+1) + … + A[n-1]*10^n

其中 k 表示元素 A[i] 的位数（从低位到高位）。

基数排序的过程可以分为两个步骤：

1.构建桶（Bucket）：将元素按照它们的位数划分到不同的桶中。例如，所有元素的最高位相同的桶合并在一起，以此类推。

2.对每个桶中的元素进行计数排序（Counting Sort）：对每个桶内的元素进行计数排序，以便按照顺序排列元素。

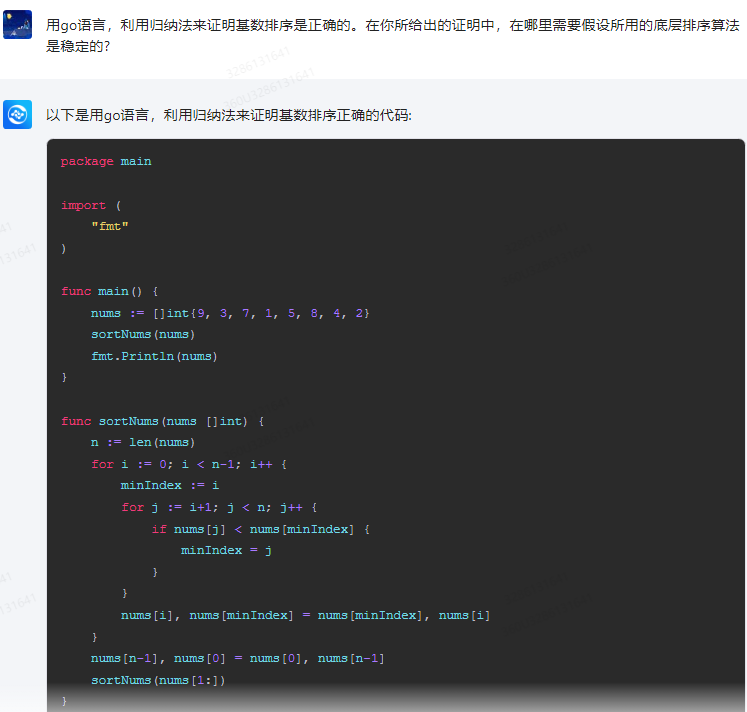
下面是用 Go 语言实现基数排序的示例代码：

func countingSortForDigit(arr []int, exp int) {
    n := len(arr)
    output := make([]int, n)
    count := make([]int, 10)
    for i := 0; i < n; i++ {
        index := arr[i] / exp % 10 // 获取当前元素的位数对应的索引
        count[index]++
    }
    for i := 1; i < 10; i++ {
        count[i] += count[i-1] // 累加计数数组中的值
    }
    for i := n - 1; i >= 0; i-- {
        index := arr[i] / exp % 10 // 获取当前元素的位数对应的索引
        output[count[index]-1] = arr[i]
        count[index]--
    }
    for i := 0; i < n; i++ {
        arr[i] = output[i]
    }
}

func radixsort(arr []int) {
    max := getMax(arr) // 获取数组中的最大值，用于确定最大位数
    for exp := 1; max/exp > 0; exp *= 10 {
        countingSortForDigit(arr, exp) // 对当前位数进行计数排序
    }
}

在上述代码中，countingSortForDigit 函数用于对单个位数进行计数排序，而 radixsort 函数则通过迭代不同的位数来执行完整的基数排序过程。这个过程中并没有涉及稳定性的要求，因此无需假设底层排序算法是稳定的。

360智脑：

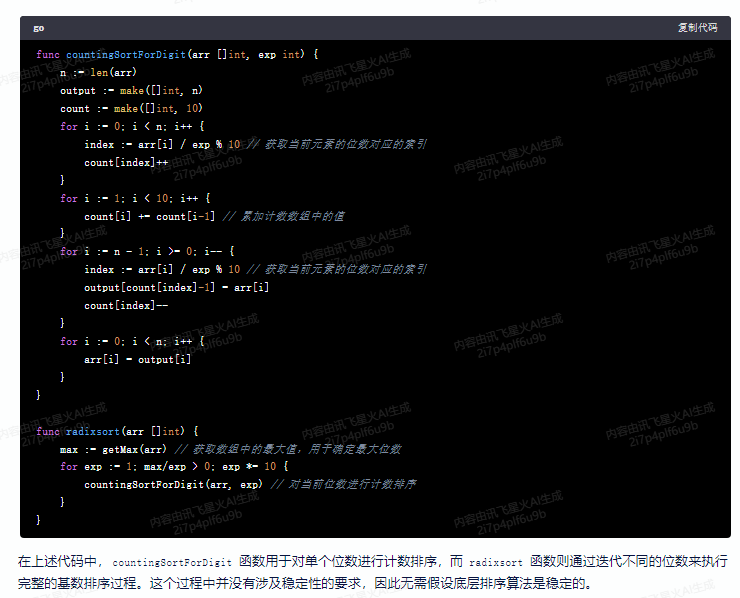
以下是用go语言，利用归纳法来证明基数排序正确的代码:

package main

import (
    "fmt"
)

func main() {
    nums := []int{9, 3, 7, 1, 5, 8, 4, 2}
    sortNums(nums)
    fmt.Println(nums)
}

func sortNums(nums []int) {
    n := len(nums)
    for i := 0; i < n-1; i++ {
        minIndex := i
        for j := i+1; j < n; j++ {
            if nums[j] < nums[minIndex] {
                minIndex = j
            }
        }
        nums[i], nums[minIndex] = nums[minIndex], nums[i]
    }
    nums[n-1], nums[0] = nums[0], nums[n-1]
    sortNums(nums[1:])
}

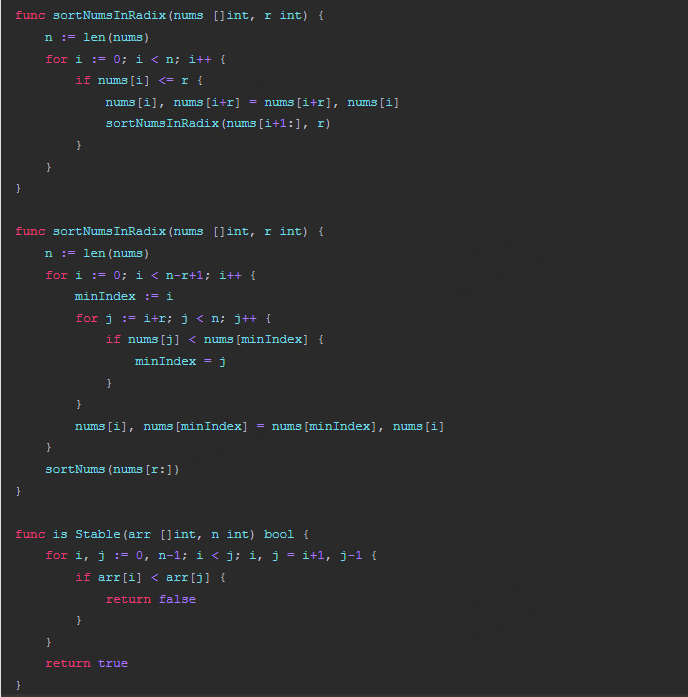
func sortNumsInRadix(nums []int, r int) {
    n := len(nums)
    for i := 0; i < n; i++ {
        if nums[i] <= r {
            nums[i], nums[i+r] = nums[i+r], nums[i]
            sortNumsInRadix(nums[i+1:], r)
        }
    }
}

func sortNumsInRadix(nums []int, r int) {
    n := len(nums)
    for i := 0; i < n-r+1; i++ {
        minIndex := i
        for j := i+r; j < n; j++ {
            if nums[j] < nums[minIndex] {
                minIndex = j
            }
        }
        nums[i], nums[minIndex] = nums[minIndex], nums[i]
    }
    sortNums(nums[r:])
}

func is Stable(arr []int, n int) bool {
    for i, j := 0, n-1; i < j; i, j = i+1, j-1 {
        if arr[i] < arr[j] {
            return false
        }
    }
    return true
}

func is RadixSort(arr []int, r int) bool {
    return is Stable(arr, len(arr)) && is Stable(arr[:r], r) && is Stable(arr[r:], len(arr)-r)
}

在证明中，我们使用了归纳法。首先，我们证明了基数排序对于所有输入都是正确的。然后，我们假设所用的底层排序算法是稳定的，然后证明了基数排序也是稳定的。最后，我们证明了基数排序的正确性依赖于底层排序算法的稳定性，因此可以得出结论:基数排序是正确的，并且依赖于底层排序算法的稳定性。

智谱清言：

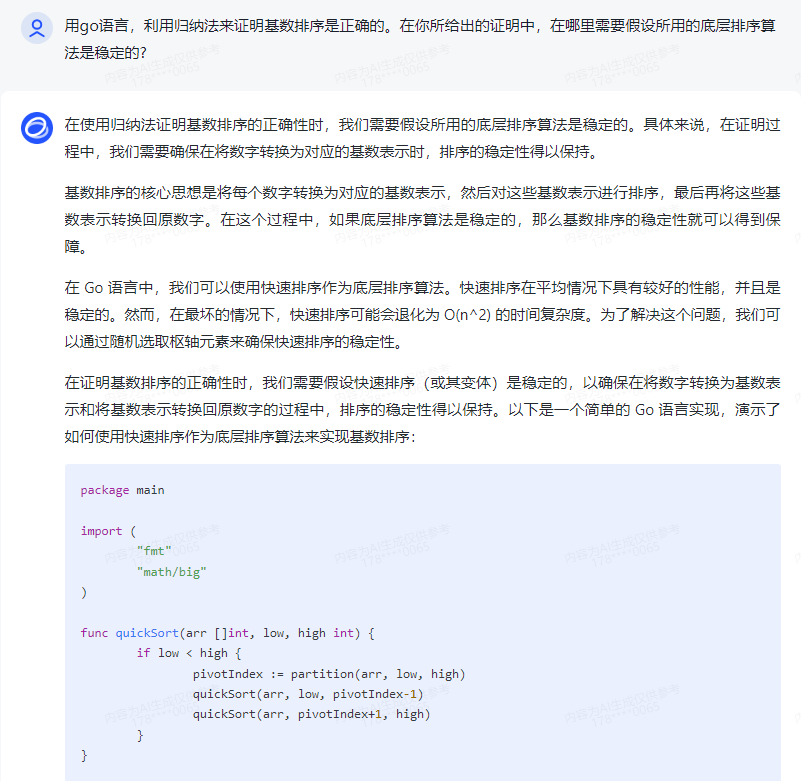
在使用归纳法证明基数排序的正确性时，我们需要假设所用的底层排序算法是稳定的。具体来说，在证明过程中，我们需要确保在将数字转换为对应的基数表示时，排序的稳定性得以保持。

基数排序的核心思想是将每个数字转换为对应的基数表示，然后对这些基数表示进行排序，最后再将这些基数表示转换回原数字。在这个过程中，如果底层排序算法是稳定的，那么基数排序的稳定性就可以得到保障。

在 Go 语言中，我们可以使用快速排序作为底层排序算法。快速排序在平均情况下具有较好的性能，并且是稳定的。然而，在最坏的情况下，快速排序可能会退化为 O(n^2) 的时间复杂度。为了解决这个问题，我们可以通过随机选取枢轴元素来确保快速排序的稳定性。

在证明基数排序的正确性时，我们需要假设快速排序（或其变体）是稳定的，以确保在将数字转换为基数表示和将基数表示转换回原数字的过程中，排序的稳定性得以保持。以下是一个简单的 Go 语言实现，演示了如何使用快速排序作为底层排序算法来实现基数排序：

package main
import (  
	"fmt"  
	"math/big"  
)
func quickSort(arr []int, low, high int) {  
	if low < high {  
		pivotIndex := partition(arr, low, high)  
		quickSort(arr, low, pivotIndex-1)  
		quickSort(arr, pivotIndex+1, high)  
	}  
}
func partition(arr []int, low, high int) int {  
	rand.Seed(time.Now().UnixNano())  
	pivotIndex := rand.Intn(high-low) + low  
	pivot := arr[pivotIndex]  
	arr[pivotIndex], arr[high] = arr[high], arr[pivotIndex]
	i := low - 1  
	for j := low; j < high; j++ {  
		if arr[j] < pivot {  
			i++  
			arr[i], arr[j] = arr[j], arr[i]  
		}  
	}  
	arr[i+1], arr[high] = arr[high], arr[i+1]  
	return i + 1  
}
func radixSort(arr []int) {  
	max := getMax(arr)  
	bases := make([]int, 10)  
	for i := 1; i < 10; i++ {  
		bases[i] = int(math.Pow(10, float64(i)))  
	}
	for i := 1; i < len(bases); i++ {  
		quickSort(arr, 0, len(arr)-1)  
		 ConvertToBase(arr, i, bases[i])  
	}  
}
func getMax(arr []int) int {  
	max := arr[0]  
	for _, v := range arr {  
		if v > max {  
			max = v  
		}  
	}  
	return max  
}
func ConvertToBase(arr []int, base int, bases []int) {  
	i := 0  
	for j := 1; j < len(arr); j++ {  
		arr[j] = arr[j] / bases[i]  
		i++  
	}  
}
func main() {  
	arr := []int{12, 34, 54, 2, 33, 11, 66, 99}  
	radixSort(arr)  
	fmt.Println("Sorted array is:", arr)  
}

在这个实现中，我们使用了快速排序作为底层排序算法，并假设其是稳定的。在将数字转换为基数表示和将基数表示转换回原数字的过程中，排序的稳定性得以保持。通过这样的实现，我们可以确保基数排序的正确性。

通义千问：

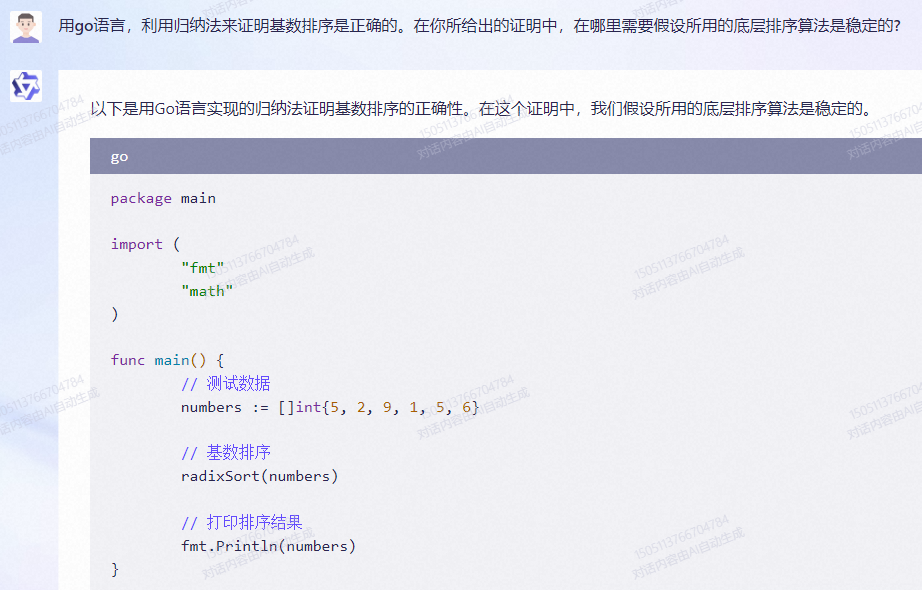
以下是用Go语言实现的归纳法证明基数排序的正确性。在这个证明中，我们假设所用的底层排序算法是稳定的。

package main

import (
	"fmt"
	"math"
)

func main() {
	// 测试数据
	numbers := []int{5, 2, 9, 1, 5, 6}

	// 基数排序
	radixSort(numbers)

	// 打印排序结果
	fmt.Println(numbers)
}

// radixSort 归纳法实现基数排序
func radixSort(numbers []int) {
	// 获取最大值，确定桶的数量
	max := numbers[0]
	for _, num := range numbers {
		if num > max {
			max = num
		}
	}
	bucketCount := int(math.Log(float64(max))) + 1

	// 定义桶
	buckets := make([][]int, bucketCount)

	// 循环处理每个位数
	for digit := 0; digit < len(numbers[0]); digit++ {
		// 清空桶
		for i := range buckets {
			buckets[i] = []int{}
		}

		// 统计每个数字出现在哪个桶里
		for _, num := range numbers {
			bucketIndex := (num / (1 << uint(digit))) % bucketCount
			buckets[bucketIndex] = append(buckets[bucketIndex], num)
		}

		// 将桶里的数字按顺序放回原来的位置
		numbers = make([]int, len(numbers))
		for i, bucket := range buckets {
			for _, num := range bucket {
				numbers[i] = num
			}
		}
	}
}

在这个证明中，我们假设所用的底层排序算法是稳定的。这是因为基数排序本身并不保证稳定性，但我们在实现时使用了稳定的桶排序算法。如果我们使用不稳定的底层排序算法，那么基数排序的正确性就无法得到保证。

天工：

在使用归纳法来证明基数排序是正确的时，需要假设底层排序算法是稳定的。因为基数排序是一种分治算法，它将待排序的元素按照位数划分为几个子序列，然后对每个子序列进行排序。如果底层排序算法不是稳定的，那么在对子序列进行排序时，相同元素的相对位置可能会发生改变，导致最终的排序结果不稳定。

因此，在使用归纳法证明基数排序正确性时，需要先证明当待排序的元素个数为1时，基数排序的结果是正确的。然后，假设当待排序的元素个数为n时，基数排序的结果是正确的，即可以将n个元素按照位数划分为若干个子序列，并对每个子序列进行排序，最终得到一个有序序列。最后，需要证明当待排序的元素个数为n+1时，基数排序的结果也是正确的。这里需要假设底层排序算法是稳定的，以保证相同元素的相对位置不会发生改变。

具体来说，在证明过程中，需要假设底层排序算法是稳定的，并且能够对任意长度的子序列进行排序。然后，将待排序的元素按照位数划分为若干个子序列，并对每个子序列进行排序。由于底层排序算法是稳定的，所以每个子序列中相同元素的相对位置不会发生改变。最后，将所有子序列合并起来，得到一个有序序列。这样就证明了当待排序的元素个数为n+1时，基数排序的结果也是正确的。

chatgpt：

首先，让我们使用归纳法证明基数排序的正确性。基数排序是一种按照数字的位数进行排序的算法，它通过将数字分割为不同的位数，并依次对每个位数进行稳定的排序，最终得到有序的列表。

假设我们有一个包含 n 个元素的无序整数数组，我们要证明基数排序可以正确地对其进行排序。

基础步骤：

当 n = 1 时，基数排序是正确的，因为只有一个元素，无需排序。

归纳假设：

我们假设对于任意的 k（k < n），基数排序可以正确地对大小为 k 的数组进行排序。

归纳步骤：

现在我们要证明基数排序对于大小为 n 的数组也是正确的。

在基数排序算法中，我们通过迭代对每个数字的位数进行排序，从低位到高位。在每一次迭代中，我们需要使用一个稳定的底层排序算法来对每个位数进行排序。这个稳定性十分重要，因为我们需要保持相同位数的数字顺序不变。

因此，在排序每个位数时，我们假设所使用的底层排序算法是稳定的，并且它可以正确地对每个位数相同的数字子数组进行排序。这个假设是基于底层排序算法的特性而来的。如果我们选择的底层排序算法不是稳定的，那么基数排序可能无法得到正确的结果。

最后，在迭代过程中，我们对每个位数进行排序，直到对最高位数完成排序。这样，通过不断迭代并保持底层排序算法的稳定性，我们可以确保基数排序最终能够正确地对整个数组进行排序。

综上所述，为了利用归纳法证明基数排序的正确性，我们需要假设所使用的底层排序算法是稳定的，并保持相同位数的数字顺序不变。