这俩月终于结束了233333,之后就是反复复习和背八股了吧,然后整整项目春招再投投投,感觉大部分题都有思路了但是做过的题也会没思路,还是要复习
总结
数组:
双指针用的很多,一般一个指向遍历位置,另一个指向插入位置
链表:
也是双指针比较多,注意可以创造一个dummy节点指向头节点,从dummy开始遍历会比较方便;环形链表位置是快慢指针,快走2慢走1,它们肯定会在慢没走完环的一圈时相遇,此时把慢指针放在头节点,两个指针同步走,相等的位置即环入口
哈希:
unordered_map; unordered_set;解决字母异位词,几数之和等;去重常用set;map一般key保存值,value保存下标
栈和队列:
有效的括号,栈和队列互相实现
二叉树:
两种,迭代(层序)和递归(深度);迭代时是用一个队列保存节点,记录每层节点数size,当pop节点时,size--(到0时该层结束),并把他的左右孩子进入队列;
递归:
-
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
-
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
-
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
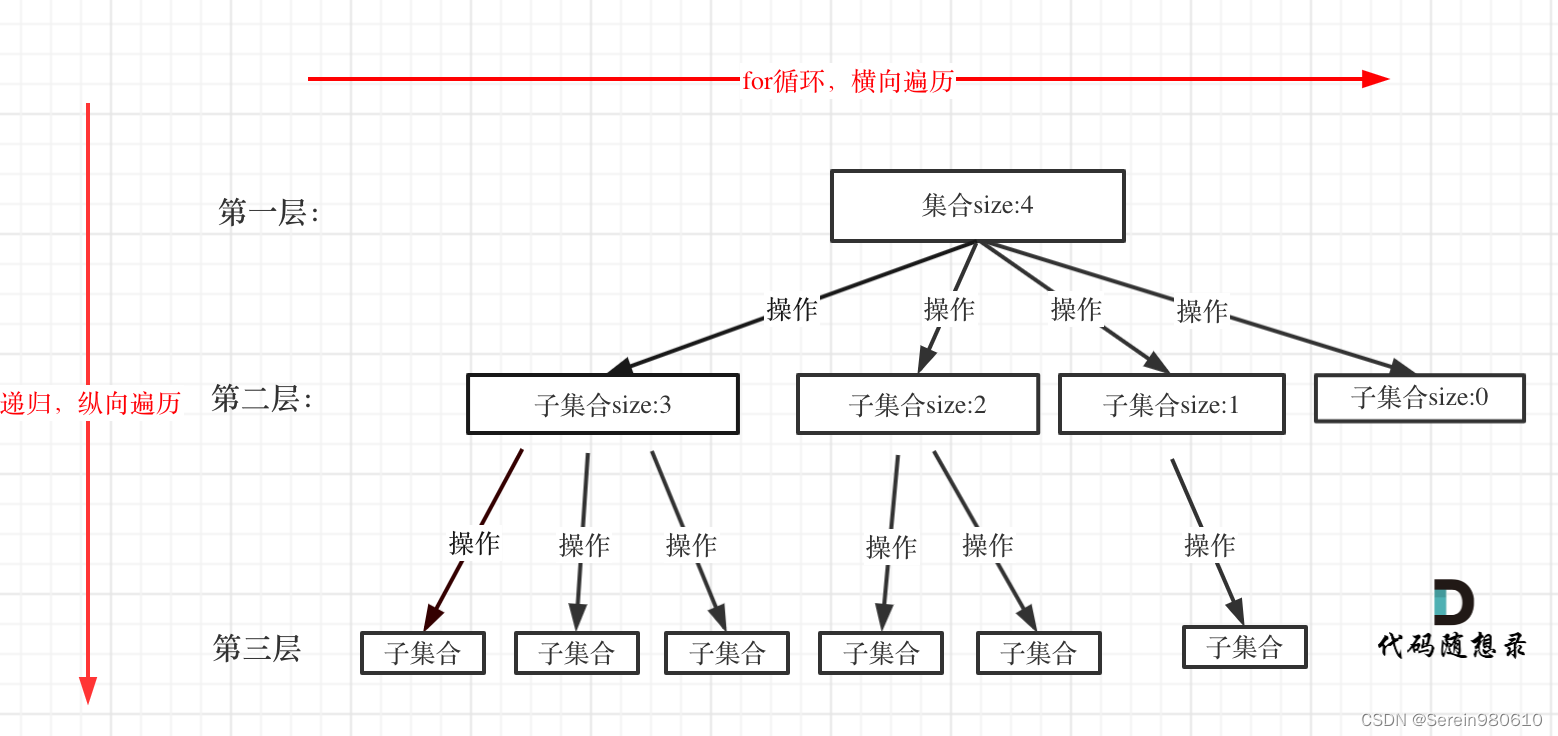
回溯:
三要素
回溯函数模板返回值以及参数
回溯函数终止条件
回溯搜索的遍历过程
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
贪心:
没有套路,大概就是局部最优可以推到全局最优
动规:
-
确定dp数组(dp table)以及下标的含义
-
确定递推公式
-
dp数组如何初始化
-
确定遍历顺序
-
举例推导dp数组
最重要的还是01背包和完全背包,是指有物品i,重量为weight[i],价值为value[i],装满这个背包所能得到的最大价值;dp[i][j]为取【0,i】物品时[重量为j]的最大价值;
01: dp[i][j] =max( dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] ) // 不取i但重量为j的价值和取i重量为j的最大值
压成一维数组
dp[j] =max( [j] , dp[j-weight[i]] + value[i] )// 每一层的dp是由上一层的dp来的,所以只需要一维就可以了,注意第二层for要从后往前遍历,保证物品i只被放入一次!
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}完全背包:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}