一:二叉搜索树
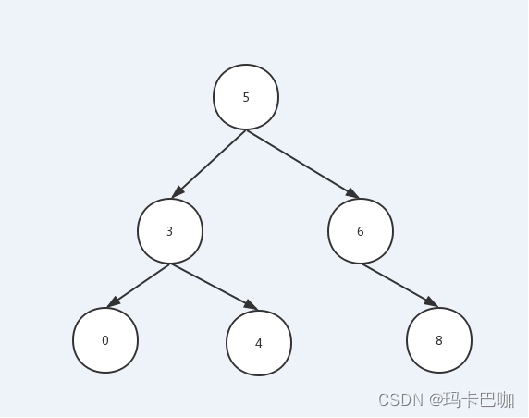
大家来看以下几个结构:下图中的 二叉搜索树又叫二叉查找树,二叉排序树;
它具有以下特点:
1.如果它的左子树不为空,则左子树上结点的值都小于根结点。
2.如果它的右子树不为空,则右子树上结点的值都大于根结点。
3.子树同样也要遵循以上两点
为什么又叫做二叉排序树呢?
二叉树的遍历方式:前 中 后 层次(Mysql)
只要一颗树是二叉搜索树,那么它的中序遍历一定是有序的。
左根(输出)右 看右边的这颗二叉树,它的中序遍历为:左根右 左 根(输出) 右:0 3 4 5 6 8
就是比较像二叉查找算法:猜数字,0~100出一个数,让你猜。每次会告诉你猜的结果是大了还是小了。 50 大了-> 51~100 小了 0~50每次一猜就可以排除一半的空间.归并排序,logn;有序的序列
二:二叉搜索树的增删改查
二叉搜索插入 5 3 6 0 4 8
插入的时候每次都是和根结点比较。一直要找到它应该插入的位置。 肯定会插在叶子结点。
那么其实大家可以看到 插入其实就是查找。
增改查: 简单,主要是删除
删除 是要分三种情况
1.要删除的结点是叶子结点 O(1)
2.要删除的结点只有一个子树(左或者右)O(1)
3.要删除的结点有两颗子树:找后继结点,而且后继结点的左子树一定为空。
说明:这里的后继结点不是要删除的右边第一个结点,而是比它大的第一个结点,否则就不符合二叉搜索树的规则,无法排序,当这个后继结点只有一个子结点的时候就相当于删除的第二种情况。所以就引入了红黑树!
性能:
查找 logn
插入:nlogn 有n个数要插入,每一个都要先查找到它的位置 就是logn 合起来就是nlogn,插入单个肯定是logn
三:二叉树的应用
二叉搜索树有哪些应用呢?
O(n) for(int i = 0 ; i < n ; i++){} 像下图这个也是二叉树,只不过插入的是有序数列,所以为了防止这种现象,就出现了平衡二叉树,在中间隔开。弊端退化成链表了 既然是搜索树,那么肯定就是用在了查找上。 我们来分析它的查找时间复杂度: 看右边两颗二叉搜索树: 他们的性能: 查找时间复杂度其实就是树的深度 O(n)表示时间复杂度:查找N次。循环了N遍 为什么(退化了)?怎么解决呢? 不要变成一个链条一样
AVL树(绝对平衡树): 红黑树和平衡二叉树:AVL属于实验室状态的,红黑树才是我们项目中用的。
3.1 二叉代码
package tree;
public class BinarySeachTree {
private int color = 0; //0表示黑,1表示红
int data;
BinarySeachTree left;
BinarySeachTree right;
BinarySeachTree parent;
public BinarySeachTree(int data) {
this.data = data;
this.left = null;
this.parent = null;
this.color = 1;
this.right = null;
//parent.parent ;爷爷
//parent.parent.left 左边的叔叔
//parent.left 兄弟姐妹
}
//插入的时候每次都是和根结点比较。一直要找到它应该插入的位置。
//肯定会插在叶子结点。那么其实大家可以看到 插入其实就是查找。 默认root不会为空
public void insert(BinarySeachTree root,int data) {
//if(root == null) {}
if(root.data < data) { //根节点小 我们要放到右边
if(root.right == null) {
root.right = new BinarySeachTree(data);
}else {
insert(root.right, data);
}
}else {
if(root.left == null) {
root.left = new BinarySeachTree(data);
}else {
insert(root.left, data);
}
}
}
public void find(BinarySeachTree root,int data) {
if(root != null) {
if(root.data < data) {
find(root.right, data);
}else if(root.data > data) {
find(root.left, data);
}else {
System.out.println("找到了");
System.out.println(root.data);
return ;
}
}
}
public void pre() {
}
public void post() {
}
public void in(BinarySeachTree root) { //中序遍历
if(root != null) {
in(root.left);
System.out.print(root.data + " ");
in(root.right);
}
}
public static void main(String[] args) {
//快速排序,归并排序,二叉树排序
int data[] = {0,5,9,1,2,3,10};
BinarySeachTree root = new BinarySeachTree(data[0]); //第一个点作为跟结点
for(int i = 1 ; i < data.length ; i ++) {
root.insert(root, data[i]);
}
System.out.println("中序遍历:");
root.in(root);
}
}
四:引入红黑树(性质,左旋,右旋)
通过上面两个图我们发现,二叉树的结构就决定了其搜索的性能,那么我们应该怎么优化呢?
因此就有了AVL树和红黑树
AVL树:平衡二叉树,它的左右子树高度之差不超过1 这样确实可以避免一条直线型的结构,但还不是我们最理想的
可以认为是理想状态,实验室。红黑树
为什么呢? 通过性能综合考虑选用:
红黑树的性质(重点):
1.每个结点不是红色就是黑色
2.不可能有连在一起的红色结点(黑色的就可以),每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据
3.根结点都是黑色 root 4.每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
4.2 红黑树的三种变换
1.改变颜色:最简单 红变黑 黑变红
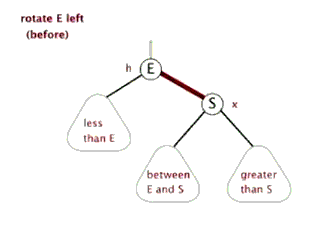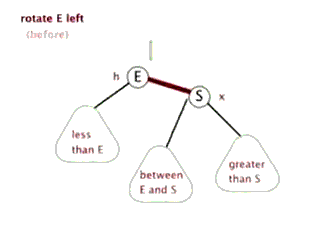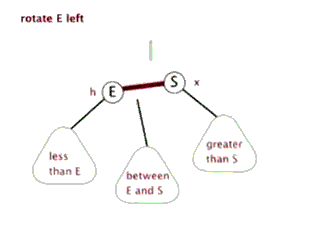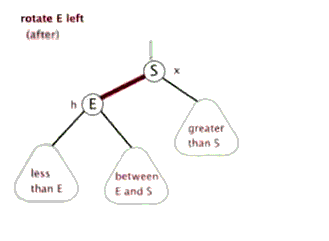
2.左旋:针对于点旋,但是点上面的子树也要跟着转。指针
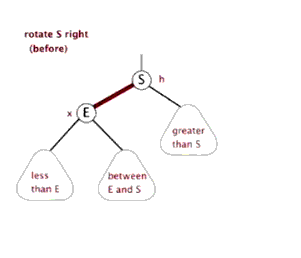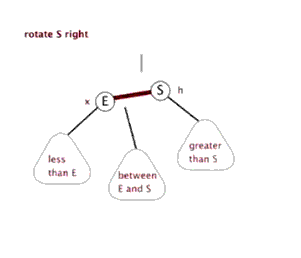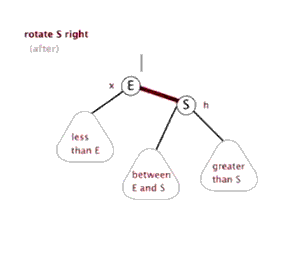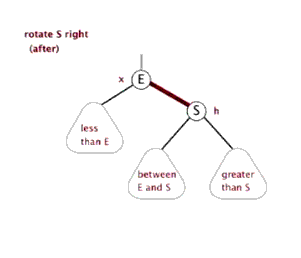
3.右旋:
那么我们又该如何选择以上三种方式呢?
4.3 插入规则
插入的时候旋转和颜色变换规则:
1.变颜色的情况:当前结点的父亲是红色,且它的祖父结点的另一个子结点 也是红色。(叔叔结点): (1)把父节点设为黑色 (2)把叔叔也设为黑色 (3)把祖父也就是父亲的父亲设为红色(爷爷) (4)把指针定义到祖父结点(爷爷)设为当前要操作的.
2.左旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是右子树。左旋 以父结点作为左旋。指针变换到父亲结点
3.右旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是左子树。右旋 (1)把父结点变为黑色 (2)把祖父结点变为红色 (爷爷) (3)以祖父结点旋转(爷爷)
红黑树的删除: 红黑树的删除讲实话是最难的,这里我不作必须掌握的要求,但是你必须要掌握二叉搜索的删除原理。因为,即便你将左右旋背得滚瓜烂熟,我保证你过不几天就忘光了。学习红黑树的代码实现,对于你平时做项目开发没有太大帮助。 对于大部分人来说,这辈子你可能都不会亲手写红黑树。而且,它对于算法面试也几乎没什么用,一般情况下,正常的人也不会要你手写红黑树,最多只会问你一下原理,但是二叉搜索树就是必须要掌握的了,这个我在面试中就可能会要你写伪代码。
红黑树的性能分析 插入 近似:nlogn 查找 logn 删除:近似logn
红黑树的应用: 1.HashMap 2.TreeMap 3.Windows底层:查找 4.Linux进程调度,nginx等