基本概念
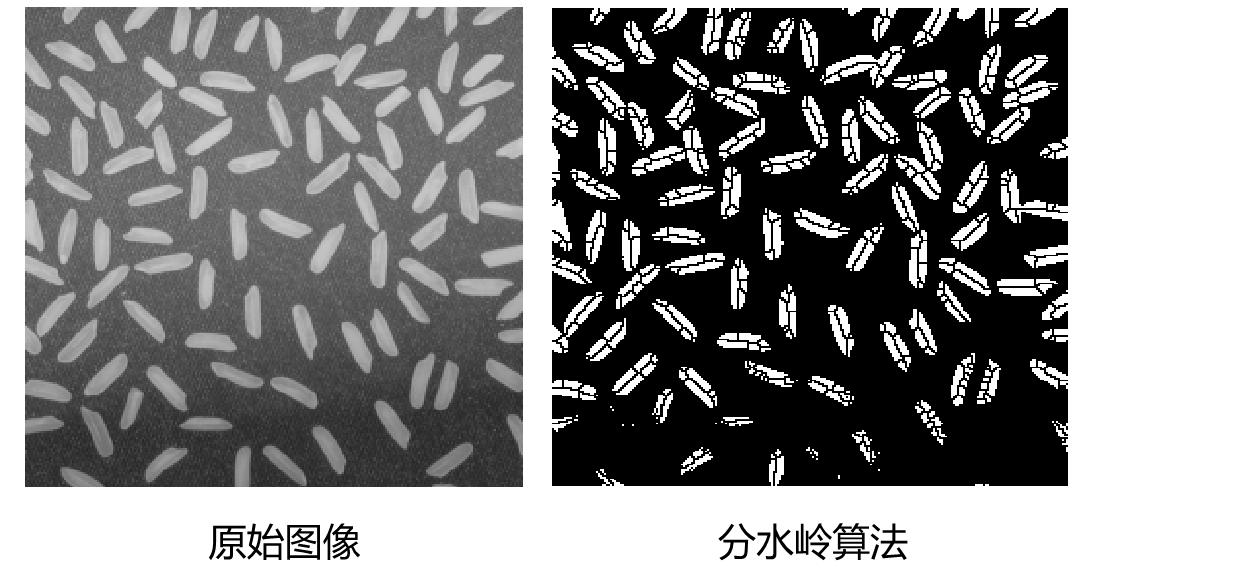
最常用的分水岭算法是F.Meyer在20世纪90年代早期提出的基于灰度图像的分割算法,它是一种基于拓扑理论的数学形态学的分割方法,其基本思想是把图像看作是测地学上的拓扑地貌,图像中每一点像素的灰度值表示该点的海拔高度,每一个局部极小值及其影响区域称为集水盆,而集水盆的边界则形成分水岭。分水岭的概念和形成可以通过模拟浸入过程来说明。在每一个局部极小值表面,刺穿一个小孔,然后把整个模型慢慢浸入水中,随着浸入的加深,每一个局部极小值的影响域慢慢向外扩展,在两个集水盆汇合处构筑大坝,即形成分水岭。
示例代码
filename = 'rice.png';%filename = 'g:\pear1.jpg'
f = imread(filename);%f = imread('g:\rice.png');
figure(1),imshow(f)
info = imfinfo(filename);
if info.BitDepth>8
f = rgb2gray(f);
end
b = im2bw(f,graythresh(f)); %二值化,注意应保证集水盆地的值较低(为0),否则就要对b取反
d = bwdist(b); %求零值到最近非零值的距离,即集水盆地到分水岭的距离
I = watershed(-d); %MATLAB自带的分水岭算法,I中的零值即为分水岭
w = (I == 0); %取出边缘
g = b&(~w); %用w作为mask从二值图像中取值
figure,imshow(g);