算法通关村第十九关——动态规划高频问题(白银)
- 前言
- 1 最少硬币数
- 2 最长连续递增子序列
- 3 最长递增子序列
- 4 完全平方数
- 5 跳跃游戏
- 6 解码方法
- 7 不同路径 II
前言
摘自:代码随想录
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
- 确定递推公式
- 初始化dp数组
- 确定遍历顺序
- 举例推导dp数组
1 最少硬币数
leetcode 322. 零钱兑换
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为 j 所需钱币的最少个数为dp[j]
- 确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],
那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
int[] dp = new int[amount + 1];
// 往数组dp里面填充某个数,这里选择amount+1,就是最大的值
Arrays.fill(dp, amount+1);
dp[0] = 0;
- 确定遍历顺序
有两种方式:
第一种:外循环遍历金额,内循环遍历硬币面额。
第二种:外循环遍历硬币面面额,内循环遍历金额。
这两种遍历顺序对应的意义如下:
-
外循环遍历金额,内循环遍历硬币面额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑金额的变化,然后再考虑不同的硬币面额。
也就是说,我们固定一个金额,尝试使用不同的硬币面额来找零。这样做的好处是可以利用之前已经计算出来的金额的最少硬币数,快速得到当前金额的最优解。由于金额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用前面较小金额的最优解已经被计算出来的特点。
// 遍历金额
for (int i = 1; i <= amount; i++) {
// 遍历硬币面额
for (int j = 0; j < coins.length; j++) {
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
}
}
}
-
外循环遍历硬币面额,内循环遍历金额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑不同的硬币面额,然后再考虑不同的金额。
也就是说,我们固定一个硬币面额,尝试在不同的金额下进行找零。这样做的好处是可以保证我们将所有可能的硬币面额都考虑到,并且在计算每个金额的最优解时,可以利用之前已经计算出来的较小金额的最优解。由于硬币面额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用之前较小硬币面额的最优解已经被计算出来的特点。
// 遍历硬币面额
for (int coin : coins){
// 遍历金额
for (int i = 1; i <= amount; i++) {
if(coin <= i){
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
全部代码如下:
第一种:
class Solution {
public int coinChange(int[] coins, int amount) {
// 初始化dp数组
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
// 遍历金额
for (int i=1; i <= amount; i++) {
// 遍历硬币面额
for (int j=0; j < coins.length; j++){
if(coins[j] <= i){
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
}
第二种:
class Solution {
public int coinChange(int[] coins, int amount) {
// 初始化dp数组
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
// 遍历硬币面额
for (int coin : coins){
// 遍历金额
for (int i = 1; i <= amount; i++) {
if(coin <= i){
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
}
2 最长连续递增子序列
leetcode 674. 最长连续递增序列
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp数组:表示以当前元素为结尾的最长连续递增序列的长度。
dp[i]表示以nums[i]为结尾的最长连续递增序列的长度。
- 确定递推公式
如果nums[i] > nums[i-1],则dp[i] = dp[i-1] + 1;否则dp[i] = 1。
- dp数组如何初始化
我们将dp数组的所有元素初始化为1,因为每个元素都可以作为一个单独的递增序列。
- 确定遍历顺序
从第二个元素开始遍历:
for(int i=0; i < nums.length; i++){
if(i > 0 && nums[i] > nums[i-1]){
dp[i] = dp[i-1] + 1;
}else{
dp[i] = 1;
}
}
- 举例说明
举例说明:给定数组nums = [1, 3, 5, 4, 7]。
遍历过程如下:
- 对于nums[1] = 3,nums[0] = 1 < nums[1],所以dp[1] = dp[0] + 1 = 2。
- 对于nums[2] = 5,nums[1] = 3 < nums[2],所以dp[2] = dp[1] + 1 = 3。
- 对于nums[3] = 4,nums[2] = 5 > nums[3],所以dp[3] = 1。
- 对于nums[4] = 7,nums[3] = 4 < nums[4],所以dp[4] = dp[3] + 1 = 2。
最终的最长连续递增序列的长度为dp数组的最大值,即为3。
最后代码如下:
class Solution {
public int findLengthOfLCIS(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
dp[0] = 1;
for(int i=1; i < nums.length; i++){
if(nums[i] > nums[i-1]){
dp[i] = dp[i-1] + 1;
}else{
dp[i] = 1;
}
}
return Arrays.stream(dp).max().getAsInt();
}
}
不是使用stream的方式:
class Solution {
public int findLengthOfLCIS(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
dp[0] = 1;
int maxLength = 1;
for(int i=1; i < nums.length; i++){
if(nums[i] > nums[i-1]){
dp[i] = dp[i-1] + 1;
}else{
dp[i] = 1;
}
maxLength = Math.max(maxLength, dp[i]);
}
return maxLength;
}
}
还可以得到dp[i],再遍历一遍得到最大值,这就不写了
3 最长递增子序列
leetcode 300. 最长递增子序列
-
确定dp数组(dp table)及其下标的含义:
- dp数组:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
- 下标的含义:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
-
确定递推公式:
- 如果nums[i] > nums[j],则:dp[i] = max(dp[i], dp[j] + 1)。
为啥呢??
这里的i和j表示数组
nums的索引。具体来说,i表示当前遍历到的元素的索引,而j表示在i之前的元素的索引。当我们遍历到第i个元素时,我们需要寻找在i之前的元素中比nums[i]小的元素。这样,我们就可以利用这个小于nums[i]的元素来构成一个更长的递增子序列。
所以,当nums[i] > nums[j]时,表示nums[i]比nums[j]大,我们可以将以j结尾的最长递增子序列的长度加1,然后与以i结尾的最长递增子序列的长度进行比较,取较大的值作为以i结尾的最长递增子序列的长度。也就是递推公式中的
dp[i] = max(dp[i], dp[j] + 1)。 -
初始化dp数组:
- 初始时,dp数组中的每个元素都设为1,因为最短的递增子序列长度为1。
-
确定遍历顺序:
- 外层循环遍历数组nums,从左到右依次计算dp[i]的值。
- 内层循环遍历数组nums,从数组开始到i的位置,寻找前面的数字nums[j]是否小于nums[i],如果是,则根据递推公式更新dp[i]的值。
-
举例推导dp数组:
如果nums[i] > nums[j],则dp[i] = max(dp[i], dp[j] + 1)。
逐个元素计算dp[i]的值:
- 当i = 1时,nums[i] = 9,此时没有比9小的元素,所以以9结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 2时,nums[i] = 2,此时在2之前有9和10两个元素,都比2大,所以以2结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 3时,nums[i] = 5,此时在5之前有2和9两个元素,其中2比5小,所以以5结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 1 1 1 1- 当i = 4时,nums[i] = 3,此时在3之前有2和5两个元素,其中2比3小,所以以3结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 2 1 1 1
后面略~~~~~~
完整代码如下:
class Solution {
public int lengthOfLIS(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
int[] dp = new int[n];
dp[0] = 1;
int result = 1;
for (int i = 1; i < n; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
result = Math.max(result, dp[i]);
}
return result;
}
}
4 完全平方数
leetcode 279. 完全平方数
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
**dp[i]:**表示数字i的最少完全平方数的个数。
- 确定递推公式
对于数字 i 来说,我们需要遍历所有小于等于 i 的完全平方数 j( j 从 1 到 sqrt(i) ),然后将当前数字 i 减去 j 得到差值,即 i - j 。我们需要找到 dp[ i - j * j ] 的最小值,然后再加上1(表示当前完全平方数 j ),即可得到dp[i]的值。
递推公式为:dp[i] = Math.min(dp[i], dp[i - j * j] + 1),其中 j * j <= i。
- 初始化dp数组
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
- 确定遍历顺序
// 遍历dp数组
for (int i = 1; i <= n; i++) {
// 遍历小于等于i的完全平方数j*j
for (int j = 1; j * j <= i; j++) {
// 更新dp[i]
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
- 举例推导dp数组
略。。。
完整代码:
class Solution {
public int numSquares(int n) {
// 定义dp数组
int[] dp = new int[n + 1];
// 初始化dp数组
Arrays.fill(dp, n+1);
dp[0] = 0;
// 遍历dp数组
for (int i = 1; i <= n; i++) {
// 遍历小于等于i的完全平方数j*j
for (int j = 1; j * j <= i; j++) {
// 更新dp[i]
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
}
}
当然,这个代码可以再优化一下:(使用Math的api)
减少内层循环的次数:对于小于等于 i 的完全平方数 j ,我们可以通过计算 i - j * j 的平方根得到 j 的最大值,并从最大值开始遍历,这样可以减少内层循环的次数。
class Solution {
public static int numSquares(int n) {
// 定义dp数组
int[] dp = new int[n + 1];
// 初始化dp数组
Arrays.fill(dp, n + 1);
dp[0] = 0;
// 遍历dp数组
for (int i = 1; i <= n; i++) {
// 获取当前数字i的最大完全平方数j*j
int maxSquare = (int) Math.sqrt(i);
// 遍历完全平方数j*j
for (int j = maxSquare; j >= 1; j--) {
// 更新dp[i]
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
}
}
5 跳跃游戏
leetcode 55. 跳跃游戏
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从起点位置到达位置i时能否跳跃到最后一个位置。
- 确定递推公式
dp[i] = (dp[j] && nums[j] >= i - j),其中0 <= j < i
- 初始化dp数组
初始化dp数组所有位置为false。
- 确定遍历顺序
外层循环遍历i从1到n-1,内层循环遍历j从0到i-1。
- 举例推导dp数组
以数组nums = [2, 3, 1, 1, 4]为例进行推导:
初始状态:
dp = [false, false, false, false, false]
推导dp[1]:
dp[1] = (dp[0] && nums[0] >= 1 - 0) = (false && 2 >= 1) = false
推导dp[2]:
dp[2] = (dp[0] && nums[0] >= 2 - 0) || (dp[1] && nums[1] >= 2 - 1) = (false && 2 >= 2) || (false && 3 >= 2) = false
推导dp[3]:
dp[3] = (dp[0] && nums[0] >= 3 - 0) || (dp[1] && nums[1] >= 3 - 1) || (dp[2] && nums[2] >= 3 - 2) = (false && 2 >= 3) || (false && 3 >= 3) || (false && 1 >= 3) = false
完整代码如下:
class Solution {
public boolean canJump(int[] nums) {
// 获取数组长度
int n = nums.length;
// 定义dp数组
boolean[] dp = new boolean[n];
// 初始化dp数组
dp[0] = true;
// 遍历dp数组
for (int i = 1; i < n; i++) {
// 内层循环遍历j
for (int j = 0; j < i; j++) {
// 更新dp[i]
dp[i] = dp[j] && nums[j] >= i - j;
// 如果dp[i]为true,则跳出内层循环
if (dp[i]) {
break;
}
}
}
return dp[n - 1];
}
}
6 解码方法
leetcode 91. 解码方法
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从字符串的起始位置到第i个字符时的解码方法总数。
- 确定递推公式
对于dp数组中的每个位置i,我们需要考虑两个情况:
- 如果第i个字符能够单独解码(即不为0),则dp[i] = dp[i-1],因为第i个字符自身可以作为一个解码方法;
- 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间),则dp[i] += dp[i-2],因为组成的两位数可以作为一个解码方法。
则,递推公式为:dp[i] = dp[i-1] + dp[i-2],其中0 <= i < n。
- 初始化dp数组
初始化dp数组的长度为n+1,初始值为0。
- 确定遍历顺序
for (int i = 1; i <= n; i++) {
// 如果第i个字符能够单独解码(即不为0)
if (s.charAt(i - 1) != '0') {
dp[i] += dp[i - 1];
}
// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)
if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {
dp[i] += dp[i - 2];
}
}
// 判断字符串编码是否在1到26之间
private static boolean isValidEncoding(String s) {
if (s.charAt(0) == '0') {
return false;
}
int num = Integer.parseInt(s);
return num >= 1 && num <= 26;
}
- 举例推导dp数组
以字符串s = "226"为例进行推导:
初始状态:
dp = [1, 0, 0, 0]
推导dp[1]:
如果第1个字符为2,能够单独解码为"2",所以dp[1] = dp[0] = 1
推导dp[2]:
如果第2个字符为2,能够单独解码为"2",所以dp[2] = dp[1] = 1
如果第1个字符与第2个字符组成的两位数为26,能够解码为"26",所以dp[2] += dp[0],即dp[2] = dp[1] + dp[0] = 1 + 1 = 2
推导dp[3]:
如果第3个字符为6,能够单独解码为"6",所以dp[3] = dp[2] = 2
如果第2个字符与第3个字符组成的两位数为26,能够解码为"26",所以dp[3] += dp[1],即dp[3] = dp[2] + dp[1] = 2 + 1 = 3
最终结果:
dp = [1, 1, 2, 3]
完整代码:
class Solution {
public static int numDecodings(String s) {
// 获取字符串的长度
int n = s.length();
// 定义dp数组
int[] dp = new int[n + 1];
// 初始化dp数组
dp[0] = 1;
// 遍历dp数组
for (int i = 1; i <= n; i++) {
// 如果第i个字符能够单独解码(即不为0)
if (s.charAt(i - 1) != '0') {
dp[i] += dp[i - 1];
}
// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)
if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {
dp[i] += dp[i - 2];
}
}
return dp[n];
}
// 判断字符串编码是否在1到26之间
private static boolean isValidEncoding(String s) {
if (s.charAt(0) == '0') {
return false;
}
int num = Integer.parseInt(s);
return num >= 1 && num <= 26;
}
}
不过可以简化一下,就是比较难理解一点,意义一样滴:
class Solution {
public int numDecodings(String s) {
int n = s.length();
int[] f = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; ++i) {
if (s.charAt(i - 1) != '0') {
f[i] += f[i - 1];
}
if (i > 1 && s.charAt(i - 2) != '0'
&& ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
f[i] += f[i - 2];
}
}
return f[n];
}
}
7 不同路径 II
leetcode 63. 不同路径 II
这题就是62的改版,所以复杂了很多,还是建议看代码随想录:动态规划——不同路径
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
**dp[i] [j] :**表示从(0 ,0)出发,到(i, j) 有dp[i] [j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i] [0]一定为1,dp[0] [j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i] [0]应该还是初始值0。
如图:
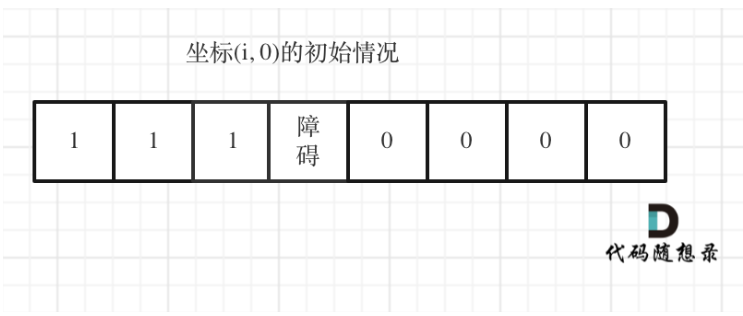
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
int[][] dp = new int[m][n];
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i] [0] == 1的情况就停止dp[i] [0]的赋值1的操作,dp[0] [j]同理
- 确定遍历顺序
从递归公式dp[i] [j] = dp [i - 1] [j] + dp[i] [j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i] [j]的时候,dp[i - 1] [j] 和 dp[i] [j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
- 举例推导dp数组
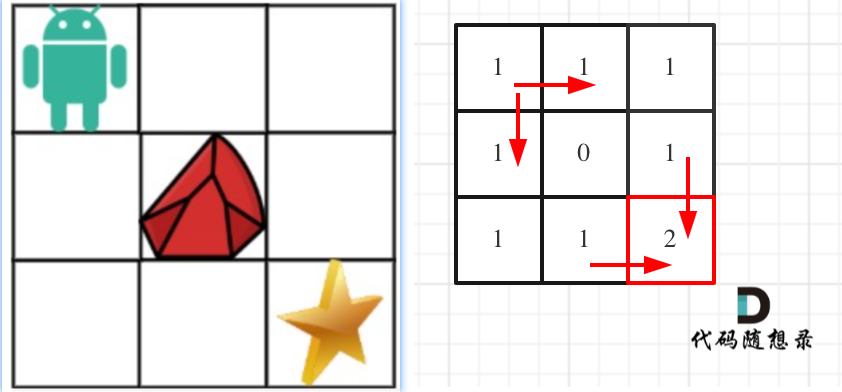
完整代码如下:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
//如果在起点或终点出现了障碍,直接返回0
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
return dp[m - 1][n - 1];
}
}
至于118,119我个人觉得并不合适使用动态规划的方式,所以就不写了,over~~