参考文献:
[1]陈修鹏,李庚银,夏勇.基于主从博弈的新型城镇配电系统产消者竞价策略[J].电力系统自动化,2019,43(14):97-104.
1.基本原理
在竞争性电力市场下,新型城镇配电系统内主要有以下几类主体:电力交易中心和调度部门、产消者、电网公共服务企业以及普通用户。其中,产消者将多余的电能出售给配电网其他用户,每个产消者都是独立且理性的个体,产消者相互之间形成竞争,向交易中心提交竞标曲线,追求自身利益最大化;电网公共服务企业的角色已经发生变化,传统配电网内电网企业从上一级电网购电,是配电网唯一的供电方,而在零售电力市场开放后,电网企业拥有配电经营权,主要提供保底供电服务。一方面,向配电网内售电方收取过网费;另一方面,在配电网内部供电不足时维持功率平衡,保证供电的可靠性,还可以防止配电网内产消者 “抱 团”,故意抬高电价的现象发生。
电力交易中心和调度部门是城镇配电系统零售市场的管理者与监督者,保证系统安全经济运行,引导电力市场有序健康发展。配电网内日前市场具体调度过程如下:产消者在交易日前15日至交易日前1日向交易中心提交竞标曲线,调度中心与交易中心信息透明、相互配合,根据产消者的竞标曲线与用户的用电需求确定各个产消者的调度出力和出清价格。产消者竞价过程与调度过程满足主从递阶结构,可以视为Stackelberg动态博弈过程,本文将该实际问题转化为包含竞价层和调度层的双层优化模型,具体过程如图1所示。

产消者为上层决策者,相当于博弈中的领导者,通过非合作博弈,自主报价,以自身利益最大为优化目标。产消者目标函数的一般数学表达式为:

调度与交易中心为下层决策者,相当于Stackelberg博弈中的跟随者,根据产消者竞标曲线和用电需求,在保证城镇配电系统供电经济性与安全性基础上,以运行成本最低为优化目标,确定各产消者出力。
目标函数的一般数学表达式为:

1.1上层产消者竞价模型
本文考虑的新型城镇配电系统中的产消者i具备微型燃气轮机等常规发电设备,也具备光伏、风电等新能源发电设备。
对于常规发电设备,其发电成本可表示为二次函数,即:

在不完全竞争的电力市场下,产消者将不会按照边际发电成本竞标,而是为提高收益调整竞标曲线。本文基于SFE构造产消者i的竞价函数为:

一般来讲,新能源发电具有随机性和波动性,由于本文旨在研究竞争导致的零售市场均衡问题,故忽略了不确定性因素而采用预测值。在实际调度过程中,由于微型燃气轮机调节速度快,可以平衡新能源发电引起的不平衡量。
调度部门确定产消者调度出力,采用按报价结算(pay as bid, PAB)的收益机制结算,产消者i收益的具体目标为:


1.2下层优化调度模型
本文中电网公共服务企业和普通用户由配电系统调度部门进行统一管理和控制,因此将三者在下层优化调度模型进行论述。
1.2.1 调度部门优化运行模型
新型城镇配电系统优化调度的目标为系统整体运行经济成本最低,包括购电成本、网络损耗成本和DR补偿成本,引入网损成本可以优化潮流分布、降低运行成本,而DR成本是为鼓励实施激励政策而提供的补偿成本。

调度部门在进行调度时应满足如下约束条件。



1.2.2 电网公共服务企业模型

1.2.3普通用户模型
能源互联技术的发展允许配电系统中用户参与DR。DR可以分为电价型DR和激励型DR。采用实时电价(real time price,RTP)结算用户电费可以充分调动用户的DR能力。RTP是一种重要的电价型DR项目,通过价格信号对电网运行和市场运营进行最优引导。

用户通过影响下层调度模型潮流约束中的节点负荷量,进一步影响产消者的调度出力和收益从而参与博弈,防止博弈过程中出现产消者集体垄断导致价格不合理。用户通过参与DR最终减少的用电费用为:

2.主从博弈模型求解过程
2.1产消者竞价主从博弈模型
在城镇配电网中,各产消者是独立的利益主体,调度部门基于产消者竞标曲线安排产消者出力,并确定电网公共服务企业提供的不平衡功率和用户参与需求响应的负荷调整量。而产消者基于调度部门安排的调度出力调整竞价曲线,提高售电收益。产消者与调度部门之间属于完全信息下的Stackelberg动态博弈,产消者之间竞价策略相互影响,属于完全信息下的非合作博弈。最终,各产消者和电网调度部门的博弈可以构建为Nash-Stackelberg博弈模型。通常,博弈包括博弈方、博弈方策略和收益三个因素。

该博弈纳什均衡解的存在性在数学上是难以证明的,但可以对下层调度模型潮流约束条件进行凸松弛,使其转化为二阶锥规划问题,具体过程见附录A第A2节。此时,当产消者竞价策略给定时,下层模型可以确定唯一的优化调度结果,因此每个产消者的最优反应总是存在的,意味着该博弈模型的纳什均衡模型是存在的。
2.2 求解过程
该模型上下层优化目标不一致且变量求解结果相互影响,本文采用改进粒子群优化算法与CPLEX求解器相结合的方法迭代求解模型的均衡解。对于上层产消者非合作博弈模型,采用粒子群优化算法求解迭代过程中产消者的最优竞价策略,该改进粒子群优化算法对粒子位置和速度迭代过程中的权重系数和学习因子重新定义,可实现其自适应调整,提高收敛速度,避免陷入局部最优,改进过程见附录A3。 对于下层优化调度模型,基于YALMIP平 台,采用CPLEX求解器进行求解,以保证解的计算效率和最优性。
具体求解过程如下。

3.编程思路
3.1参数和变量定义
表1 相关参数

表2 上层决策变量

表3 下层决策变量

3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。算例分析用到的大部分数据可以从原文中找到,其他数据可以自己假设一下。然后将所有需要的数据,按照表1的定义格式输入即可。
步骤2:改进粒子群算法
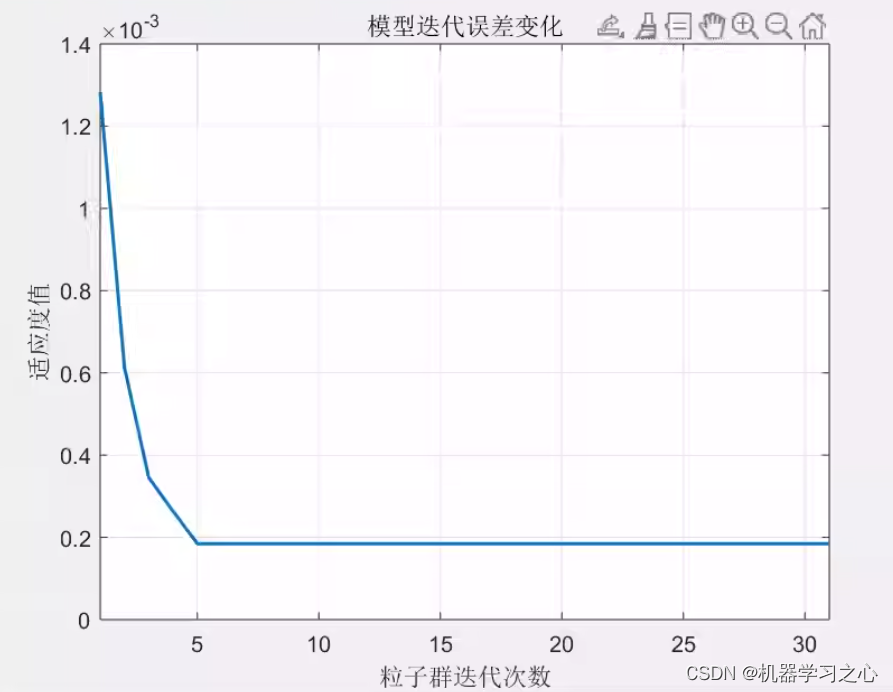
参考文中的改进思路,写出改进粒子群算法的代码。针对Sphere函数,改进粒子群算法和基本粒子群算法的对比如下:
基本粒子群算法:

改进粒子群算法:

说明改进粒子群算法确实效果更好。
步骤3:下层优化调度代码
文章是一个双层博弈问题,为了调试方便,一般都是要先确保下层优化调度问题求解无误,再将其和上层优化结合起来迭代求解。从数学模型上看,下层优化调度就是一个基于混合整数二阶锥规划(MISOCP)的最优潮流问题,和我之前博客(基于混合整数二阶锥(MISOCP)的配电网重构)中模型基本一致,不同之处在于这篇文章中的模型没有拓扑变量(即不考虑重构),且增加了节点电价这一变量。
步骤4:上层粒子群算法
上层粒子群算法中,只有一个决策变量a_G,表示产销者的竞价策略,而产销者的出力策略是通过下层优化调度得到的。上层的目标函数是多个产销者的效益最大化,本质上是一个多目标优化,但文中并没有具体告知是采用怎样的优化方式,我在代码中直接将3个产销者的总体效益最大作为优化目标,将多目标转为单目标。
步骤5:上下层迭代寻优
通过上下层优化迭代求解,得到主从博弈的最优解。
步骤6:输出优化结果
按文中给定的图表形式,求出最终的优化结果。
4.Matlab代码
%% 清除变量
clc
clear
close all
warning off
tic
%% 设置种群参数
parameters;
index = input('选择仿真时刻,1:T=8h,2:T=15h :');
sizepop = 25; % 初始种群个数
dim = 3; % 空间维数
ger = 50; % 最大迭代次数
x_max = f_grid*ones(1,dim); % 位置上限
x_min = zeros(1,dim); % 位置下限
v_max = 20*ones(1,dim); % 速度上限
v_min = -20*ones(1,dim); % 速度下限
wb = 1.5; % 惯性权重初值
we = 0.1; % 惯性权重末值
c_1b = 1.5; % 自我学习因子初值
c_1e = 0.1; % 自我学习因子末值
c_2b = 0.1; % 群体学习因子初值
c_2e = 1.5; % 群体学习因子末值
%% 种群初始化
pop = x_min + rand(sizepop,dim).*(x_max-x_min); % 初始化种群
pop_v = v_min + rand(sizepop,dim).*(v_max-v_min); % 初始化种群速度
pop_zbest = pop(1,:); % 初始化群体最优位置
pop_gbest = pop; % 初始化个体最优位置
fitness = zeros(1,sizepop); % 所有个体的适应度
fitness_zbest = -inf; % 初始化群体最优适应度
fitness_gbest = -inf*ones(1,sizepop); % 初始化个体最优适应度
%% 初始的适应度
for k = 1:sizepop
% 计算适应度值
[Gi,~,~,~,~] = Up_fitnessfun(pop(k,:),index);
fitness(k) = sum(Gi);
if fitness(k) > fitness_zbest
fitness_zbest = fitness(k);
pop_zbest = pop(k,:);
end
end
history_pso = zeros(1,ger); % 粒子群历史最优适应度值
%% 迭代求最优解
iter = 1;
while iter <= ger
% 更新惯性权重和学习因子
g = iter;
g_max = ger;
w = wb - g/g_max*(wb - we);
c_1 = c_1e + (c_1b - c_1e)*(1 - acos(-2*g/g_max + 1)/pi);
c_2 = c_2e + (c_2b - c_2e)*(1 - acos(-2*g/g_max + 1)/pi);
for k = 1:sizepop
% 更新速度并对速度进行边界处理
pop_v(k,:)= w * pop_v(k,:) + c_1*rand*(pop_gbest(k,:) - pop(k,:)) + c_2*rand*(pop_zbest - pop(k,:));
for kk = 1:dim
if pop_v(k,kk) > v_max(kk)
pop_v(k,kk) = v_max(kk);
end
if pop_v(k,kk) < v_min(kk)
pop_v(k,kk) = v_min(kk);
end
end
% 更新位置并对位置进行边界处理
pop(k,:) = pop(k,:) + pop_v(k,:);
for kk = 1:dim
if pop(k,kk) > x_max(kk)
pop(k,kk) = x_max(kk);
end
if pop(k,kk) < x_min(kk)
pop(k,kk) = x_min(kk);
end
end
% 更新适应度值
[Gi,~,~,~,~] = Up_fitnessfun(pop(k,:),index);
fitness(k) = sum(Gi);
if fitness(k) > fitness_zbest
fitness_zbest = fitness(k);
pop_zbest = pop(k,:);
end
if fitness(k) > fitness_gbest(k)
fitness_gbest(k) = fitness(k);
pop_gbest(k,:) = pop(k,:);
end
end
history_pso(iter) = fitness_zbest;
disp(['PSO第',num2str(iter),'次迭代最优适应度=',num2str(fitness_zbest)])
iter = iter+1;
end
time0 = toc;
%% 运行结果
show_result;以上仅为主函数部分的matlab代码,完整的matlab代码可以从这个链接获取:
基于主从博弈的新型城镇配电系统产消者竞价策略matlab代码
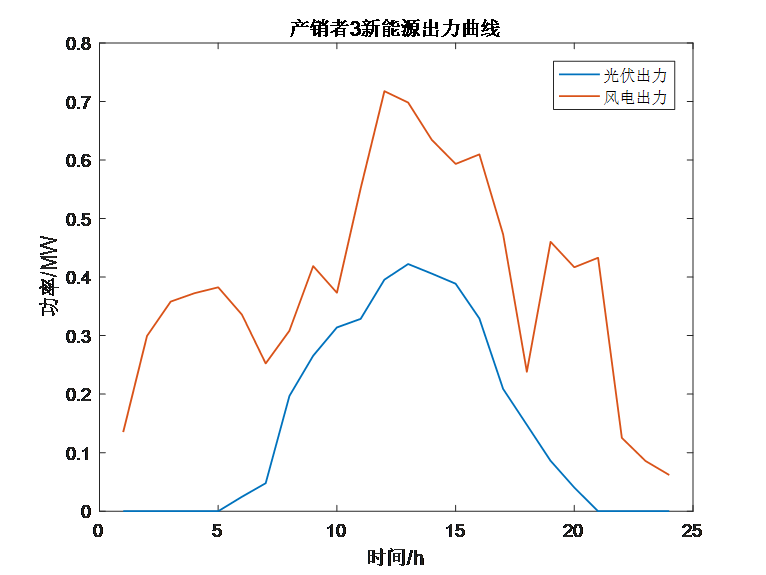
5.运行结果分析
因为原文并未提供完整的数据,因此结果不完全一样,但原理是相同的









![[SUCTF2019]SignIn 题解](https://img-blog.csdnimg.cn/1496bedd7dcb4a2ea7beba2798b40ffc.png)