💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 一、二叉树的概念
- 二、二叉树的特点
- 三、特殊的二叉树
- 1.满二叉树:
- 2.完全二叉树:
- 四、二叉树的存储
- 1.数组存储:
- 2.链式存储
一、二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
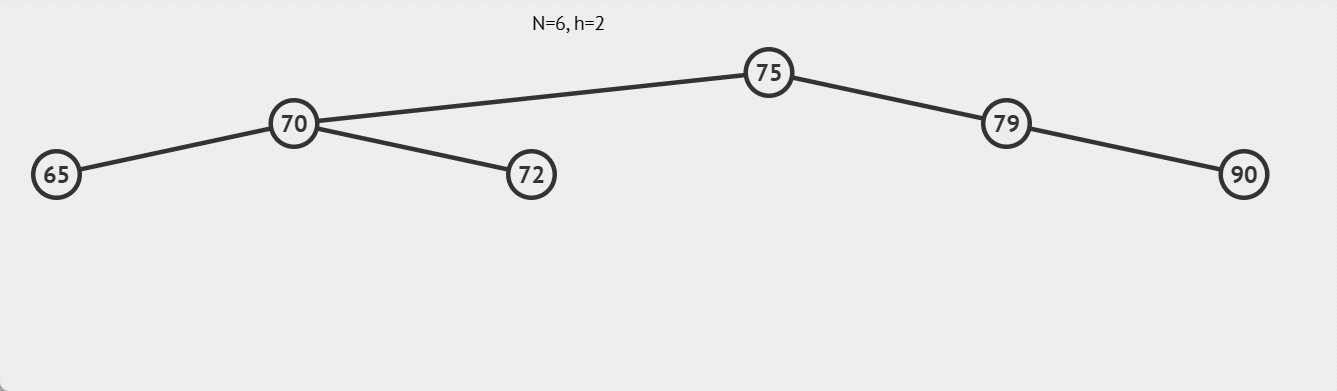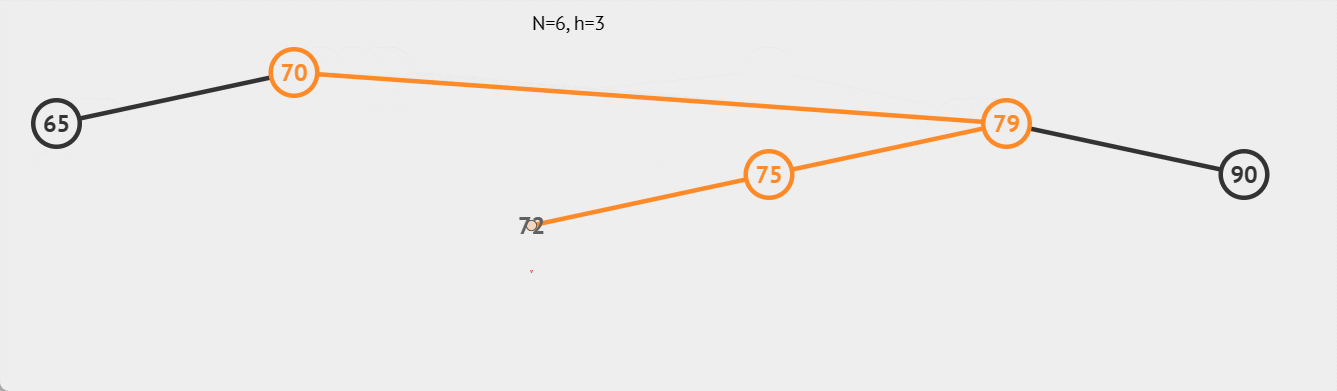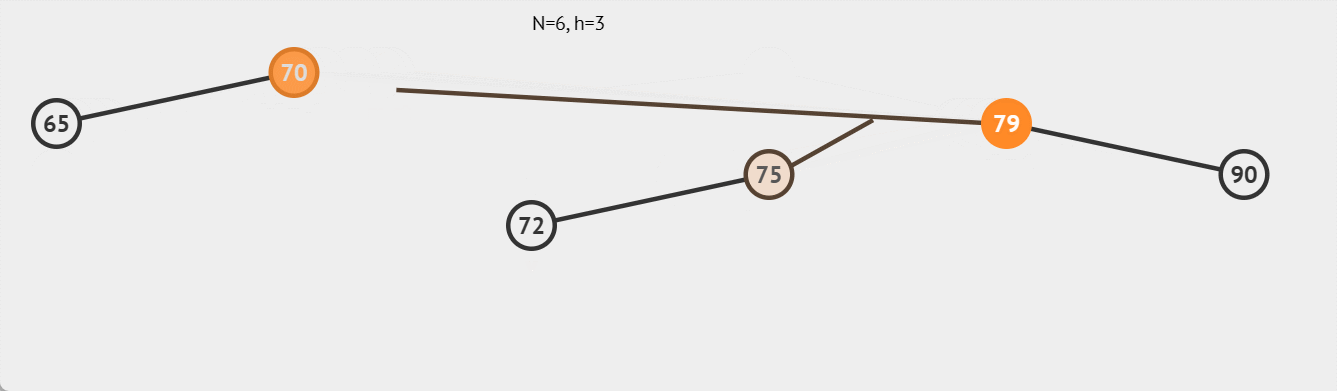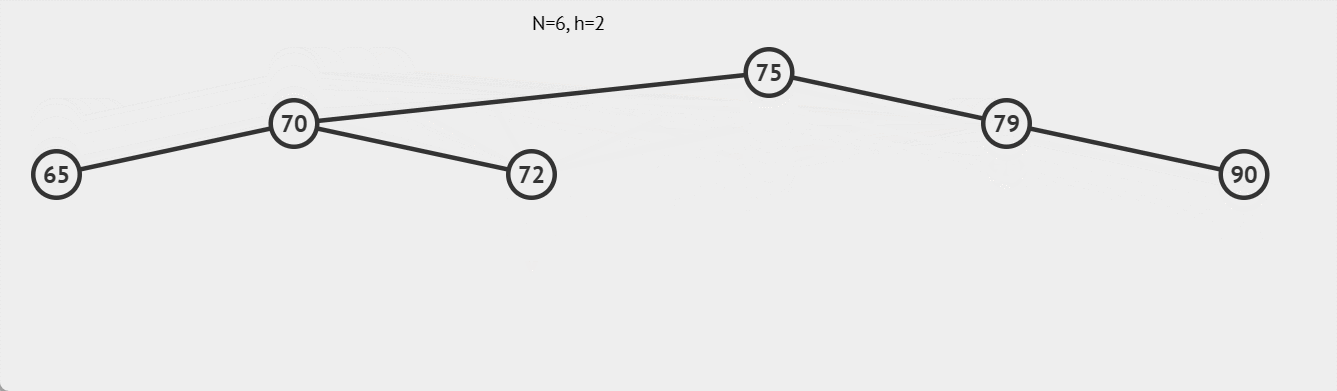
如下图: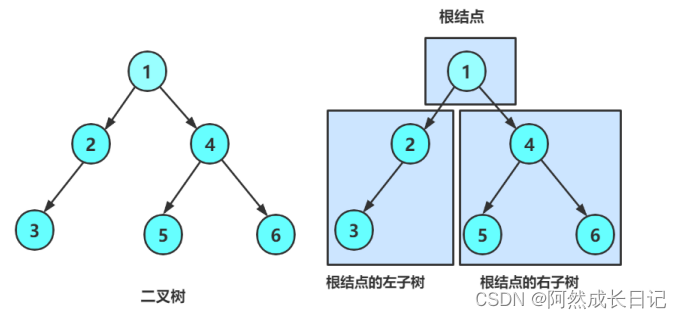
二、二叉树的特点
1.二叉树的度最大为2.即一个节点最多有两个孩子。
2.二叉树可以只有一个根节点,度为0.
3.二叉树的子树有左右之分,是一个有序树。
三、特殊的二叉树
1.满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
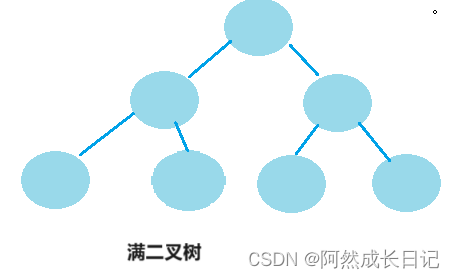
特点:一个H层的满二叉树,其节点数=2^H-1
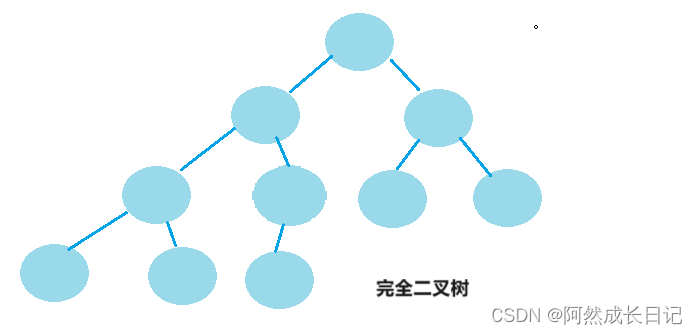
2.完全二叉树:
1.在完全二叉树中,除了最后一层外,所有层的节点数量都是满的,且最后一层的节点都集中在左侧。
2.如果一个结点的索引是 i,则它的左子节点的索引是 2i,右子节点的索引是 2i+1。反之,如果一个节点的索引是 i,则它的父节点的索引是 i/2。
满二叉树是一种特殊的完全二叉树。
特点:
1)相对于其他类型的二叉树,它更容易实现和操作。
2)具有 n 个节点的完全二叉树的高度为 log(n)。
3)在完全二叉树中,除了最后一层可能不满外,其他层都是满的。
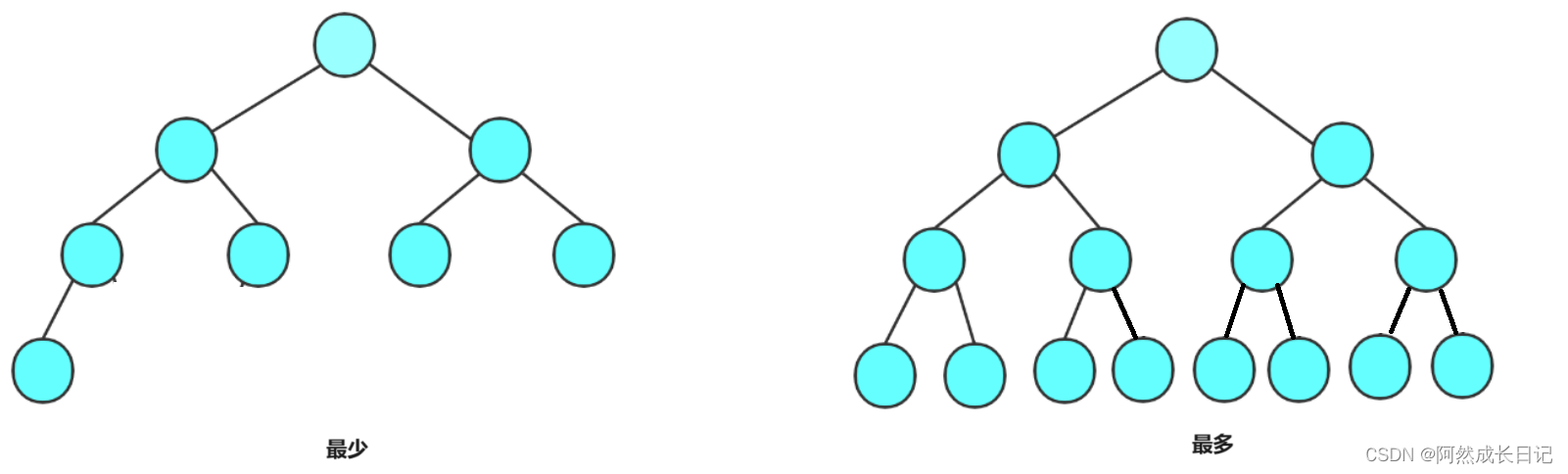
最少:2^(H-1)-1+1 = 2^(H-1)
最多:相当于满二叉树:2^H-1
一个H层的完全二叉树,其节点数范围[2^(H-1)~2^H-1]
四、二叉树的存储
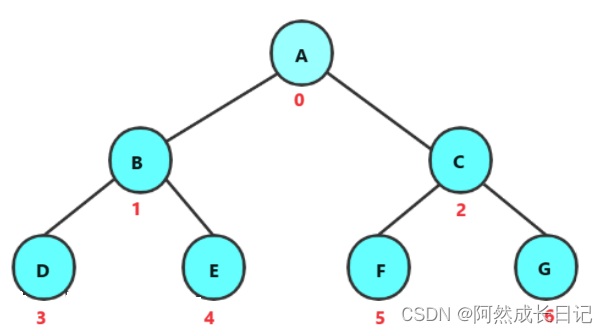
1.数组存储:
这种存储方式适用于完全和满二叉树。还有堆。
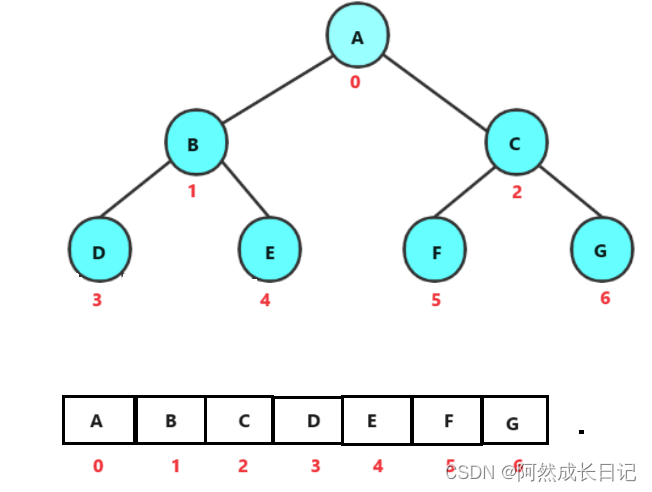
计算:
给定双亲节点,求
左孩子=双亲节点*2+1
右孩子=双亲节点*2+2
给定孩子节点,求
双亲节点=(孩子节点-1)/2
2.链式存储
对于普通二叉树来说,不适合顺序存储方式,因为有可能在补充为完全二叉树过程中,补充太多的0,而浪费大量空间,因此普通二叉树一般使用链式存储。
每一个节点的组成如下图所示
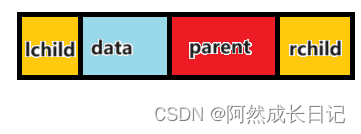
具体结构如下图所示: