Problem - 219D - Codeforces

问题描述：Treeland国有 n 个城市, 这 n 个城市连接成了一棵树, 靠单向道路相连, 现在政府想要选择一个城市作为首都, 条件是首都必须能到达其他所有城市, 现在我们不得不将一些道路反转方向, 记反转的条数为 k 条, 我们要找到所有使 k 最小的首都.

思路：树形dp。找一个根，从根向下遍历，可以求出以u为根的节点到其所有子节点需要反转几次。之后在遍历，求出节点v到它的所有父亲节点需要反转几次。

建树

题目给的是单向边，但是对于反转来说不好处理，可以将其建成双向边。对于<u,v>而言，它的边权是0，<v,u>的边权是1。

    for(int i = 1; i < n; ++i) {
        int u,v; cin>>u>>v;
        g[u].push_back({v,0});
        g[v].push_back({u,1});
    }

dfs1, f1[]

f1[u]表示，以u为根的节点到其所有子节点需要反转的次数。
$$F1[u]=\sum _{v\in u的儿子节点}(F1[v]+w)$$

    auto dfs1 = [&](auto dfs1, int u, int fu) -> void {
        for(auto t: g[u]) {
            int y = t.vf, w = t.vs;
            if(y == fu) continue;
            dfs1(dfs1, y,u);
            f1[u] += f1[y] + w;
        }
    };

dfs2, f2[]

f2[v]表示，以v为根的节点到其所有的父亲节点和和兄弟节点及其子节点需要反转的次数，换言之，就是到除了v的子节点之外的所有节点需要反转的次数。

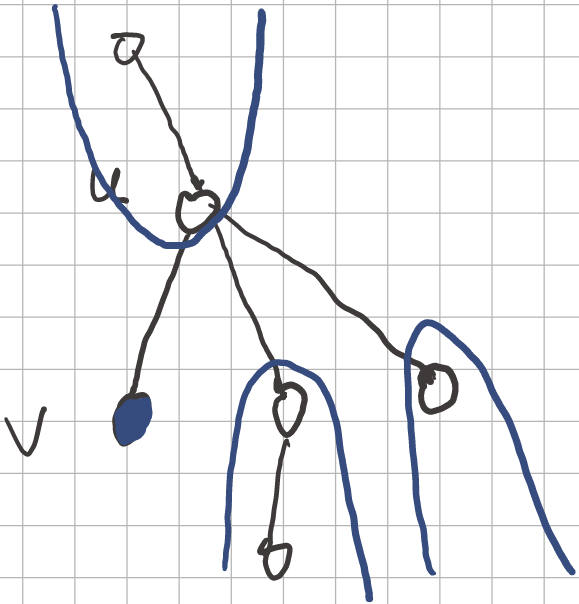
可以发现，到v的祖先的反转次数是f2[u]再加上<v,u>的边权。到其兄弟节点及其兄弟节点的子节点是：u到其儿子节点的反转次数 - v到其儿子节点的反转次数。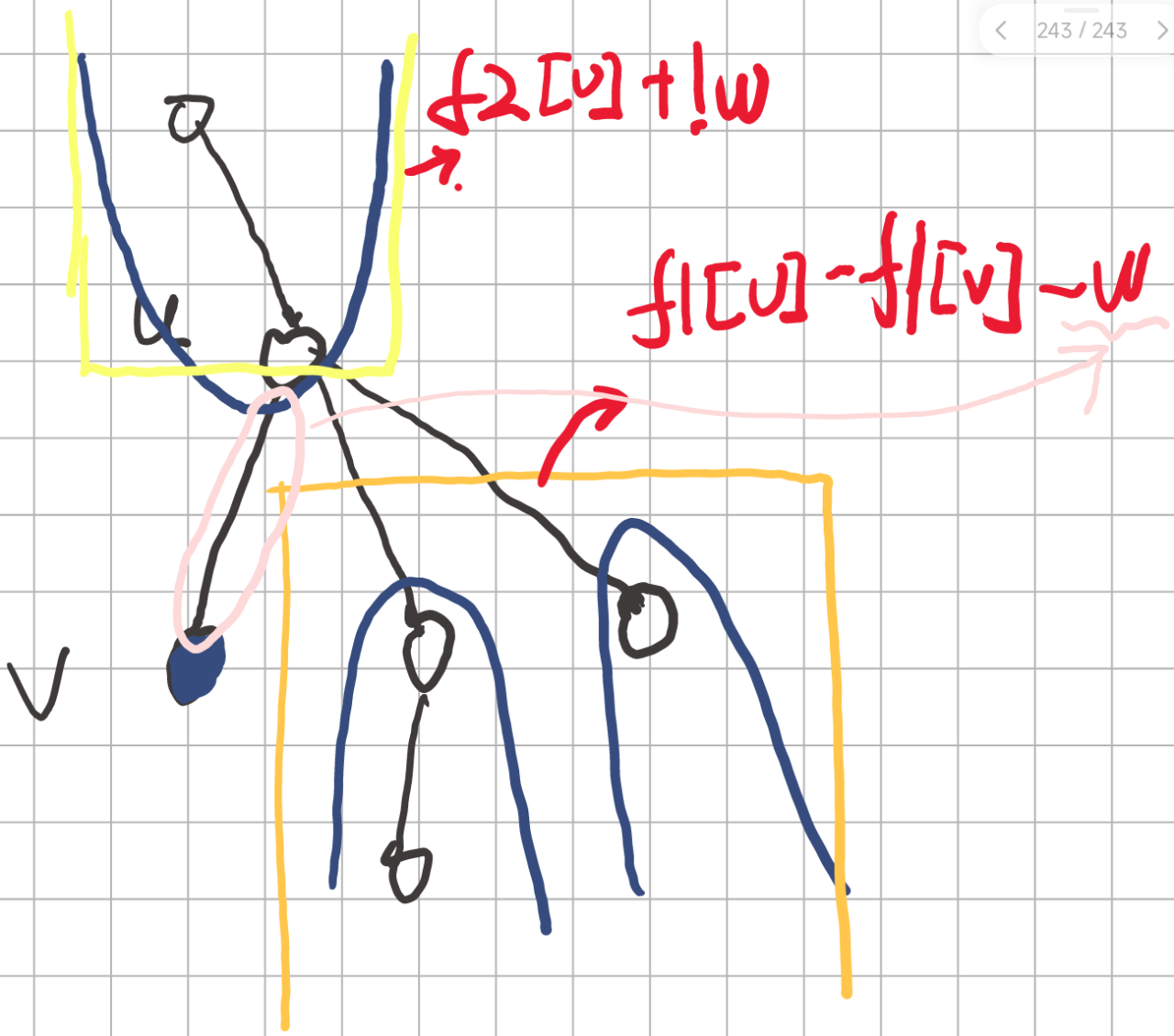
$$F2[v]=F2[u]+!w+F1[u]-F1[v]-w$$

最小反转次数

最小反转次数就是：
$$mi{n}_{v\in 树的节点}(F1[v]+F2[v])$$

代码

void solve() {
    int n; cin>>n;
    vector<vector<PII>> g(n + 1);
    vector<int> f1(n + 1), f2(n + 1);
    for(int i = 1; i < n; ++i) {
        int u,v; cin>>u>>v;
        g[u].push_back({v,0});
        g[v].push_back({u,1});
    }
    auto dfs1 = [&](auto dfs1, int u, int fu) -> void {
        for(auto t: g[u]) {
            int y = t.vf, w = t.vs;
            if(y == fu) continue;
            dfs1(dfs1, y,u);
            f1[u] += f1[y] + w;
        }
    };
    dfs1(dfs1, 1, -1);
    auto dfs2 = [&](auto &&dfs2, int u, int fu) -> void {
        for(auto t: g[u]) {
            int y = t.vf, w = t.vs;
            if(y == fu) continue;
            f2[y] = f2[u] + !w + f1[u] - f1[y] - w;
            dfs2(dfs2, y,u);
        }
    };
    dfs2(dfs2,1,-1);
    int mi = INF;
    for(int i = 1; i <= n; ++i) mi = min(f1[i] + f2[i], mi);
    cout<<mi<<endl;
    for(int i = 1; i <= n; ++i) {
        if(mi == f1[i] + f2[i]) {
            cout<<i<<" ";
            // return ;
        }
    }
}

https://zhuanlan.zhihu.com/p/568881717