【2023高教社杯】A题 定日镜场的优化设计 问题分析及数学模型

1 题目
构建以新能源为主体的新型电力系统,是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。
定日镜是塔式太阳能光热发电站(以下简称塔式电站)收集太阳能的基本组件,其底座由纵向转轴和水平转轴组成,平面反射镜安装在水平转轴上。纵向转轴的轴线与地面垂直,可以控制反射镜的方位角。水平转轴的轴线与地面平行,可以控制反射镜的俯仰角,定日镜及底座示意图见图 1。两转轴的交点(也是定日镜中心)离地面的高度称为定日镜的安装高度。塔式电站利用大量的定日镜组成阵列,称为定日镜场。定日镜将太阳光反射汇聚到安装在镜场中吸收塔顶端上的集热器,加热其中的导热介质,并将太阳能以热能形式储存起来,再经过热交换实现由热能向电能的转化。太阳光并非平行光线, 而是具有一定锥形角的一束锥形光线,因此太阳入射光线经定日镜任意一点的反射光线也是一束锥形光线[2]。定日镜在工作时,控制系统根据太阳的位置实时控制定日镜的法向,使得太阳中心点发出的光线经定日镜中心反射后指向集热器中心。集热器中心的离地高度称为吸收塔高度。

图 1 定日镜及底座示意图
现计划在中心位于东经 98.5∘,北纬 39.4∘,海拔 3000 m,半径 350 m 的圆形区域内建设一个圆形定日镜场(图 2)。

图 2 圆形定日镜场示意图(金台资讯,2021-11-22)
以圆形区域中心为原点,正东方向为 𝑥 轴正向,正北方向为 𝑦 轴正向,垂直于地面向上方向为 z 轴正向建立坐标系,称为镜场坐标系。规划的吸收塔高度为 80 m,集热器采用高 8 m、直径 7 m 的圆柱形外表受光式集热器。吸收塔周围 100 m 范围内不安装定日镜,留出空地建造厂房,用于安装发电、储能、控制等设备。定日镜的形状为平面矩形,其上下两条边始终平行于地面,这两条边之间的距离称为镜面高度, 镜面左右两条边之间的距离称为镜面宽度,通常镜面宽度不小于镜面高度。镜面边长在 2 m 至8 m 之间,安装高度在 2 m 至 6 m 之间,安装高度必须保证镜面在绕水平转轴旋转时不会触及地面。由于维护及清洗车辆行驶的需要,要求相邻定日镜底座中心之间的距离比镜面宽度多 5m以上。为简化计算,本问题中所有“年均”指标的计算时点均为当地时间每月 21 日 9:00、10:30、12:00、13:30、15:00。请建立模型解决以下问题:
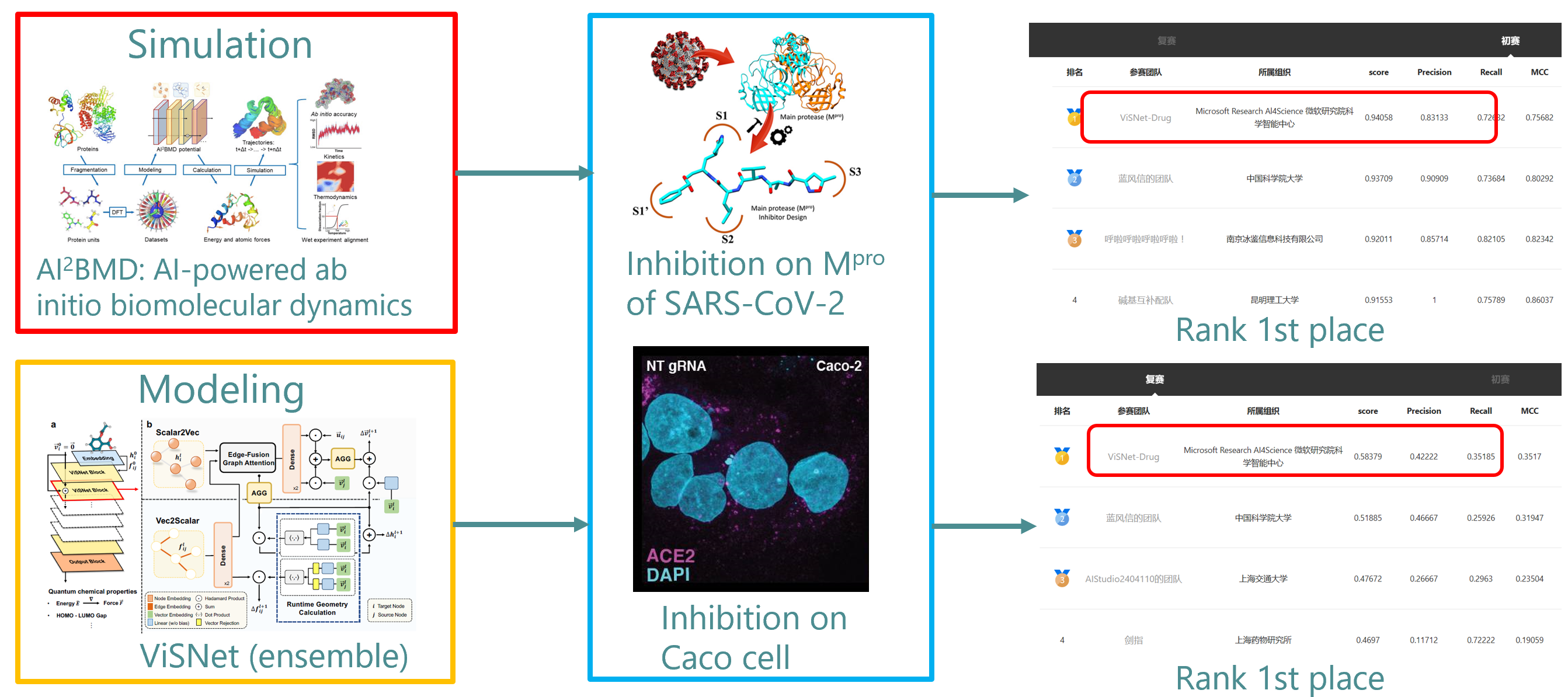
问题 1 若将吸收塔建于该圆形定日镜场中心,定日镜尺寸均为 6 m×6 m,安装高度均为4 m,且给定所有定日镜中心的位置(以下简称为定日镜位置,相关数据见附件),请计算该定日镜场的年平均光学效率、年平均输出热功率,以及单位镜面面积年平均输出热功率(光学效率及输出热功率的定义见附录)。请将结果分别按表 1 和表 2 的格式填入格。
问题 2 按设计要求,定日镜场的额定年平均输出热功率(以下简称额定功率)为 60 MW。若所有定日镜尺寸及安装高度相同,请设计定日镜场的以下参数:吸收塔的位置坐标、定日镜尺寸、安装高度、定日镜数目、定日镜位置,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。请将结果分别按表 1、2、3 的格式填入表格,并将吸收塔的位置坐标、定日镜尺寸、安装高度、位置坐标按模板规定的格式保存到 result2.xlsx 文件中。
问题 3 如果定日镜尺寸可以不同,安装高度也可以不同,额定功率设置同问题 2,请重新设计定日镜场的各个参数,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。请将结果分别按表 1、表 2 和表 3 的格式填入表格,并将吸收塔的位置坐标、各定日镜尺寸、安装高度、位置坐标按模板规定的格式保存到result3.xlsx 文件中。
表1 问题X每月21日平均光学效率及输出功率
| 日期 | 平均 光学效率 | 平均 余弦效率 | 平均阴影遮挡效率 | 平均 截断效率 | 单位面积镜面平均输出热功率 (kW/m2) |
|---|---|---|---|---|---|
| 1 月 21 日 | |||||
| 2 月 21 日 | |||||
| 3 月 21 日 | |||||
| 4 月 21 日 | |||||
| 5 月 21 日 | |||||
| 6 月 21 日 | |||||
| 7 月 21 日 | |||||
| 8 月 21 日 | |||||
| 9 月 21 日 | |||||
| 10 月 21 日 | |||||
| 11 月 21 日 | |||||
| 12 月 21 日 |
表2 问题X年平均光学效率及输出功率表
| 年平均光学效率 | 年平均余弦效率 | 年平均阴影遮挡效率 | 年平均截断效率 | 年平均输出热功率 (MW) | 单位面积镜面年平均输出热功率 (kW/m2) |
|---|---|---|---|---|---|
表3 问题 X设计参数表
| 吸收塔位置坐标 | 定日镜尺寸(宽 × 高) | 定日镜安装高度(m) | 定日镜总面数 | 定日镜总面积 |
|---|---|---|---|---|
注 在表 3 中填入问题 3 的结果时,“定日镜尺寸”及“定日镜安装高度”两栏可空缺
2 问题分析
2.0 符号说明
| 符号 | 意义 |
|---|---|
| φ \varphi φ | 圆形定日镜场中心的纬度(北纬) |
| α s \alpha_s αs | 太阳高度角 |
| γ s \gamma_s γs | 太阳方位角 |
| ω \omega ω | 太阳时角, ω = π 12 ( S T − 12 ) \omega =\frac{\pi}{12}(ST-12) ω=12π(ST−12) |
| S T ST ST | 当地标准时间,单位为小时 |
| δ \delta δ | 太阳赤纬角 |
| D D D | 以春分作为第0天起算的天数 |
| H H H | 地面高度,单位为km |
| G 0 G_0 G0 | 太阳常数,其值取为1.366kW/m^2 |
| a a a、 b b b、 c c c | 大气折射系数的常用参数 |
| D N I DNI DNI | 法向直接辐射辐照度,单位为 kW/m^2 |
| E f i e l d E_{field} Efield | 定日镜长的输出热功率,单位为 kW |
| η i \eta_i ηi | 第 i i i面镜子的光学效率 |
| N N N | 定日镜总数(单位:面) |
| A i A_i Ai | 第i面定日镜采光面积(单位:m^2) |
| η s b \eta_{sb} ηsb、 η c o s \eta_{cos} ηcos、 η a t \eta_{at} ηat、 η t r u n c \eta_{trunc} ηtrunc、 η r e f \eta_{ref} ηref | 定日镜的光学效率中的五个效率参数 |
| η \eta η | 定日镜的光学效率, η = η s b ⋅ η c o s ⋅ η a t ⋅ η t r u n c ⋅ η r e f \eta=\eta_{sb}\cdot\eta_{cos}\cdot\eta_{at}\cdot\eta_{trunc}\cdot\eta_{ref} η=ηsb⋅ηcos⋅ηat⋅ηtrunc⋅ηref |
2.1 问题一
首先,建立定日镜场的坐标系,以圆形区域中心为原点,正东方向为x轴正向,正北方向为y轴正向,垂直于地面向上方向为z轴正向。根据给定的定日镜数据,将每个定日镜的位置坐标转换到镜场坐标系中。
(1)计算每个定日镜底座中心点的坐标,以及该点的纬度、经度和安装高度。
(2)根据公式计算出每个定日镜在每个计算时点的太阳高度角、太阳方位角和法向直接辐射辐照度,以及求出该时点的集热器中心坐标。
(3)计算每个定日镜在每个计算时点的各个光学损失的效率,以及集热器截断效率和镜面发射率。进而求出各个定日镜的光学效率。
(4)计算每个定日镜的输出热功率;所有定日镜的总输出热功率即为该定日镜场的总输出热功率。
(5)根据输出功率和镜面面积,计算单位面积镜面年平均输出热功率。
(6)求出每个计算时点的平均光学效率、平均余弦效率、平均阴影遮挡效率、平均截断效率和单位面积镜面平均输出热功率。并计算年平均光学效率、年平均余弦效率、年平均阴影遮挡效率、年平均截断效率和年平均输出热功率以及单位面积镜面年平均输出热功率。
2.2 问题二
这是最优化问题。首先在问题一中已经求出了:太阳高度角、太阳方位角、定日镜的投影面积、定日镜的采光面积、定日镜的年平均输出热功率。根据题目需要求解吸收塔的位置坐标、定日镜的尺寸、安装高度以及定日镜的数目和位置坐标,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。则以吸收塔为中心,枚举定日镜位置,选择面积最小的定日镜作为基准定日镜,计算该定日镜在所有时刻的输出热功率。输出单位镜面面积年平均输出热功率时的参数。
(1)先假设定日镜的尺寸和安装高度已知,需要求解每个定日镜的位置和定日镜的数目。
(2)尝试在不同的定日镜密度下,计算定日镜场的单位镜面面积年平均输出热功率,找出最优解。
(3)约束条件如下
-
镜面高度<安装高度−80m<安装高度−80m
-
镜面宽度>镜面高度>镜面高度
-
镜面边长在2m至8m之间
-
安装高度在2m至6m之间
2.3 问题三
根据题目要求,需要改进的模型包括定日镜尺寸和安装高度。需要考虑如何合理选择定日镜尺寸和安装高度以最大限度地发电,同时满足额定功率要求。改进两个点:
(1)定日镜尺寸的选择:可以通过对不同尺寸的定日镜进行效率和能量收集能力的评估,选择效率高且能够收集到更多太阳能的定日镜尺寸。可以通过实验或者模拟计算来确定最佳的定日镜尺寸。
(2)安装高度的选择:可以考虑将光伏阵列安装在可调整安装高度的机架上,以便实现最佳的太阳能接收效果。通过模拟不同安装高度下的太阳能收集情况,选择能够最大限度地收集到太阳能的安装高度。
3 数学模型
3.1 问题一
设定日镜的总数量为 N N N,其中第 i i i个定日镜的坐标为 ( x i , y i , h i ) (x_i, y_i, h_i) (xi,yi,hi),直径为 d i d_i di,安装高度为 h i h_i hi;吸收塔的位置为 ( x 0 , y 0 , h 0 ) (x_0, y_0, h_0) (x0,y0,h0),高度为 H H H。
(1)计算太阳高度角和方位角:
设当地时间为 t t t,月份为 m m m,则可计算出 ω \omega ω和 δ \delta δ。将 ω \omega ω和 h h h代入公式计算出太阳高度角 α s \alpha_s αs和方位角 γ s \gamma_s γs。
ω = π 12 ⋅ ( t − 12 ) \omega = \frac{\pi}{12}\cdot (t-12) ω=12π⋅(t−12)
δ = sin − 1 [ sin ( 2 π D 365 ) ⋅ sin ( 2 π 365 ⋅ 23.45 ) ] \delta = \sin^{-1} \left[\sin\left(\frac{2\pi D}{365}\right) \cdot \sin \left(\frac{2\pi}{365} \cdot 23.45 \right) \right] δ=sin−1[sin(3652πD)⋅sin(3652π⋅23.45)]
α s = sin − 1 [ cos δ ⋅ cos φ ⋅ cos ω + sin δ ⋅ sin φ ] \alpha_s = \sin^{-1}\left[\cos \delta \cdot \cos \varphi \cdot \cos \omega + \sin \delta \cdot \sin \varphi \right] αs=sin−1[cosδ⋅cosφ⋅cosω+sinδ⋅sinφ]
γ s = { cos − 1 [ sin δ − sin α s ⋅ sin φ cos α s ⋅ cos φ ] 当 sin ω > 0 2 π − cos − 1 [ sin δ − sin α s ⋅ sin φ cos α s ⋅ cos φ ] 当 sin ω ≤ 0 \gamma_s = \begin{cases} \cos^{-1}\left[\frac{\sin \delta - \sin \alpha_s \cdot \sin \varphi}{\cos \alpha_s \cdot \cos \varphi}\right] & \text{当}\sin \omega > 0 \\ 2\pi-\cos^{-1}\left[\frac{\sin \delta - \sin \alpha_s \cdot \sin \varphi}{\cos \alpha_s \cdot \cos \varphi}\right] & \text{当}\sin \omega \leq 0 \\ \end{cases} γs=⎩ ⎨ ⎧cos−1[cosαs⋅cosφsinδ−sinαs⋅sinφ]2π−cos−1[cosαs⋅cosφsinδ−sinαs⋅sinφ]当sinω>0当sinω≤0
(2)计算法向直接辐射辐照度:
D N I = G 0 [ a + n exp ( − c sin α s ) ] DNI=G_0[a+n\exp{\left (-\frac{c}{\sin\alpha_s}\right )}] DNI=G0[a+nexp(−sinαsc)]
其中 a = 0.4237 − 0.00821 ( 6 − H ) 2 a =0.4237-0.00821(6-H)^2 a=0.4237−0.00821(6−H)2, b = 0.5505 + 0.00595 ( 6.05 − H ) 2 b =0.5505+0.00595(6.05-H)^2 b=0.5505+0.00595(6.05−H)2, c = 0.2711 + 0.01858 ( 2.5 − H ) 2 c =0.2711+0.01858(2.5-H)^2 c=0.2711+0.01858(2.5−H)2, G 0 G0 G0是太阳常数1.366kW/m^2, n n n是大气遮挡因子,在本模型中取为1。
(3)计算单面定日镜的输出热功率:
E f i e l d = D N I ⋅ A i ⋅ η i E_{field}=DNI\cdot A_i \cdot \eta_i Efield=DNI⋅Ai⋅ηi
其中 A i A_i Ai是单面定日镜的采光面积, η i \eta_i ηi是单面定日镜的光学效率。
(4)计算光学效率:
η = η s b ⋅ η c o s ⋅ η a t ⋅ η t r u n c ⋅ η r e f \eta = \eta_{sb} \cdot \eta_{cos} \cdot \eta_{at} \cdot \eta_{trunc} \cdot \eta_{ref} η=ηsb⋅ηcos⋅ηat⋅ηtrunc⋅ηref
其中,阴影遮挡效率 η s b \eta_{sb} ηsb和余弦效率 η c o s \eta_{cos} ηcos可以用太阳方位角和太阳高度角的值计算;大气透射率 η a t \eta_{at} ηat可以用海拔高度计算;集热器截断效率 η t r u n c \eta_{trunc} ηtrunc和镜面发射率 η r e f \eta_{ref} ηref取为常数。
阴影遮挡效率:
η s b = A sun A i \eta_{sb} = \frac{A_{\text{sun}}}{A_i} ηsb=AiAsun
其中 A sun A_{\text{sun}} Asun表示太阳盘面在定日镜上的投影面积。当劈面向太阳的部分面积覆盖太阳盘面时, A sun = 0 A_{\text{sun}}=0 Asun=0;当太阳盘面全部投影在定日镜表面时, A sun = A i A_{\text{sun}}=A_i Asun=Ai;否则, A sun A_{\text{sun}} Asun可以用几何法计算得到。
余弦效率:
η c o s = cos α s cos θ s \eta_{cos}=\frac{\cos \alpha_s}{\cos\theta_s} ηcos=cosθscosαs
其中 θ s \theta_s θs表示定日镜的俯仰角,可以用定日镜位置和集热器位置的坐标计算得到。
大气透射率:
η a t = { 0.99321 − 0.0001176 d H R + 1.97 × 1 0 − 8 × d H R 2 当 d H R ≤ 1000 0.75 当 d H R > 1000 \eta_{at} = \begin{cases} 0.99321-0.0001176 d_{HR}+1.97 ×10^{-8}×d_{HR}^2 & \text{当}d_{HR} \leq 1000 \\ 0.75 & \text{当} d_{HR} >1000 \\ \end{cases} ηat={0.99321−0.0001176dHR+1.97×10−8×dHR20.75当dHR≤1000当dHR>1000
其中, d H R d_{HR} dHR表示镜面中心到集热器中心的距离,单位是米。
集热器截断效率:
η t r u n c = A sun A t o t a l \eta_{trunc} = \frac{A_{\text{sun}}}{A_{total}} ηtrunc=AtotalAsun
其中 A t o t a l A_{total} Atotal表示单面定日镜的采光面积与集热器表面积之和。
镜面发射率:
η r e f = 0.92 \eta_{ref}=0.92 ηref=0.92
(5)计算单位面积镜面年平均输出热功率、总输出热功率和年平均光学效率:
单位面积镜面年平均输出热功率:
E ‾ f i e l d = ∑ i = 1 N E f i e l d , i N ⋅ f year \overline{E}_{field}=\frac{\sum_{i=1}^N E_{field,i}}{N} \cdot f_{\text{year}} Efield=N∑i=1NEfield,i⋅fyear
其中 f year f_{\text{year}} fyear为一年中的计算时点个数,本题中为5个。
总输出热功率:
E f i e l d t o t a l = ∑ i = 1 N E f i e l d , i ⋅ f year ⋅ A i E_{field}^{total}=\sum_{i=1}^N E_{field,i} \cdot f_{\text{year}}\cdot A_i Efieldtotal=i=1∑NEfield,i⋅fyear⋅Ai
年平均光学效率:
η ‾ = ∑ i = 1 N η i N ⋅ f year \overline{\eta}=\frac{\sum_{i=1}^N \eta_i}{N} \cdot f_{\text{year}} η=N∑i=1Nηi⋅fyear
(6)计算每个计算时点的平均光学效率、平均余弦效率、平均阴影遮挡效率、平均截断效率和单位面积镜面平均输出热功率,以及年平均光学效率、年平均余弦效率、年平均阴影遮挡效率、年平均截断效率和年平均输出热功率以及单位面积镜面年平均输出热功率。
3.2 问题二
(1)模型假设
-
忽略地形对太阳高度角和方位角的影响;
-
假设每个定日镜的安装高度、尺寸和镜面朝向均相同;
-
忽略定日镜与吸收塔之间的阴影遮挡;
-
忽略大气折射和散射对太阳辐照度的影响;
-
定日镜全天处于正对太阳的状态。
(2)参数定义
- x i , y i x_i, y_i xi,yi: 第 i i i面定日镜底座中心的 x x x坐标和 y y y坐标
- N N N: 定日镜数量
- s s s: 定日镜的边长
- h h h: 定日镜的安装高度
(3)目标函数
请下载完整资料
3.3 问题三
假设有n种不同尺寸的定日镜可供选择,其中第i种定日镜的尺寸为 s i s_i si ( i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n)。假设有m个不同安装高度可供选择,其中第j个安装高度为 h j h_j hj ( j = 1 , 2 , . . . , m j=1,2,...,m j=1,2,...,m)。
可以定义变量:
- P i j P_{ij} Pij: 使用第i种尺寸的定日镜,在第j个安装高度下的发电量
- c i j c_{ij} cij: 使用第i种尺寸的定日镜,在第j个安装高度下的定日镜成本
- E i j E_{ij} Eij: 使用第i种尺寸的定日镜,在第j个安装高度下的能源收集效率
则目标是选择合适的定日镜尺寸和安装高度,使得累计发电量最大,并且满足额定功率要求。可以建立如下数学模型:
请下载完整资料
4 完整资料