《算法竞赛·快冲300题》将于2024年出版，是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码，以中低档题为主，适合入门、进阶。

“ 附近的牛” ，链接： http://oj.ecustacm.cn/problem.php?id=1897

题目描述

【题目描述】 农场由 N 个点和 N-1 条双向路径组成。通过 N-1 条路径使得所有点连通。
点 i 有 C(i) 头奶牛，奶牛有时会穿过 K 条路径移动到不同的点。
农夫想要在每个点 i 种植足够的草来喂养最大数量的奶牛 M(i)。
也就是说，对于每个点 i ，农夫需要考虑最多可能会有多少头奶牛到达该点 i 。
请求出每个 M(i)。
【输入格式】 第 1 行：两个整数， N 和 K，1 <= N <= 100,000，1 <= K <= 20。
第 2 行 - 第 N 行：两个整数 u 和 v ，表示点 u 和点 v 之间存在路径，1 <= u, v <= N。
第 N + 1 行 - 第 2N 行：第 N + i 行输入 1 个整数表示 C(i)，0 <= C(i) <= 1000。
【输出格式】 输出 N 行，第 i 行输出 M(i)。
【输入样例】

6 2
5 1
3 6
2 4
2 1
3 2
1
2
3
4
5
6

【输出样例】

15
21
16
10
8
11

---

题解

   简单概况题意：一棵有n个点、n-1条边的树，每个点有权值，对每个节点求出距离它不超过k的所有节点权值之和m。
   先考虑暴力法。对任意一个点i，直接遍历距离它不超过k的所有点，求它的权值之和mi。编码用dfs，从每个点dfs，深度为k时返回。计算量有多大？假设这棵树是一棵满二叉树，从一个点出发走k步，可能走到$2^k$个点，当k=20时，$2^{20}>100000$，已经包括了所有的n个点。所以单独求一个点的m是O(n)的，求n个点的m是$O(n^2)$的，超时。
   如何优化？对每个点单独计算m，导致了大量的重复计算。例如相邻的两个点u、v，点u的距离k之内的点，和点v的距离k之内的点，绝大部分是重复的，只需要计算那些不同的点即可。
   所以本题的思路和编码步骤是：（1）首先计算以任意点i为根的子树的权值之和si，做一次DFS即可；（2）再计算从任意点i出发的权值之和mi，它包括了i的子树权值之和si，以及i的父节点方向的权值，这个计算利用了前面的结果。
   （1）计算任意点i的子树的权值之和。
   设状态为dp[][]，dp[i][j]表示以第i个节点为根的子树上，从i走j步到达的子节点的权值之和。注意不是从i出发的距离j步之内的权值之和，而是距离为j步的那些子节点的权值之和。代码用dfs1()函数做一次DFS，即可计算出每个点的dp[][]。
   注意，dp[][]在以下的计算中有新的含义：dp[i][j]表示从i出发，走j步到达的节点的权值之和。不仅仅包括i的子树上的第j步节点，而且包括父节点方向的第j步的节点。
   （2）计算点v的距离k内的所有节点权值之和m，见下图。

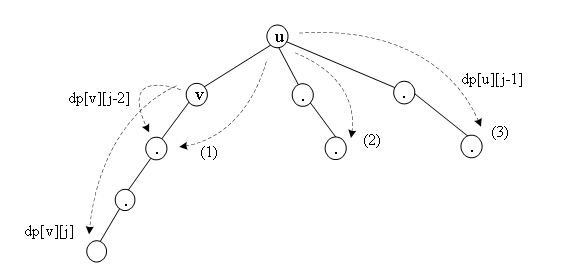
   包括两部分：
   1）v向下走的子树上的节点，这部分权值等于之前在dfs1()算出的dp[v][j]，0≤j≤k。
   2）v向上走的距离k内的节点，这部分权值之和怎么算？v往上走一步是父节点u，u对应的dp[u][j-1]，是u的距离第k-1步的那些节点的权值之和，它包括图中虚线(1)、(2)、(3)的箭头终点上的几个节点权值之和。计算v在u方向的权值之和时，应该加上(2)、(3)，不要加(1)，也就是从dp[u][j-1]中去掉dp[v][j-2]，即dp[u][j-1] - dp[v][j-2]。
   代码dfs2()函数中，用tot[]记录答案，tot[u]是第u点的距离k内的权值之和。dfs2()中的dp[u][i]已经更新为新含义，第20行累加dp[u][i]，0≤j≤k，即可计算出tot[u]。
   第21-26行计算并更新dp[][]为新含义下的权值之和。注意不要忘记更新dp[v][1]，在第24行加上v的父节点u的权值dp[u][0]。
   dfs2()有两个关键。
   1）第23行j从k到2，倒过来循环。dp[v][j] += dp[u][j - 1] - dp[v][j - 2]，左边的dp[][]是新含义，右边的dp[][]是dfs1()计算时的旧含义，j倒过来循环能避免破坏这个关系。
   2）第25行在最后继续dfs2()，也就是在前面更新dp[][]之后再继续DFS。首次进入dfs2()时，u是整棵树的根节点1，它没有父节点，计算tot[1]直接累加dp[u][i]即可。后面继续计算子节点的tot[]时，需要按上图的说明，计算两个部分的权值。
   dfs1()和dfs1()的计算复杂度都是O(n)。

【重点】 树形DP 。

C++代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int K = 22;
int n, k;
int c[N];
vector<int> e[N];                   //存图
int dp[N][K];
void dfs1(int u, int fa) {          //dp[i][j]:i往子树走j步，第j步子节点权值之和
    dp[u][0] = c[u];                //先加上自己的权值
    for(auto v : e[u]){
        if(v == fa) continue;
        dfs1(v, u);                 //注意：先dfs，计算出子节点的dp[][]，回溯后带回
        for(int j=1; j<=k; j++)     //从第j=1步开始，一步一步往下走并计算
            dp[u][j] += dp[v][j - 1];
    }
}
int tot[N];
void dfs2(int u, int fa) {
    for(int i=0; i<=k; i++)  tot[u] += dp[u][i]; //第 1)部分：先累加u子树上，k步内的权值之和        
    for(auto v : e[u]){                          //第 2)部分：然后计算u的子节点的权值之和
        if(v == fa) continue;
        for(int j=k; j>=2; j--)  dp[v][j] += dp[u][j - 1] - dp[v][j - 2];
        dp[v][1] += dp[u][0];                    //v往父节点u走一步，加上u的权值
        dfs2(v, u);
    }
}
int main(){
    cin>>n>>k;
    for(int i=1; i<n; i++) {
        int u, v; scanf("%d%d", &u, &v);
        e[u].push_back(v);
        e[v].push_back(u);
    }
    for(int i=1; i<=n; i++)  scanf("%d", &c[i]);
    dfs1(1, 1);     //以1为根，求每个点往子节点方向走k步的m值
    dfs2(1, 1);     //仍然从根1出发，求每个点的权值之和
    for(int i=1; i<=n; i++)  printf("%d\n", tot[i]);
    return 0;
}

Java代码

Python代码