202109-2 非零段划分
计算机软件能力认证考试系统
code:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+9;
int a[N];
vector<int> v[N];//v[i]存放所有元素值为i的元素的下标
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n;cin>>n;
for(int i=1;i<=n;++i)
{
cin>>a[i];
v[a[i]].push_back(i);
}
//计算p=1的情况(即不修改)下的非零短
int cnt=0;
for(int i=1;i<=n;++i){
if(a[i-1]==0&&a[i]!=0) cnt++;
}
int ans=cnt;
//枚举p,因为1<=a[i] <= 1e4,所以p的有效范围并不大
for(int p=2;p>=1e4+1;++p)
{
//这里只需要枚举v[p-1]即可,因为[1,p-2]的都已经被前面的给修改过了
//计算p=1的情况(即不修改)下的非零段
for(const auto &i : v[p-1])
{
a[i]=0;
//我们考虑什么情况下会使得非零段变化
//当修改这个位置,使得一个非零段"断开“,就会使得非零段数量+1
if(a[i-1]!=0&&a[i+1]!=0) cnt++;
//如果修改的位置是长度非1的非零段边缘的话,是不会改变非零段的数量的
//当修改这个位置,使得一个长度为”1“的非零段消失,就会使得非零短-1
if(a[i-1]==0 && a[i+1]==0) cnt--;
}
ans=max(ans,cnt);
}
} 注:最开始写的二分 然后得了20分
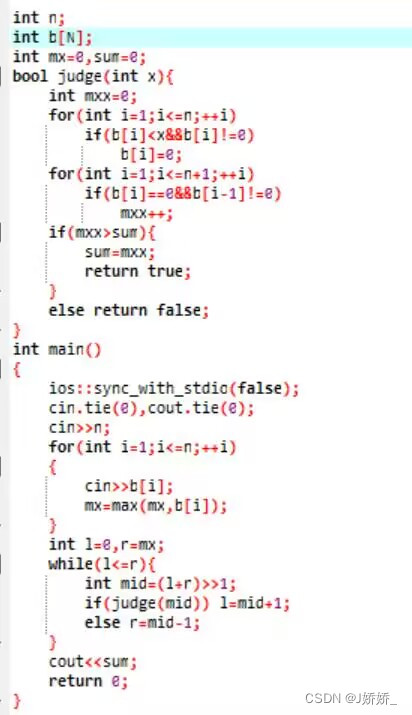
原因:不具有单调性
随着p增大,这个非零段的数量可能变大也可能变小,甚至比赛先变大再变小之类的,就是不确定的
计算机软件能力认证考试系统
202303-2 垦田计划
70分code:
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int n,m,k;
typedef pair<int,int>PII;//采用pair同时存储t和c
priority_queue<PII,vector<PII> > heap;//采用优先队列
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
int t,c;
cin>>t>>c;
heap.push({t,c});//压入队列
}
while(m>0)
{
PII t = heap.top();//取出当前基础耗时最大的
heap.pop();//记得删除最大点
//如果最大值不满足条件
if(t.first<=k)
{
heap.push(t);
break;
}
m -=t.second;//每次只缩减一天
t.first -= 1;
heap.push(t);
}
cout<<heap.top().first<<endl;//输出基础耗时最大的值
return 0;
}
100分code:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+9;
typedef long long ll;
ll n,m,k;
ll c[N],t[N];
bool check(ll mid){
//检查天数mid是否可行
ll sum=0;
for(int i=1;i<=n;++i)
{
sum+=c[i]*max(0ll,t[i]-mid);
}
return sum<=m;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>k;
for(int i=1;i<=n;++i) cin>>t[i]>>c[i];
//二分最小天数,答案可选范围是[k,inf]
ll l=k-1,r=2e18;
while(l+1!=r)//l<r
{
ll mid=(l+r)>>1;
//如果mid可行,说明这个限制天数mid偏大,可以再变小,所以r=mid
if(check(mid))r=mid;
else l=mid;
}
cout<<r<<'\n';
return 0;
} 特征:确定了最大天数的情况下可以O(n)计算代价
并且代价越大,天数不会变大,所以具有单调性
202212-2 训练计划
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+9;
typedef long long ll;
//st[i]表示i项目的最早开始时间,ed[i]表示i项目的最晚开始时间
int p[N],t[N],st[N],ed[N];
//nex[i]存放i的所有后继
vector<int> nex[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n,m;cin>>n>>m;
for(int i=1;i<=m;++i)
{
cin>>p[i];
//记录所有后继点
nex[p[i]].push_back(i);
}
for(int i=1;i<=m;++i) cin>>t[i];
bool ans=true;
for(int i=1;i<=m;++i)
{
//如果有前驱,就是前驱的结束时间,否则就是从1开始
st[i]=p[i]?st[p[i]]+t[p[i]]:1;
//这里判断是否存在某个项目超出时间限制n
if(st[i]+t[i]-1>n) ans=false;
}
for(int i=1;i<=m;++i) cout<<st[i]<<" \n"[ i==m ];
//如果不能在n天内完成,就直接结束
if(!ans) return 0;
//注意这里一定要倒这遍历,
//这样才能保证nex[i]中的所有ed已经算出
for(int i=m;i>=1;--i){
ed[i]=n-t[i]+1;//初始化为最大(即没有后继的情况)
//为了使得所有后继点的结束时间都在n以内,ed[i]应该取小
}
for(int i=1;i<=m;++i) cout<<ed[i]<<" \n"[i==m];
return 0;
} csp-
| 试题编号: | 202012-2 |
| 试题名称: | 期末预测之最佳阈值 |
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
vector<int> a, b, c;
int main()
{
int n;cin >> n;
for(int i = 1;i <= n; ++ i)
{
int y, res;cin >> y >> res;
//分组存储
if(res)a.push_back(y);
else b.push_back(y);
c.push_back(y);
}
sort(a.begin(), a.end());
sort(b.begin(), b.end());
sort(c.begin(), c.end());
int ans = c[0], mx = 0;
//c数组升序
for(const auto &thr : c)
{
int sum = 0;
//找出a中 >= thr 的数字的个数
sum += a.size() - (lower_bound(a.begin(), a.end(), thr) - a.begin());
//找出b中 < thr 的数字的个数
sum += lower_bound(b.begin(), b.end(), thr) - b.begin();
//当sum超过mx时,此时的thr肯定比之前的ans更好
if(sum >= mx)ans = thr, mx = sum;
}
cout << ans << '\n';
return 0;
}