快速排序 详解
- 快速排序
- 1. 挖坑法
- 2. 左右指针法 (Hoare 法)
- 3. 前后指针法
- 4. 快排非递归
- 代码优化
排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
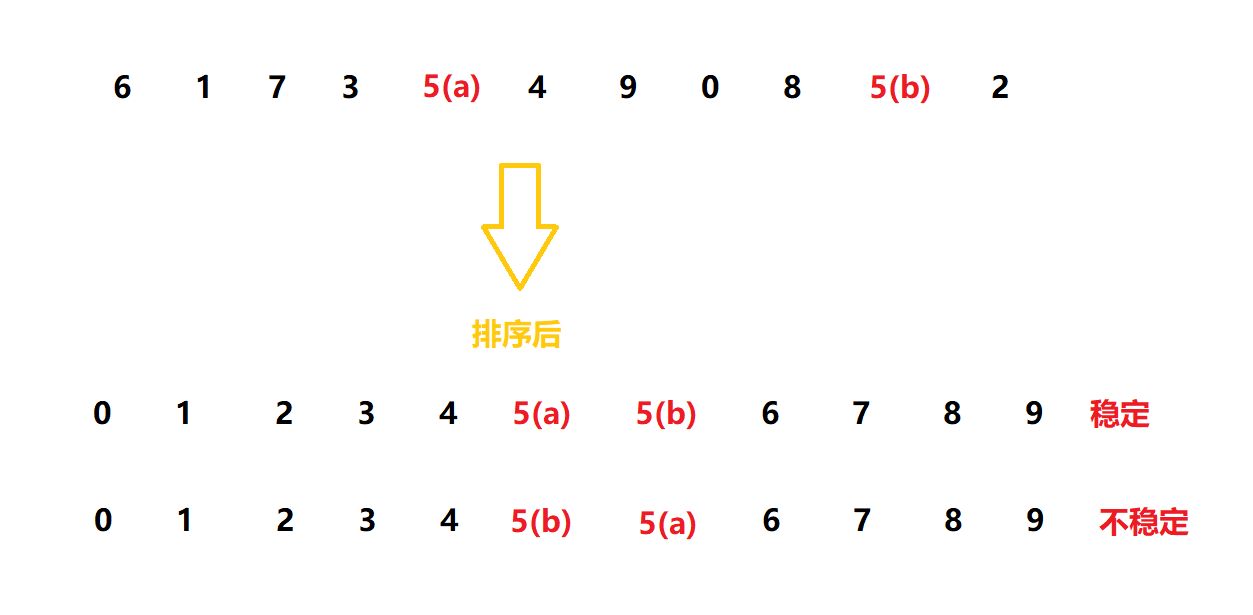
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i] = r[j], 且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
(注意稳定排序可以实现为不稳定的形式, 而不稳定的排序实现不了稳定的形式)
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
快速排序
快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1. 挖坑法
-
选择基准元素:从待排序的数组中选择一个元素作为基准(pivot)。通常情况下,可以选择第一个元素、最后一个元素、中间元素或者随机选择一个元素作为基准。
-
分割数组:从数组的两端开始,分别设置两个指针,一个从左边(low指针)开始,一个从右边(high指针)开始,分别向中间移动,直到它们相遇。在移动过程中,通过比较元素与基准的大小关系,找到一个大于基准的元素和一个小于基准的元素,并将它们互换位置。
-
继续分割:重复步骤2,直到low指针和high指针相遇。在此过程中,将小于基准的元素移到基准的左侧,将大于基准的元素移到基准的右侧,形成三个区域。
-
递归排序:对左侧小于基准的区域和右侧大于基准的区域,分别递归地应用快速排序算法。
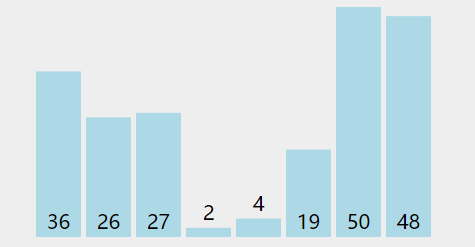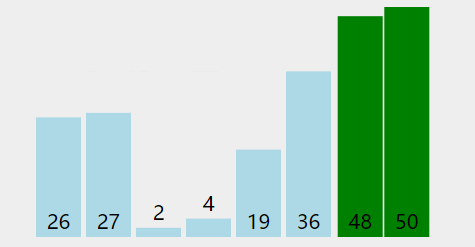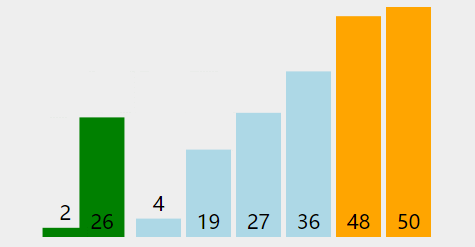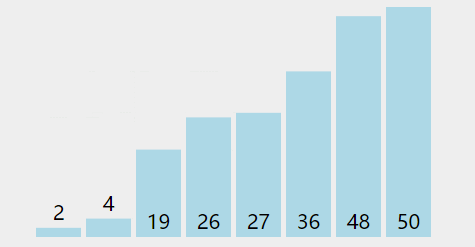
public static void quickSort(int[] arr) {
int len = arr.length;
partition(arr, 0, len-1);
}
public static void partition(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int pivot = left;
int value = arr[left];
// 从两边开始遍历
int begin = left;
int end = right;
while (begin < end) {
// 注意一定要带上 ==, 不然死循环
while (begin < end && arr[end] >= value) {
end--;
}
// 右边找到小于 value 的值
arr[pivot] = arr[end];
// end 变为 坑
pivot = end;
while (begin < end && arr[begin] <= value) {
begin++;
}
// 左边找到大于 value 的值
arr[pivot] = arr[begin];
// begin 变为坑
pivot = begin;
}
// value 找到自己的正确位置
arr[pivot] = value;
// 递归左边和右边
partition(arr, left, pivot-1);
partition(arr, pivot+1, right);
}
2. 左右指针法 (Hoare 法)
从两边开始, 左边找到比基准值大的, 右边找比基准值小的, 找到后, 两边交换, 一直到左右两个指针相遇, 相遇位置即为基准值的正确位置, 然后递归确定左右两边的区间元素的位置。
public static void quickSort(int[] arr) {
int len = arr.length;
partition(arr, 0, len-1);
}
public static void partition(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int value = arr[left];
int begin = left;
int end = right;
while (begin < end) {
// 注意一定要带上 ==, 不然死循环
while (begin < end && arr[end] >= value) {
end--;
}
while (begin < end && arr[begin] <= value) {
begin++;
}
swap(arr, begin, end);
}
swap(arr, left, begin);
partition(arr, left, begin-1);
partition(arr, begin+1, right);
}
public static void swap (int[] arr, int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
}
3. 前后指针法
后面的指针指向小于基准值的最后一个, 前面的指针一直往后找, 找到小于基准值的就与后面指针的下一个位置交换, 后面的指针 ++, 直到前面的指针遍历完, 最后后面的指针的位置, 就是基准值的正确位置。然后再递归确定左右区间的元素的位置。
public static void quickSort(int[] arr) {
int len = arr.length;
partition(arr, 0, len-1);
}
public static void partition(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int value = arr[left];
// 前后指针
int end = left;
int front = left + 1;
while (front <= right) {
if (arr[front] < value) {
swap(arr, end+1, front);
end++;
}
front++;
}
swap(arr, left, end);
// 递归左边和右边
partition(arr, left, end-1);
partition(arr, end+1, right);
}
public static void swap (int[] arr, int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
}
4. 快排非递归
使用栈记录要排序的区间
public static void quickSortNonR(int[] arr) {
int len = arr.length;
Stack<Integer> stack = new Stack<>();
stack.push(arr.length-1);
stack.push(0);
while (!stack.isEmpty()) {
int left = stack.pop();
int right = stack.pop();
if (left >= right) {
continue;
}
int pivot = left;
int value = arr[left];
// 从两边开始遍历
int begin = left;
int end = right;
while (begin < end) {
// 注意一定要带上 ==, 不然死循环
while (begin < end && arr[end] >= value) {
end--;
}
// 右边找到小于 value 的值
arr[pivot] = arr[end];
// end 变为 坑
pivot = end;
while (begin < end && arr[begin] <= value) {
begin++;
}
// 左边找到大于 value 的值
arr[pivot] = arr[begin];
// begin 变为坑
pivot = begin;
}
// value 找到自己的正确位置
arr[pivot] = value;
// 右区间
stack.push(right);
stack.push(pivot+1);
// 左区间
stack.push(pivot-1);
stack.push(left);
}
}
代码优化
优化一:
三数取中:
当我们找基准值时, 基准值越靠近是中位数,每次都近似于将一个大的区间分成两个相等的区间, 那么时间复杂度越低, 越靠近是 O(N*logN), 最坏的情况下, 每次确定一个元素, 即分成的两个区间其中一个只有一个元素, 那么如果每次都是这样的话, 最终的时间复杂度为 O(N*N), 所以选择基准值时, 越靠近中位数越好。
这里面以前后指针为例使用了 三数取中
public static void quickSort(int[] arr) {
int len = arr.length;
partition(arr, 0, len-1);
}
/**
* 前后指针
*/
public static void partition(int[] arr, int left, int right) {
if (left >= right) {
return;
}
// 三数取中
int midIndex = getMidIndex(arr, left, right);
swap(arr, left, midIndex);
int value = arr[left];
// 前后指针
int end = left;
int front = left + 1;
while (front <= right) {
if (arr[front] < value) {
swap(arr, end+1, front);
end++;
}
front++;
}
swap(arr, left, end);
// 递归左边和右边
partition(arr, left, end-1);
partition(arr, end+1, right);
}
public static int getMidIndex(int[] arr, int left, int right) {
int midIndex = ((right - left) >> 1) + left;
if (arr[left] <= arr[midIndex]) {
if (arr[midIndex] <= arr[right]) {
return midIndex;
} else {
if (arr[left] >= arr[right]) {
return left;
} else {
return right;
}
}
} else {
if (arr[midIndex] >= arr[right]) {
return midIndex;
} else {
if (arr[left] >= arr[right]) {
return right;
} else {
return left;
}
}
}
}
public static void swap (int[] arr, int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
}
优化二:
小区间优化, 当区间中元素数量比较少时,区间中元素本身就接近有序, 使用直接插入排序能提高效率 (直接插入排序)
假如说有 100W 个数据, 就会调用 100W 次 partition 函数, 但是光最后两层就会调用近 80W 次, 所以使用小区间优化提高效率。
直接插入排序
public static void insertSort(int[] arr) {
int len = arr.length;
for (int i = 1; i < len; i++) {
// 从已经有序的位置从后往前开始比较
int key = arr[i];
int end = i-1;
while (end >= 0 && arr[end] > key) {
// 数据往后挪
arr[end+1] = arr[end];
end--;
}
// 找到了合适位置, 就插入进去
arr[end+1] = key;
}
}
在快排中使用小区间优化
/**
* 直接插入排序
*/
public static void insertSort(int[] arr, int left, int right) {
for (int i = left+1; i <= right; i++) {
// 从已经有序的位置从后往前开始比较
int key = arr[i];
int end = i-1;
while (end >= 0 && arr[end] > key) {
// 数据往后挪
arr[end+1] = arr[end];
end--;
}
// 找到了合适位置, 就插入进去
arr[end+1] = key;
}
}
public static void quickSort(int[] arr) {
int len = arr.length;
partition(arr, 0, len-1);
}
public static void partition(int[] arr, int left, int right) {
if (left >= right) {
return;
}
// 小区间优化, 当数组中元素个数 <= 100 个时使用直接插入排序
// 主要是减少了递归的次数
if (right - left + 1 <= 100) {
insertSort(arr, left, right);
return;
}
// 三数取中
int midIndex = getMidIndex(arr, left, right);
swap(arr, left, midIndex);
int value = arr[left];
// 前后指针
int end = left;
int front = left + 1;
while (front <= right) {
if (arr[front] < value) {
swap(arr, end+1, front);
end++;
}
front++;
}
swap(arr, left, end);
// 递归左边和右边
partition(arr, left, end-1);
partition(arr, end+1, right);
}
总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
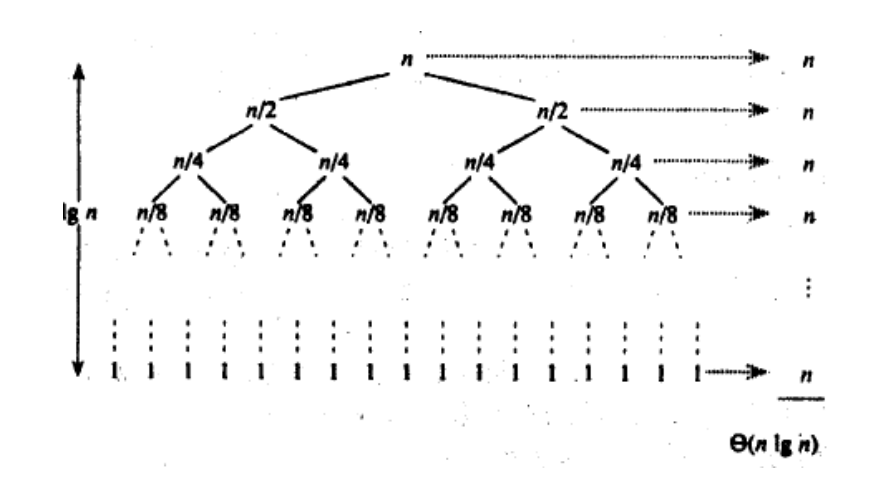
- 时间复杂度: O (N*logN)
- 空间复杂度: O(logN)
- 是不稳定排序
- 对数据比较敏感: 当数据本身就是有序时, 情况最坏, 因为每次只能确定一个数据, 时间复杂度为 O(N*N)
好啦, 以上就是对快速排序的讲解, 希望能帮到你 !
评论区欢迎指正 !


![[当人工智能遇上安全] 8.基于API序列和机器学习的恶意家族分类实例详解](https://img-blog.csdnimg.cn/fc259b57eb4b4df297903a76b1772ffc.jpeg#pic_center)


![【洛谷 P1328】[NOIP2014 提高组] 生活大爆炸版石头剪刀布 题解(模拟+向量)](https://img-blog.csdnimg.cn/img_convert/02b1ed72aacb231ea81d399df7574439.png)