最长递增子序列

news2024/11/25 10:23:56

题目链接

最长递增子序列

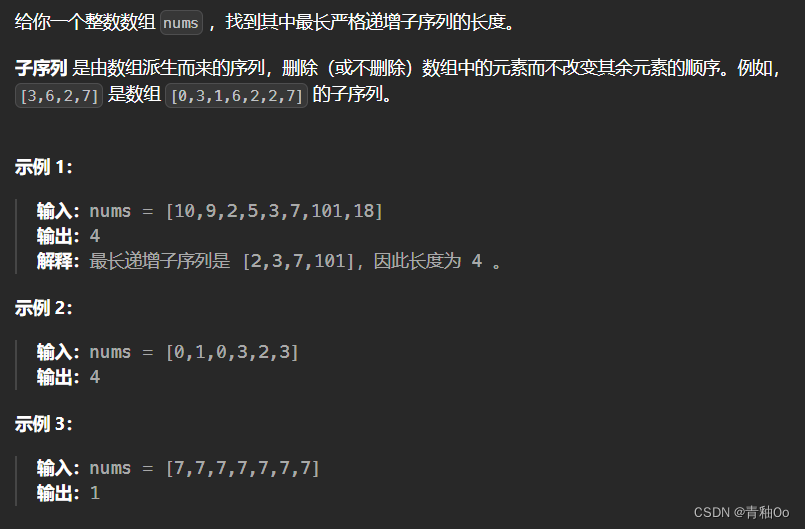
题目描述

注意点

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序

解答思路

初始想到使用动态规划解决本题，对于任意位置元素，找到前面比其值更小的元素，并根据前面元素的最长递增子序列计算出该元素的最长递增子序列，遍历完整个数组后就能得到结果，但是时间复杂度为O(n²)，比较耗时
参考题解使用贪心算法+二分查找解决本题，从头开始遍历数组，想要找到最长递增子序列，则相同长度的子序列的尾节点应该尽可能小，所以在遍历到某个元素x时，应该用x覆盖掉比x大的元素中最小的那个尾节点，而找到比x大的元素中最小的那个尾节点则应该用二分查找，时间复杂度为O(nlogn)

代码

方法一：

// 动态规划
class Solution {
    public int lengthOfLIS(int[] nums) {
        int res = 0;
        int n = nums.length;
        int[] dp = new int[n];
        dp[0] = 1;
        for (int i = 0; i < n; i++) {
            dp[i] = 1;
            for (int j = i - 1; j >= 0; j--) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

方法二：

// 贪心+二分查找
class Solution {
    public int lengthOfLIS(int[] nums) {
        int res = 0;
        // 存储不同长度中末尾元素的最小值
        int[] tails = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            int left = 0, right = res;
            // 当前元素覆盖掉比它大的元素中最小的那个
            while (left < right) {
                int mid = (left + right) / 2;
                if (nums[i] > tails[mid]) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            tails[left] = nums[i];
            if (right == res) {
                res++;
            }
        }
        return res;
    }
}