一、递推
95.费解的开关
#include<iostream>
#include<cstring>
using namespace std;
const int N = 8;
char a[N][N],s[N][N];
int T;
int ans=20,cnt;
int dir[5][2]={1,0,-1,0,0,1,0,-1,0,0};
void turn(int x,int y)
{
for(int i=0;i<5;i++)
{
int xx = x+dir[i][0];
int yy = y+dir[i][1];
if(xx<0 || yy<0 || xx>=5 || yy>=5) continue;
if(a[xx][yy]=='0') a[xx][yy]='1';
else a[xx][yy]='0';
}
cnt++;
}
void solve()
{
ans = 10;
for(int i=0;i<5;i++) cin>>s[i];
for(int i=0;i< 1<<5 ;i++)
{
cnt=0;
memcpy(a,s,sizeof a);
for(int j=0;j<5;j++)
{
if((i>>j)&1) turn(0,j);
}
for(int j=1;j<5;j++)
{
for(int k=0;k<5;k++)
{
if(a[j-1][k]=='0') turn(j,k);
}
}
for(int j=0;j<5;j++)
{
if(a[4][j]!='1') break;
else if(j==4) ans=min(ans,cnt);
}
}
if(ans<=6) cout<<ans<<endl;
else cout<<"-1"<<endl;
}
int main()
{
cin>>T;
while(T--)
solve();
return 0;
}
二、递归
1.数的遍历
一个二叉树,树中每个节点的权值互不相同。
现在给出它的后序遍历和中序遍历,请你输出它的层序遍历。
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 100;
int n;
int a[N],b[N],p[N];
int l[N],r[N],tr[N];
int build(int al,int ar,int bl,int br)
{
if(al>ar) return -1;
int val = a[ar];
int pos = p[val];
l[val] = build(al,al+pos-bl-1,bl,pos-1);
r[val] = build(al+pos-bl,ar-1,pos+1,br);
return val;
}
void bfs()
{
queue<int>q;
q.push(a[n]);
while(!q.empty())
{
int x = q.front();
q.pop();
cout<<x<<" ";
if(l[x]!=-1) q.push(l[x]);
if(r[x]!=-1) q.push(r[x]);
}
}
int main()
{
memset(l,-1,sizeof l);
memset(r,-1,sizeof r);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i],p[b[i]]=i;
build(1,n,1,n);
bfs();
return 0;
}
2.约数之和
假设现在有两个自然数 A和 B,S 是
A
B
A^B
AB的所有约数之和。
请你求出 S mod 9901的值是多少。
解:
- 先将 A A A做质因数分解, A = p 1 t 1 ⋅ p 2 t 2 ⋅ . . . ⋅ p k t k A = p_1^{t_1} \cdot p_2^{t_2} \cdot ... \cdot p_k^{t_k} A=p1t1⋅p2t2⋅...⋅pktk。
A 的所有约数之和为:
(
p
1
0
+
p
1
1
+
.
.
.
+
p
1
t
1
)
×
(
p
2
0
+
p
2
1
+
.
.
.
+
p
2
t
2
)
×
.
.
.
×
(
p
k
0
+
p
k
1
+
.
.
.
+
p
k
t
k
)
(p_1^0 + p_1^1+...+p_1^{t_1}) \times (p_2^0 + p_2^1+...+p_2^{t_2}) \times ... \times (p_k^0 + p_k^1+...+p_k^{t_k})
(p10+p11+...+p1t1)×(p20+p21+...+p2t2)×...×(pk0+pk1+...+pktk)
- 那么, A B = p 1 t 1 B ⋅ p 2 t 2 B ⋅ . . . ⋅ p k t k B A^B = p_1^{t_1B} \cdot p_2^{t_2B} \cdot ... \cdot p_k^{t_kB} AB=p1t1B⋅p2t2B⋅...⋅pktkB。
A^B 的所有约数之和为:
(
p
1
0
+
p
1
1
+
.
.
.
+
p
1
t
1
B
)
×
(
p
2
0
+
p
2
1
+
.
.
.
+
p
2
t
2
B
)
×
.
.
.
×
(
p
k
0
+
p
k
1
+
.
.
.
+
p
k
t
k
B
)
(p_1^0 + p_1^1+...+p_1^{t_1B}) \times (p_2^0 + p_2^1+...+p_2^{t_2B}) \times ... \times (p_k^0 + p_k^1+...+p_k^{t_kB})
(p10+p11+...+p1t1B)×(p20+p21+...+p2t2B)×...×(pk0+pk1+...+pktkB)
- 设 s u m ( p , k ) = p 0 + p 1 + . . . + p k sum(p,k) = p^0 + p^1 + ... + p^k sum(p,k)=p0+p1+...+pk
k为奇数:
s
u
m
(
p
,
k
)
=
(
p
k
2
+
1
+
1
)
⋅
s
u
m
(
p
,
k
2
)
sum(p,k) = (p^{\frac{k}{2}+1}+1) \cdot sum(p,\frac{k}{2})
sum(p,k)=(p2k+1+1)⋅sum(p,2k)
k为偶数:
s
u
m
(
p
,
k
)
=
s
u
m
(
p
,
k
−
1
)
+
p
k
sum(p,k)=sum(p,k-1) + p^k
sum(p,k)=sum(p,k−1)+pk
代码:
#include<iostream>
using namespace std;
const int MOD = 9901;
int a,b;
int ans=1;
int qmi(int a,int b)
{
int res = 1;
a %= MOD;
while(b)
{
if(b&1) res = res*a % MOD;
a = a*a % MOD;
b >>= 1;
}
return res;
}
int sum(int p,int k)
{
if(k==0) return 1;
if(k&1) return (qmi(p,k/2+1)+1)*sum(p,k/2) % MOD;
else return qmi(p,k)+sum(p,k-1) % MOD;
}
int main()
{
cin>>a>>b;
for(int i=2;i<=a;i++)
{
int s = 0;
while(a%i==0)
{
a /= i;
s++;
}
if(s) ans = ans*sum(i,b*s) % MOD;
}
if(!a) puts("0");
else cout<<ans<<endl;
return 0;
}
3.分形之城
市的规划在城市建设中是个大问题。
不幸的是,很多城市在开始建设的时候并没有很好的规划,城市规模扩大之后规划不合理的问题就开始显现。
而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
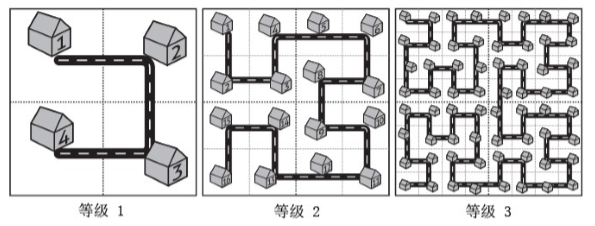
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。
对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。
虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 N,编号为 A 和 B 的两个街区的直线距离是多少。
街区的距离指的是街区的中心点之间的距离,每个街区都是边长为 10 米的正方形。
思路:先计算数字A,B在n级城市的哪一块,再计算在n-1级城市的x,y坐标,递归综合得到A、B的坐标。
难点:坐标变换。
第一块:xy坐标互换;
第二块、第三块:无变化;
第四块:先逆时针旋转90°,再y坐标对称变换。
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
typedef pair<ll,ll>PLL;
ll T;
ll n,a,b;
PLL get(ll n,ll s)
{
if(n==0) return {0,0};
ll len = 1 << (n-1);
ll sum = len*len;
PLL p = get(n-1,s%sum);
ll x = p.first , y = p.second;
ll block = s / sum;
if(block==0) return {y,x};
else if(block==1) return {x,y+len};
else if(block==2) return {x+len,y+len};
else if(block==3) return {len*2 - 1 - y , len - 1 - x};
}
void solve()
{
cin>>n>>a>>b;
PLL pa = get(n,a-1);
PLL pb = get(n,b-1);
double dx = pa.first - pb.first;
double dy = pa.second - pb.second;
printf("%.0lf\n",sqrt(dx*dx+dy*dy)*10);
}
int main()
{
cin>>T;
while(T--)
solve();
return 0;
}
3.并查集
1.T333099 连通块中点的数量
给定一个包含 n 个点( 编号为 1~n )的无向图,初始时图中没有边。
现在要进行 m
个操作,操作共有三种:
1.C a b,在点a和点b之间连一条边,a和b可能相等;
2.Q1 a b,询问点a和点b是否在同一个连通块中,a
和 b 可能相等;
3.Q2 a,询问点 a 所在连通块中点的数量;
#include<iostream>
using namespace std;
const int N = 1000005;
int n,m;
string op;
int u,v;
int f[N],w[N];
int Find(int x)
{
if(f[x]!=x) f[x]=Find(f[x]);
return f[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) f[i]=i,w[i]=1;
for(int i=1;i<=m;i++)
{
cin>>op;
if(op=="C")
{
cin>>u>>v;
u = Find(u);
v = Find(v);
// 一定要先判断两个点是否在一个集合,否则数量会出错误(翻倍)
if(u!=v)
{
w[v]+=w[u];
f[u]=v;
}
}
else if(op=="Q1")
{
cin>>u>>v;
if(Find(u)==Find(v))
puts("Yes");
else
puts("No");
}
else
{
cin>>u;
u = Find(u);
cout<<w[u]<<endl;
}
}
return 0;
}
数量
2.自动程序分析
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设
x
1
,
x
2
,
x
3
,
⋯
x_1,x_2,x_3,\cdots
x1,x2,x3,⋯ 代表程序中出现的变量,给定
n
n
n 个形如
x
i
=
x
j
x_i=x_j
xi=xj 或
x
i
≠
x
j
x_i\neq x_j
xi=xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:
x
1
=
x
2
,
x
2
=
x
3
,
x
3
=
x
4
,
x
4
≠
x
1
x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1
x1=x2,x2=x3,x3=x4,x4=x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
思路:
先用并查集连通所有等式,再判断所有不等式,是否有不等式两边元素相等的,若有则不满足。
知识点:
离散化:
int s(int x)
{
if(!m.count(x)) m[x]=++idx;
return m[x];
}
#include<iostream>
#include<map>
#include<vector>
using namespace std;
const int N = 200005;
typedef pair<int,int>PII;
int T;
int n,u,v,e;
int f[N];
PII vec[N];
map<int,int>m;
int idx;
int s(int x)
{
if(!m.count(x)) m[x]=++idx;
return m[x];
}
int Find(int x)
{
if(x!=f[x]) f[x]=Find(f[x]);
return f[x];
}
void solve()
{
scanf("%d", &n);
for(int i=1;i<=2*n;i++) f[i]=i;
int cnt = 0;
idx=0;
m.clear();
for(int i=1;i<=n;i++)
{
scanf("%d%d%d", &u, &v, &e);
u = s(u) , v = s(v);
if(e==1)
{
u = Find(u);
v = Find(v);
f[u]=v;
}
else vec[++cnt] = {u,v};
}
for(int i=1;i<=cnt;i++)
{
u = vec[i].first;
v = vec[i].second;
if(Find(u)==Find(v))
{
puts("NO");
return;
}
}
puts("YES");
}
int main()
{
scanf("%d", &T);
while(T--)
solve();
return 0;
}
3.银河英雄传说
有一个划分为 N列的星际战场,各列依次编号为 1,2,…,N。
有 N 艘战舰,也依次编号为 1,2,…,N,其中第 i 号战舰处于第 i 列。
有 T条指令,每条指令格式为以下两种之一:
- M i j,表示让第 i 号战舰所在列的全部战舰保持原有顺序,接在第 j 号战舰所在列的尾部。
- C i j,表示询问第 i号战舰与第 j 号战舰当前是否处于同一列中,如果在同一列中,它们之间间隔了多少艘战舰。
现在需要你编写一个程序,处理一系列的指令。
解析:
用 f 数组记录战舰之间的连通性(是否在一列), sz 数组记录第 i 列有多少量战舰(即维护集合元素个数), d 数组维护结点 i 离其父节点的距离(初始所有结点都是根节点,d 均为0)
每次合并时(以将pa结点挂在pb上为例),只需将d[pa] = sz[pb] 即可完成操作。但还需更新 pa 所有子结点的 d 值,每个子结点 d 值需要增加的量为其父节点的 d 值(在Find函数中实现)
#include<iostream>
using namespace std;
const int N = 100005;
int n;
char op;
int a,b;
int f[N],d[N],sz[N];
int Find(int x)
{
if(f[x]!=x)
{
int root = Find(f[x]);
d[x] += d[f[x]];
f[x] = root;
}
return f[x];
}
int main()
{
for(int i=1;i<N;i++) f[i]=i,sz[i]=1;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>op>>a>>b;
int pa = Find(a) , pb = Find(b);
if(op=='M' && pa!=pb) //注意!必须在不同集合上才合并。
{
d[pa] = sz[pb];
f[pa] = pb;
sz[pb] += sz[pa];
}
else if(op=='C')
{
if(pa!=pb) puts("-1");
else cout<<max(0,abs(d[a]-d[b])-1)<<endl;
}
}
return 0;
}
4.食物链
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X 或 Y 比 N 大,就是假话;
- 当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
思路:用 f 数组记录动物间是否有联系,d 数组表示第 i 个结点到父节点的距离。
f[x] == f[y] : x 与 y 有联系。
d[y] = d[x] + 1 X可以吃Y
对于每句话,需要判断
1.X,Y之间之前是否有联系,如果有联系且与这句话相悖,ans++;
2.如果X,Y之间没有联系,那么
如果X与Y是同类,那么将X挂到Y上,并且更新PX离PY的距离为 d[y] - d[x] ,即表示X与Y为同类。
若果X可以吃Y,那么将X挂到Y上,并且更新PX离PY的距离为d[y] - d[x] + 1,表示X可以吃Y。
#include<iostream>
using namespace std;
const int N = 100005;
int n,m;
int op,x,y;
int f[N],d[N];
int ans;
int Find(int x)
{
if(f[x]!=x)
{
int root = Find(f[x]);
d[x] += d[f[x]];
f[x] = root;
}
return f[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=m;i++)
{
cin>>op>>x>>y;
if(x>n || y>n)
{
ans++;
continue;
}
int px = Find(x) , py = Find(y);
if(op==1)
{
if(px == py && (d[x]-d[y])%3) ans++;
else if(px != py)
{
d[px] = d[y] - d[x];
f[px] = py;
}
}
else
{
if(px == py && (d[x]-d[y]-1)%3) ans++;
else if(px != py)
{
d[px] = d[y] - d[x] + 1;
f[px] = f[py];
}
}
}
cout<<ans<<endl;
return 0;
}
5.奇偶游戏

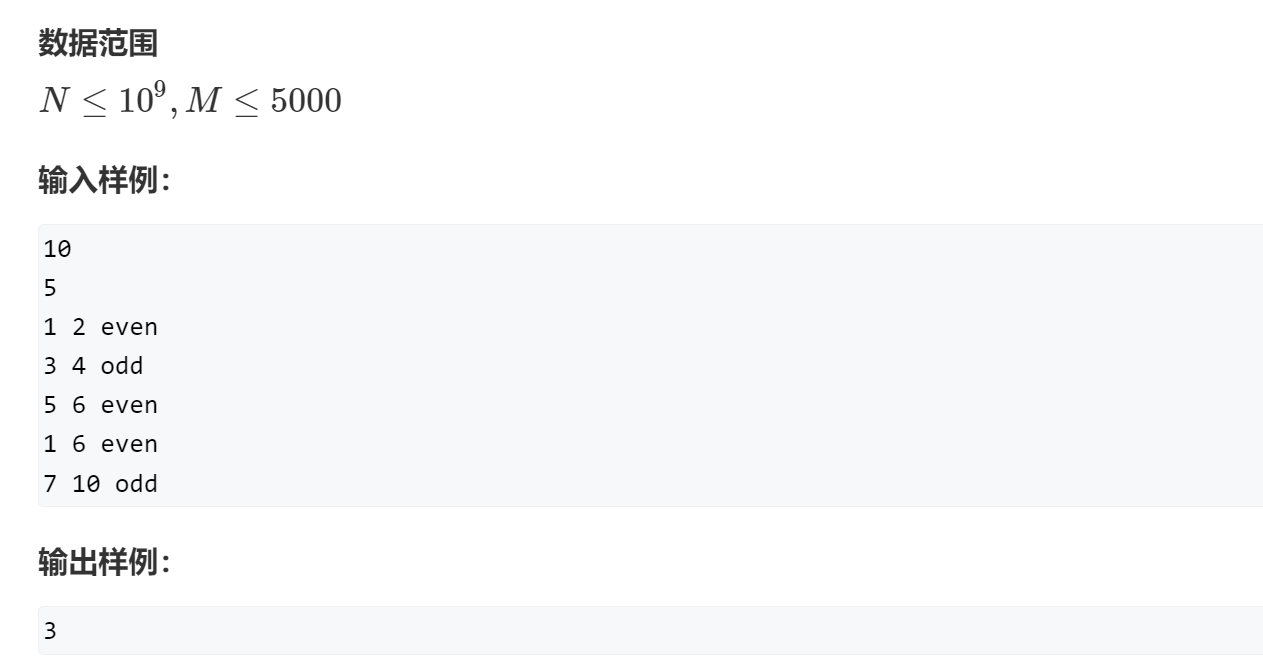
思路:
设 s 为初始数组的前缀和数组,若 l ~ r 和为奇数,则 s[l-1] 与 s[r] 的奇偶性不同,反之则相同。
利用数组 d 来确定每两个结点之间的关系,d[x]-d[y] mod 2 == 1 则代表奇偶性不同,反之相同。
#include<iostream>
#include<map>
using namespace std;
const int N = 100005;
int n,m;
map<int,int>ma;
int idx;
int l,r;
string op;
int f[N],d[N];
int ans;
int x,y,px,py;
int S(int x)
{
if(!ma.count(x)) ma[x]=++idx;
return ma[x];
}
int Find(int x)
{
if(x!=f[x])
{
int root = Find(f[x]);
d[x] += d[f[x]];
f[x] = root;
}
return f[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<N;i++) f[i]=i;
for(int i=1;i<=m;i++)
{
cin>>l>>r>>op;
if(ans>0) continue;
x = S(l-1) , y = S(r);
px = Find(x) , py = Find(y);
if(op == "even")
{
if(px == py && (d[x]-d[y])%2) ans = i;
else if(px != py)
{
d[px] = d[x]^d[y];
f[px] = py;
}
}
else
{
if(px == py && (d[x]-d[y])%2 == 0) ans = i;
else if(px != py)
{
d[px] = d[x]+d[y]+1;
f[px] = py;
}
}
}
if(!ans) cout<<m<<endl;
else cout<<ans-1<<endl;
return 0;
}
四、单调队列
1.滑动窗口

运用了双端队列
求最大值时,在每次插入新元素之前,先判断队头是否离开窗口,再将队尾所有小于当前值的元素pop出去。
#include<iostream>
#include <deque>
using namespace std;
const int N = 300005;
int n,m;
int a[N];
deque<int>q;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
if(!q.empty() && i-q.front()>=m) q.pop_front();
while(!q.empty() && a[i]<a[q.back()]) q.pop_back();
q.push_back(i);
if(i>=m) cout<<a[q.front()]<<" ";
}
cout<<endl;
while(!q.empty()) q.pop_back();
for(int i=1;i<=n;i++)
{
if(!q.empty() && i-q.front()>=m) q.pop_front();
while(!q.empty() && a[i]>a[q.back()]) q.pop_back();
q.push_back(i);
if(i>=m) cout<<a[q.front()]<<" ";
}
return 0;
}
2.最大自序和

#include<iostream>
#include<deque>
using namespace std;
const int N = 300005;
int n,m;
int a[N],s[N];
deque<int>q;
int ans=-3e9;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],s[i]=s[i-1]+a[i];
for(int i=1;i<=n;i++)
{
if(!q.empty() && i-q.front()>=m) q.pop_front();
while(!q.empty() && s[i-1]-s[q.back()-1]<=0) q.pop_back(); //错误 之前是s[i]-s[tail];
q.push_back(i);
ans = max(ans,s[i]-s[q.front()-1]);
}
cout<<ans<<endl;
return 0;
}
3.单调栈

#include<iostream>
#include<stack>
using namespace std;
const int N = 3000005;
int n;
int a[N],f[N];
stack<int>s;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=n;i>=1;i--)
{
while(!s.empty() && a[i]>=a[s.top()]) s.pop();
if(s.empty()) f[i]=0;
else f[i]=s.top();
s.push(i);
}
for(int i=1;i<=n;i++) printf("%d ",f[i]);
return 0;
}
4.烽火传递

#include<iostream>
#include<deque>
using namespace std;
const int N = 200005;
int n,m;
int a[N],f[N];
deque<int>q;
int ans = 1e9;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
q.push_back(0);
for(int i=1;i<=n;i++)
{
if(!q.empty() && i-q.front()>m) q.pop_front();
f[i] = f[q.front()] + a[i];
while(!q.empty() && f[i]<f[q.back()]) q.pop_back();
q.push_back(i);
}
for(int i=0;i<m;i++) ans=min(ans,f[n-i]);
cout<<ans<<endl;
return 0;
}
五、博弈论
1. Nim游戏
#include<iostream>
using namespace std;
int n;
int a;
int ans;
int main()
{
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>a;
ans^=a;
}
if(ans) puts("Yes");
else puts("No");
return 0;
}
2. 台阶-Nim游戏
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 100005;
ll a[N],res;
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>a[i];
for(int i=1;i<=n;++i)
{
if(i%2) res^=a[i];
}
if(res) puts("Yes");
else puts("No");
return 0;
}
3. 集合-Nim游戏
博弈论进阶之SG函数
#include<iostream>
#include<cstring>
#include<set>
#include<algorithm>
using namespace std;
int n,m,a;
int res;
int s[105],f[100005];
//当sg值为0时,为必败状态,因为他下一次无法转化为sg为0的状态,即无法转化成必败状态
//当sg值为非0时,为必胜状态,他的子集有sg为0的状态,因此可以转移为必败状态
int sg(int x)
{
if(f[x]!=-1) return f[x];
set<int>S;//装可以有x转移到的的状态的sg值
for(int i=0;i<m;++i)
{
if(x>=s[i]) S.insert(sg(x-s[i]));
}
//Mex函数,返回集合S中未出现的最小值
for(int i=0;;i++)
{
if(!S.count(i)) return f[x]=i;
}
}
int main()
{
memset(f,-1,sizeof f);
cin>>m;
for(int i=0;i<m;++i) cin>>s[i];
cin>>n;
for(int i=0;i<n;++i)
{
cin>>a;
res^=sg(a);
}
if(res) puts("Yes");
else puts("No");
return 0;
}
4. 拆分-Nim游戏
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_set>
using namespace std;
const int N = 105;
int n;
int f[N];
int res;
int sg(int x)
{
if(f[x]!=-1) return f[x];
unordered_set<int>S;
for(int i=0;i<x;i++)
{
for(int j=0;j<x;j++)
{
S.insert(sg(i)^sg(j));
}
}
for(int i=0;;i++)
{
if(!S.count(i)) return f[x]=i;
}
}
int main()
{
memset(f,-1,sizeof f);
cin>>n;
for(int i=1;i<=n;++i)
{
int x;
cin>>x;
res^=sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}
5.牛客
六、线性dp(进阶指南)
271. 杨老师的照相排列
用f[a][b][c][d][e]表示第1~5排人数为abcde的方案数。
第一排人数一定大于第二排人数,第二排人数一定大于第三排人数…
求f[a][b][c][d][e]时,可以假设将最后一个人放到第12345排,放到第一排时,需要保证a至少为1,且a-1>=b。意思为将最后一人放到第一排后,第一排至少有1个人,且放之前第一排人数大于第二排人数(为有效状态)。
#include<iostream>
#include<cstring>
using namespace std;
const int N = 32;
typedef long long LL;
int n;
int s[N];
LL f[N][N][N][N][N];
int main()
{
f[0][0][0][0][0]=1;
for(int a=0;a<N;a++)
for(int b=0;b<=a;b++)
for(int c=0;c<=b;c++)
for(int d=0;d<=c;d++)
for(int e=0;e<=d;e++)
{
if(a && a-1>=b) f[a][b][c][d][e]+=f[a-1][b][c][d][e];
if(b && b-1>=c) f[a][b][c][d][e]+=f[a][b-1][c][d][e];
if(c && c-1>=d) f[a][b][c][d][e]+=f[a][b][c-1][d][e];
if(d && d-1>=e) f[a][b][c][d][e]+=f[a][b][c][d-1][e];
if(e) f[a][b][c][d][e]+=f[a][b][c][d][e-1];
}
while(cin>>n && n)
{
memset(s,0,sizeof s); // 每次需要清空s,因为此次数据排数可能没以前多,会保留多于排的人数
for(int i=1;i<=n;i++) cin>>s[i];
cout<<f[s[1]][s[2]][s[3]][s[4]][s[5]]<<endl;
}
return 0;
}
272. 最长公共上升子序列
#include<iostream>
using namespace std;
const int N = 3005;
int n;
int a[N],b[N];
int f[N][N]; //以b[j]结尾的最大上升公共子序列长度
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<=n;i++)
{
int maxv = 0;
for(int j=1;j<=n;j++)
{
f[i][j]=f[i-1][j]; //不选a[i]的情况
//选a[i]的情况
// if(a[i]==b[j])
// {
// int maxv = 0; //找以b[1~j-1]结尾的最大值
// for(int k=1;k<j;k++)
// {
// //满足上升子序列才更新
// if(b[j]>b[k]) maxv = max(maxv,f[i-1][k]);
// }
// f[i][j]=max(f[i][j],maxv+1);
// }
if(a[i]>b[j-1]) maxv = max(maxv,f[i-1][j-1]); //因为该情况a[i]==b[j]
if(a[i]==b[j]) f[i][j]=max(f[i][j],maxv+1);
}
}
int ans =0;
for(int i=1;i<=n;i++) ans=max(ans,f[n][i]);
cout<<ans<<endl;
return 0;
}
277. 饼干
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 35, M = 5005;
int n,m;
int f[N][M]; //代表前i个小朋友分配j个糖果的最小怒气和
int ans[N],s[N];
struct Greedy
{
int id,x;
bool operator<(const Greedy a)const{
return x>a.x;
}
}g[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>g[i].x;
g[i].id = i;
}
sort(g+1,g+n+1);
for(int i=1;i<=n;i++) s[i]=s[i-1]+g[i].x;
memset(f,0X3f,sizeof f);
f[0][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=m;j++)
{
//假如最优分配方案中没有人有一个饼干,那么把他们每个人的饼干都减1,答案不变。
f[i][j]=f[i][j-i];
//假设有k个人分配得一个饼干
for(int k=1;k<=i && k<=j;k++)
{
f[i][j]=min(f[i][j],f[i-k][j-k]+(s[i]-s[i-k])*(i-k));
}
}
}
cout<<f[n][m]<<endl;
//回溯,h代表所有人饼干数减1的次数
int h = 0;
for(int i=n,j=m;i && j;)
{
if(j>=i && f[i][j]==f[i][j-i]) j-=i,h++;
else
{
for(int k=1;k<=i && k<=j;k++)
{
if(f[i][j]==f[i-k][j-k]+(s[i]-s[i-k])*(i-k))
{
for(int u=i-k+1;u<=i;u++)
ans[g[u].id]=1+h;
i-=k,j-=k;
break;
}
}
}
}
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
七、背包问题
278. 数字组合
把每个数字看成一个价值为i的物品,求总价值为m的方案数。(01背包)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100005;
int n,m;
int f[N],a[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
f[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=N-1;j>=a[i];j--)
{
f[j]+=f[j-a[i]];
}
}
cout<<f[m]<<endl;
return 0;
}
279. 自然数拆分
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
// 把每个数字看成一个价值为1,体积为1的物品
// 做完全背包问题求方案数
const int N = 100005, MOD = 2147483648;
typedef long long ll;
int n;
ll f[N];
int main()
{
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
f[j] = (f[j]+f[j-i])%MOD;
}
}
cout<<f[n]-1<<endl;
return 0;
}
280. 陪审团
三维dp+回溯
#include<iostream>
#include<cstring>
using namespace std;
const int N = 205, M = 25, base = 400;
int n,m;
int p[N],d[N];
int f[N][M][805]; //前i个人选j个且abs(d-p)=k的最大d+p值
bool st[N];
int T;
int main()
{
while(cin>>n>>m && (n||m))
{
T++;
memset(st, 0, sizeof st);
memset(f,-0X3f,sizeof f);
f[0][0][base]=0; //差值为0的f为0
for(int i=1;i<=n;i++) cin>>p[i]>>d[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<805;k++)
{
// 如果不选第i个人
f[i][j][k]=f[i-1][j][k];
int t = k-(p[i]-d[i]);
if(t<0 || t>805) continue;
if(j<1) continue;
f[i][j][k]=max(f[i][j][k],f[i-1][j-1][t]+d[i]+p[i]);
}
}
}
int i=n,j=m,k=0;
while(f[n][m][base-k]<0 && f[n][m][base+k]<0) k++;
if(f[n][m][base-k]>f[n][m][base+k]) k=base-k;
else k=base+k;
while(j)
{
if(f[i][j][k]==f[i-1][j][k]) i--; // 如果第i个人可以不选
else
{
st[i]=true;
k-=p[i]-d[i];
i--,j--;
}
}
int sp=0,sd=0;
for(int i=1;i<=n;i++)
{
if(st[i]) sp+=p[i],sd+=d[i];
}
printf("Jury #%d\n",T);
printf("Best jury has value %d for prosecution and value %d for defence:\n",sp,sd);
for(int i=1;i<=n;i++)
if(st[i]) printf("%d ",i);
puts("\n");
}
return 0;
}
281. 硬币
#include<iostream>
#include<cstring>
using namespace std;
const int N = 100005;
int n,m;
int a[N],c[N];
int f[N],g[N]; //f[i]代表i元是否可以被凑成
int main()
{
while(cin>>n>>m && n && m)
{
memset(f,0,sizeof f);
f[0]=1;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>c[i];
for(int i=1;i<=n;i++)
{
//g[j]表示在处理第i种硬币时,凑成面值j至少需要第i中硬币的个数
memset(g,0,sizeof g);
for(int j=a[i];j<=m;j++)
{
//如果j还没有被凑出,且j-a[i]已经被凑出,且凑出j-a[i]后还剩余第i中钱币。
if(!f[j] && f[j-a[i]] && g[j-a[i]]<c[i])
{
g[j] = g[j-a[i]]+1;
f[j] = 1;
}
}
}
int ans = 0;
for(int i=1;i<=m;i++)
if(f[i]) ans++;
cout<<ans<<endl;
}
return 0;
}
八、区间dp
282. 石子合并
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1005;
int n;
int a[N],s[N];
int f[N][N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
memset(f,0X3f,sizeof f);
for(int i=1;i<=n;i++) f[i][i]=0;
for(int len=2;len<=n;len++)
{
for(int l=1;l+len-1<=n;l++)
{
int r = l+len-1;
for(int k=l;k<r;k++)
{
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
}
}
}
cout<<f[1][n]<<endl;
return 0;
}
283. 多边形
#include<iostream>
#include<cstring>
using namespace std;
const int N = 105 , INF = 0X3f3f3f3f;
int n;
int num[N];
char op[N];
int f[N][N],g[N][N];
int ans;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>op[i]>>num[i];
op[i+n]=op[i];
num[i+n]=num[i];
}
for(int len=1;len<=n;len++)
{
//for(int l=1;l<=n;l++)
for(int l=1;l+len-1<=2*n;l++)
{
int r = l+len-1;
if(len==1)
{
f[l][r]=g[l][r]=num[l];
continue;
}
f[l][r]=-INF,g[l][r]=INF;
for(int k=l;k<r;k++)
{
char ch = op[k+1];
int minl = g[l][k],minr = g[k+1][r];
int maxl = f[l][k],maxr = f[k+1][r];
if(ch=='t')
{
f[l][r]=max(f[l][r],maxl+maxr);
g[l][r]=min(g[l][r],minl+minr);
}
else
{
int x1 = minl * minr; // 负数乘负数
int x2 = maxl * maxr; // 正数乘正数
int x3 = maxl * minr; //
int x4 = minl * maxr;
f[l][r] = max(f[l][r],max(max(x1,x2),max(x3,x4)));
g[l][r] = min(g[l][r],min(min(x1,x2),min(x3,x4)));
}
}
}
}
for(int i=1;i<=n;i++) ans = max(ans,f[i][i+n-1]);
cout<<ans<<endl;
for(int i=1;i<=n;i++)
if(ans==f[i][i+n-1]) cout<<i<<" ";
return 0;
}
284. 金字塔
#include<iostream>
#include<cstring>
using namespace std;
const int N = 305 , MOD = 1e9;
typedef long long ll;
int n;
char s[N];
ll f[N][N];
int main()
{
cin>>(s+1);
n = strlen(s+1);
for(int len=1;len<=n;len++)
{
for(int l=1;l+len-1<=n;l++)
{
int r = l+len-1;
if(len==1) f[l][r]=1;
else if(s[l]==s[r])
{
for(int k=l;k<r;k+=2)
{
//找最后一个子树
if(s[k]==s[r])
f[l][r] = (f[l][r]+f[l][k]*f[k+1][r-1])%MOD;
}
}
}
}
cout<<f[1][n]<<endl;
return 0;
}
九、树形dp
285. 没有上司的舞会
#include<iostream>
#include<cstring>
using namespace std;
const int N = 200005;
int n;
int w[N];
int f[N],g[N]; //f[x]代表x去宴会,及其下属的总快乐指数;g[x]为x不去宴会
int l,k,root;
int ne[N],to[N],head[N],idx;
bool st[N];
void add(int u,int v)
{
idx++;
ne[idx]=head[u];
to[idx]=v;
head[u]=idx;
}
void dfs(int x)
{
f[x] = w[x];
for(int i=head[x];~i;i=ne[i])
{
int y = to[i];
dfs(y);
f[x] += g[y];
g[x] += max(f[y],g[y]);
}
}
int main()
{
memset(head,-1,sizeof head);
cin>>n;
for(int i=1;i<=n;i++) cin>>w[i];
for(int i=1;i<n;i++)
{
cin>>l>>k;
st[l]=true;
add(k,l);
}
for(int i=1;i<=n;i++)
if(!st[i]) root = i;
dfs(root);
cout<<max(f[root],g[root]);
return 0;
}
286. 选课
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1005;
int n,m;
int w[N];
int x;
int f[N][N]; //以i为根节点,选j门课的最大学分数
int ne[N],head[N],to[N],idx;
bool st[N];
int ans;
void add(int u,int v)
{
idx++;
ne[idx]=head[u];
to[idx]=v;
head[u]=idx;
}
void dfs(int x)
{
for(int i=head[x];~i;i=ne[i])
{
int y = to[i];
dfs(y);
for(int j=m-1;j>=0;j--)
{
for(int k=0;k<=j;k++)
{
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
}
}
}
for(int i=m;i>=1;i--) f[x][i]=f[x][i-1]+w[x];
f[x][0]=0;
}
int main()
{
memset(head,-1,sizeof head);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>x>>w[i];
add(x,i);
}
m++; //默认要选0号课程(虚拟根节点)
dfs(0);
cout<<f[0][m]<<endl;
return 0;
}
287. 积蓄程度
#include<iostream>
#include<cstring>
using namespace std;
const int N = 400005 , INF = 0X3f3f3f3f;
int T,n;
int ne[N],head[N],to[N],w[N],idx;
int f[N],d[N],deg[N];
int x,y,z;
void add(int u,int v,int dis)
{
idx++;
ne[idx] = head[u];
to[idx] = v;
w[idx] = dis;
head[u] = idx;
}
//d[i]代表以root为根,从结点i向下流的最大流量
int dfs_d(int x,int fa)
{
if(deg[x]==1) return f[x]=INF;
for(int i=head[x];~i;i=ne[i])
{
int y = to[i];
if(y==fa) continue;
d[x] += min(w[i],dfs_d(y,x));
}
return d[x];
}
//f[i]代表第i个结点的最大流量
int dfs_f(int x,int fa)
{
for(int i=head[x];~i;i=ne[i])
{
int y = to[i];
if(y==fa) continue;
if(deg[y]==1) f[y] = min(w[i],f[x]-w[i]);
else
{
f[y] = d[y] + min(f[x]-min(d[y],w[i]),w[i]);
dfs_f(y,x);
}
}
return f[x];
}
void solve()
{
memset(head,-1,sizeof head);
memset(deg,0,sizeof deg);
memset(f,0,sizeof f);
memset(d,0,sizeof d);
idx = 0;
cin>>n;
for(int i=1;i<n;i++)
{
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
deg[x]++,deg[y]++;
}
int root = 1;
while(root<=n && deg[root]==1) root++;
if(root>n)
{
cout<<w[1]<<endl;
return;
}
dfs_d(root,-1);
f[root] = d[root];
dfs_f(root,-1);
int ans = 0;
for(int i=1;i<=n;i++)
ans = max(ans,f[i]);
cout<<ans<<endl;
}
int main()
{
cin>>T;
while(T--)
solve();
return 0;
}