本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

谷歌 Google 1、亚马逊 1
苹果 Apple、Facebook、高盛集团 Goldman Sachs、微软 Microsoft、优步 Uber

在一个二维平面空间中，给你 n 个点的坐标。问，是否能找出一条平行于 y 轴的直线，让这些点关于这条直线成镜像排布？

注意：题目数据中可能有重复的点。

示例 1：

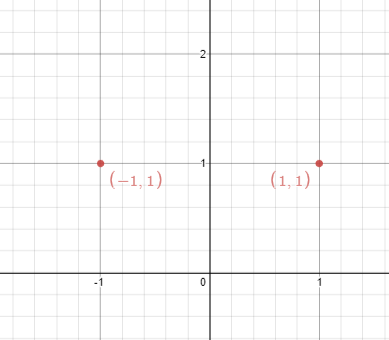
输入：points = [[1,1],[-1,1]]
输出：true
解释：可以找出 x = 0 这条线。

示例 2：

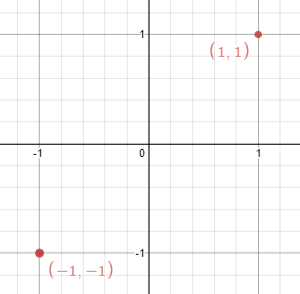
输入：points = [[1,1],[-1,-1]]
输出：false
解释：无法找出这样一条线。

提示：

• n == points.length
• 1 <= n <= 10^4
• -10^8 <= points[i][j] <= 10^8

进阶： 你能找到比 $O(n^2)$ 更优的解法吗？

---

解法 数学+哈希表

先求集合左右边界，找到可能的中线——如果可行，那么该直线必然是 x = ( min ⁡ { p o i n t s [ 0 ] } + max ⁡ { p o i n t s [ 0 ] } ) 2 x = \dfrac {(\min \{ points[0] \} + \max \{ points[0] \} ) }{2} x=2(min{points[0]}+max{points[0]})​
然后对集合内所有点，按所在行验证是否有「关于中线的镜像点」。

一个坑：只要看起来是镜像对称即可，不一定要两两配对。因此可以直接去重。

class Solution:
    def isReflected(self, points: List[List[int]]) -> bool:
        s = min(points)[0] + max(points)[0]
        vis = { (x, y) for x, y in points}
        return all( (s - x, y) in vis for x, y in vis)