题目

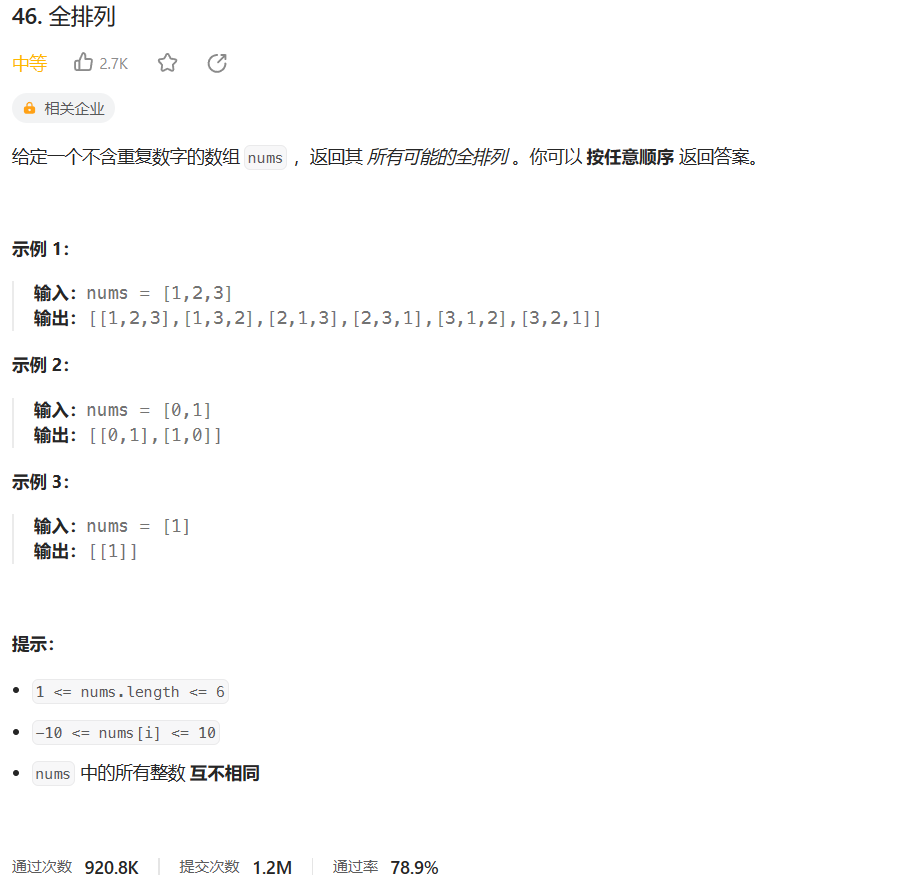
这题中nums中的数各不相同，所以不需要去重：
而下面这题，nums中的数会存在重复值，就需要去重：

方法一：递归+回溯

关键在于递归之后还要还原做回溯动作：

	path.add(nums[i]);//加入子结果集
    usered[i] = true;//将该位置标志位标为true  往下不能取了
    backtrace(nums,path,usered);//往下面继续递归
    usered[i] = false;//某次递归结束后，要回溯回去，就得把之前该的标志位还原
    path.remove(path.size()-1);//某次递归结束后，要回溯回去，当前path应该把递归之前加的元素给剔除掉

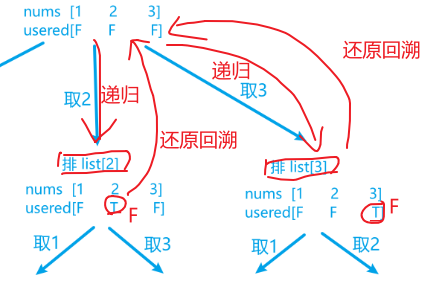
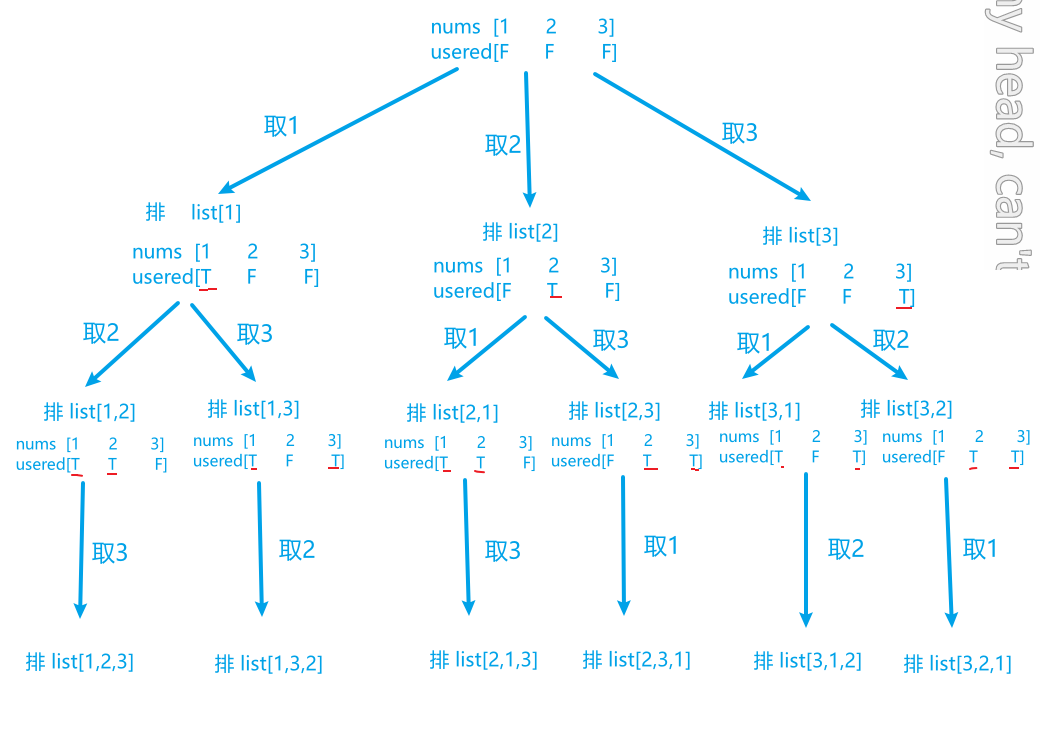
所以最后，我们统计到的res才是不断扩增结果集的，而usered标志数组和list子集合其实都是中间临时的，是会随着递归改变，并且随着回溯复原的，所以程序最后list子集合肯定是空的，并且标志数组也是初始化的时候的样子

所以在这句代码中的 res.add(new ArrayList<>(path))将子集合加入到结果集的时候就需要将满足条件的子结果集复制一份再放到最终结果集

      if(path.size() == nums.length) {//递归出口（子结果集大小 = 数组大小 ）
        res.add(new ArrayList<>(path));//因为path是实时变化的，必须要将path复制到一个新数组再放到res结果集
        return;
      }

如果我们这样做： res.add(path); ,直接将子结果集放到最终结果集，就会导致加入的子结果集为空，因为path子集合因为会做回溯操作 ，最后肯定加入的就是一个空数组，，满足条件的path只是一个中间状态。

class Solution {
    List<List<Integer>> res = new ArrayList<>();//最后的结果集
    public List<List<Integer>> permute(int[] nums) {
      List<Integer> path = new ArrayList<>(); //子结果集
      boolean[] usered = new boolean[nums.length]; //标记数组

      backtrace(nums,path,usered);

      return res;
    }

    public void backtrace(int[] nums ,List<Integer> path ,boolean[] usered){
      if(path.size() == nums.length) {//递归出口（子结果集大小 = 数组大小 ）
        res.add(new ArrayList<>(path));//因为path是实时变化的，必须要将path复制到一个新数组再放到res结果集
        return;
      }
      for(int i = 0 ; i < nums.length ; i++){
        if(usered[i]) continue;//如果标志位为true  则直接跳过
        else{
          path.add(nums[i]);//加入子结果集
          usered[i] = true;//将该位置标志位标为true  往下不能取了
          backtrace(nums,path,usered);//往下面继续递归
          usered[i] = false;//某次递归结束后，要回溯回去，就得把之前该的标志位还原
          path.remove(path.size()-1);//某次递归结束后，要回溯回去，当前path应该把递归之前加的元素给剔除掉
        }
      }

    }
}