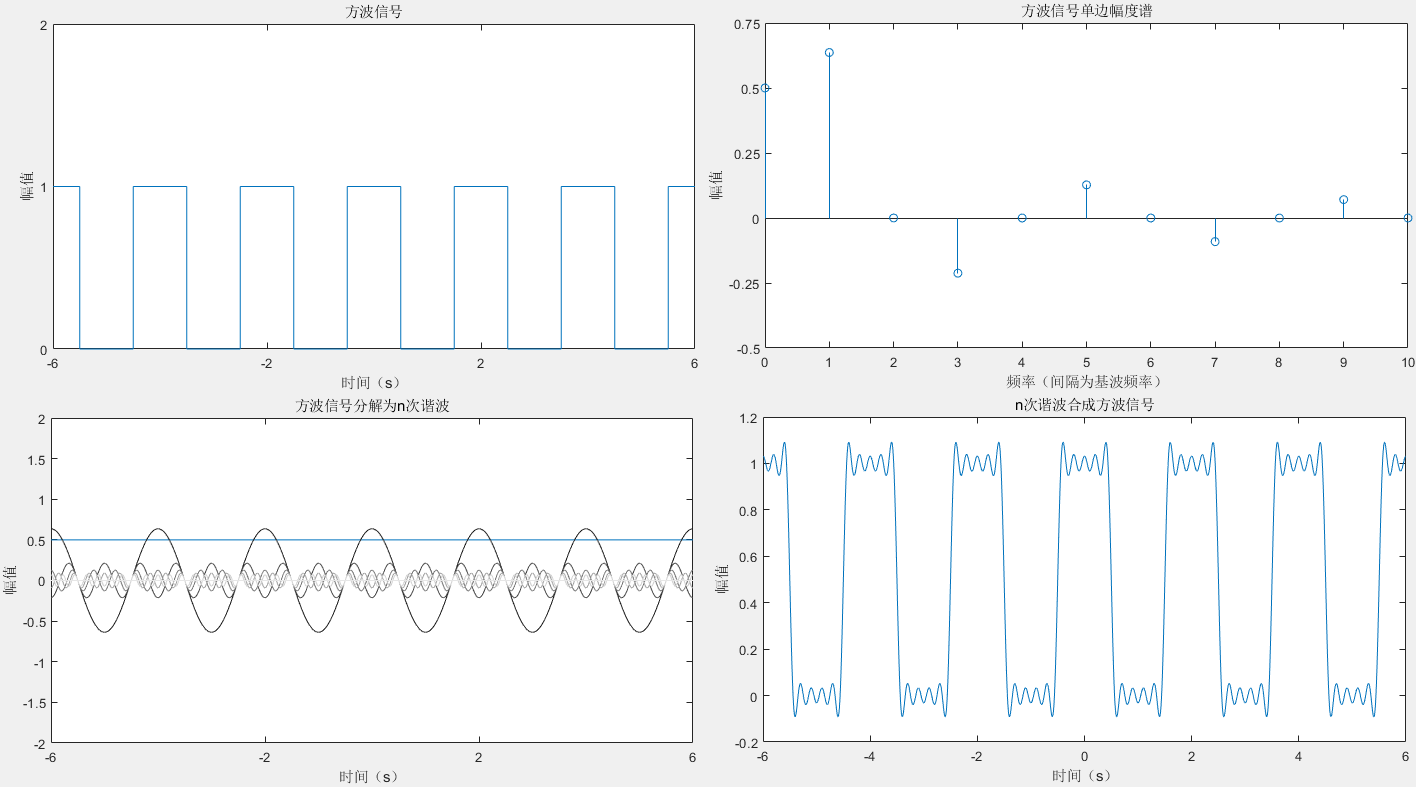
周期信号可展开为傅里叶级数，因此方波信号可用若干谐波去拟合。以下是Matlab的实现：

%% 方波信号的分解

% 1.生成方波信号
% 方波信号周期、基波频率
T0 = 2; w0 = (2 * pi) / T0;
% 方波信号值为1的区间
T1 = 0.5;
% 绘图周期：(2*n+1)个周期
n = 2.5;

% 方波信号时间范围、时间间隔
t = (-n*T0 - T0/2):0.001:(n*T0 + T0/2);
% 创建与t长度相同且其中所有元素都为0的一维向量y
y = zeros(1, length(t));
for i = 1:length(t)
    % 用以判断时间点是否落在幅值为0或1的区间
    t_ = mod(abs(t(1,i)),T0);
    % 方波信号赋值
    if(abs(t_)<T1||abs(t_)>T0-T1)
        y(1,i)=1; % 向量y中第1行第i列元素置1
    else
        y(1,i)=0;
    end
end

subplot(221);
plot(t,y);
xlim([(-n*T0 - T0/2) (n*T0 + T0/2)]);
ylim([0 2]);
set(gca, "XTick",(-n*T0 - T0/2):4:(n*T0 + T0/2));
set(gca,"YTick",0:1:2);
xlabel("时间（s）");
ylabel("幅值")
title("方波信号");

% 2.方波信号分解
% 直流分量系数
c0 = 2*T1/T0;
% 用以合成方波的谐波个数
num = 10;
% 各谐波的系数
ck=zeros(1,num);
for k = 1:num
    ck(1,k) = sin(k * w0 * T1) / (k * pi);
end

% 根据傅里叶级数的分解，绘制单边谱（傅里叶级数的余弦表达形式）
ck_cos = 2 * ck;
subplot(222);
stem(0:1:num, [c0 ck_cos]); % x轴坐标0~num，步长为1；y轴的值由后面向量给出
xlim([0 num]);
ylim([-0.5 0.75]);
set(gca,"XTick",0:floor(1):num); % x轴刻度步长1
set(gca,"YTick",-0.5:0.25:0.75);
xlabel("频率（间隔为基波频率）");
ylabel("幅值")
title("方波信号单边幅度谱");

% 绘制分解出的谐波图
% 绘制直流分量
subplot(223);
plot(t,c0*ones(1,length(t))); % ones是生成1行长度为length(t)的矩阵
hold on

% 绘制谐波分量
% 自动调整颜色
greylevel = 0.1:(0.9-0.1)/(num-1):0.9;

for k = 1:num
    plot(t,ck_cos(1,k)*cos(k*w0*t),"Color",[greylevel(1,k) greylevel(1,k),greylevel(1,k)]); % RGB
end

xlim([(-n*T0 - T0/2) (n*T0 + T0/2)]);
ylim([-2 2]);
set(gca,"XTick",(-n*T0 - T0/2):4:(n*T0 + T0/2));
set(gca,"YTick",-2:0.5:2);
xlabel("时间（s）");
ylabel("幅值");
title("方波信号分解为n次谐波");

% %图例
% str = [];
% str{1} = sprintf("直流分量");
% for i = 1:num
%     str{1+i} = sprintf("%d次谐波分量",i);
% end
% legend(str,"Location","NorthEastOutside");

% 3.n次谐波合成方波
subplot(224);
y_sum = c0*ones(1,length(t));
for i = 1:length(t)
    for k = 1:num
        y_sum(1,i) = y_sum(1,i) + ck_cos(1,k)*cos(k*w0*t(1,i));
    end
end

plot(t, y_sum);
xlim([(-n*T0 - T0/2) (n*T0 + T0/2)]);
xlabel("时间（s）");
ylabel("幅值");
title("n次谐波合成方波信号");

运行效果：