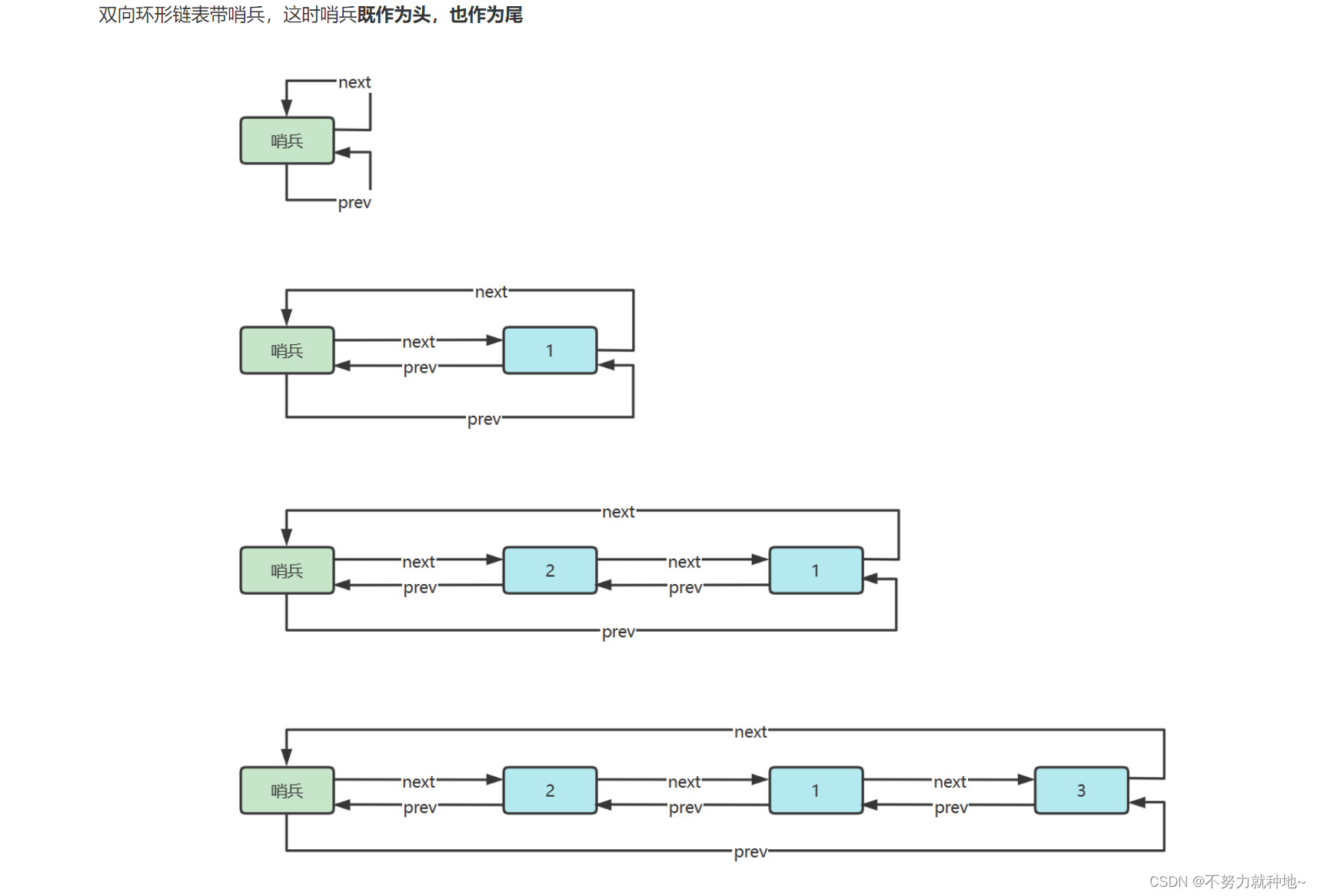
第三章

【3.1】

03、

• 假设以I和O分别表示入栈和出操作。栈的初态和终态均为空，入栈和出栈的操作序列可表示为仅由I和O组成的序列，可以操作的序列称为合法序列，否则称为非法序列。

  如IOIIOIOO 和IIIOOIOO是合法的，而IOOIOIIO和IIIOIOIO是不合法的。

  通过分析，写出一个算法，判定所给的操作序列是否合法。若合法，返回true，否则返回 false(假定被判定的操作序列已存入一维数组中)

个人理解：

就构造一个栈S，然后将这个序列进行处理，其中I表示入栈、O表示出栈，直接对栈S进行Push和Pop操作，有错误就报错，没错误就表示该序列合法，即可。

答案好像并没有创建栈，也没有执行Push、Pop的操作。而是直接对序列进行分析，只作了数学上的判定。

算法思想：

  扫描该序列，每扫描至任意一个位置均需检查出栈次数（即“O”的个数）是否小于等于入栈次数（“I”的个数），若大于则为非法序列。扫描结束后，再判断入栈和出栈次数是否相等，若不相等则也不合法。

bool Judge(char A[]) {
    int i=0;
    int j=0;	//j表示字母I的个数
    int k=0;	//k表示字母O的个数
    while(A[i]!='\0') {	//对字符串的遍历操作
        if(A[i]=='I')
            j++;
        if(A[i]=='O')
            k++;
        if(k>j) {
            printf("序列非法\n");
            return false;
        }
    }
    if(j!=k) {
        printf("序列非法\n");
        return false;
    }
    else {
        printf("序列合法\n");
        return true;
    }
    
}

另一种算法思想：

  入栈后，栈内元素个数增加1个；出栈后，栈内元素个数减少1个。因此可将判定一组出入栈序列是否合法转化为一组由+1和-1组成的序列，它的任意前缀子序列的累加和不能小于0（每执行一次出栈或入栈操作后立即判断）则合法，否则非法。此外，整个序列的累加和必须等于0。

思考：

  这个问题是否和括号匹配问题一样？——感觉好像是没啥区别。

04、

• 设单链表的表头指针为L，结点结构由data和next两个域构成，其中data域为字符型。试设计算法判断该链表的全部n个字符是否中心对称。

  例如xyx、xyyx都是中心对称。

个人理解：

第二章单链表部分的算法应该已经解决过这个问题了。

我大概有三种思路：

1）将单链表的后半段原地逆置，之后使用两个间距为k（k为表长的一半）的指针同步遍历比较。

分析：原地逆置但链表需要$O(n)$，两指针同步遍历需要$O(n)$。因此时间复杂度为$O(n)$，空间复杂度为$O(1)$。

2）把单链表中的元素复制到数组里，然后用数组直接判断中心对称。

分析：复制需要$O(n)$，数组判断中心对称需要$O(n)$。时间复杂度为$O(n)$，空间复杂度为$O(n)$。

3）从前往后把单链表中的各个结点元素依次入栈。之后将栈中元素一一出栈，并与单链表中从前往后元素进行比较。（如果知道链表的表长，只入栈前半个表的元素即可，一一出栈并与后半个表的元素比较）

分析：单链表元素一一入栈需要$O(n)$，一一出栈再进行比较需要$O(n)$。时间复杂度为$O(n)$，空间复杂度为$O(n)$。

05、

• 设有两个栈s1、s2都采用顺序栈方式，并共享一个存储区[0,...,maxsize-1]，为了尽量利用空间，减少溢出的可能，可采用栈顶相向、迎面增长的存储方式。试设计s1、s2有关入栈和出栈的操作算法。

个人理解：

就是考察共享栈的入栈、出栈具体操作上的细节。（不难，但是比较重要，各方面都要想清楚）

那就是栈s1初始栈顶指针为-1，栈s2初始栈顶指针为maxsize，对于两个栈而言，入栈操作都是先将指针移动一位（s1是往大了加1，s2是往小了减1的区别），然后再赋值。出栈操作反之，先取出当前栈顶指针的元素，然后栈顶指针移动一位（与入栈相反）。此外还有判断栈空、栈满的问题，栈空的问题好说，栈满的问题就是根据s2的栈顶指针是否和s1的栈顶指针相邻即可。

分析：

  两个栈共享向量空间，将两个栈的栈底设在向量两端。初始时，s1栈顶指针为-1，s2栈顶指针为maxsize。当两个栈顶指针相邻时判定为栈满。两个栈顶相向、迎面增长，栈顶指针指向栈顶元素。

【注意】

1）主要就是注意一下两个栈各自在入栈、出栈时，栈顶指针是如何变化的。对于s1而言，它是一个传统意义上的栈，而对于s2而言，它的操作大约是要反过来一下的。

2）对于所有入栈、出栈操作，都要时刻牢记**“入栈判满？出栈判空？”**的检查。

（0）如下定义共享栈的数据结构：

（当然，不这样定义，也无所谓。直接定义一个数组，然后定义两个变量指向栈顶位置也一样）

/* 共享栈的结构定义 */
#define maxsize 100
typedef struct {
    int stack[maxsize];		//栈空间
    int top[2];				//存放两个栈顶指针
}stk;

stk s;					//定义栈s为上述结构类型的变量，而且为全局变量
s.top[0] = -1;
s.top[1] = maxsize;		//初始化两个栈顶指针的值

（1）入栈操作

int push(int i, int x) {
    //入栈操作，i为栈号，当i=0时表示是s1执行入栈，当i=1时表示s2执行入栈
    //x是入栈元素
    //入栈成功返回1，失败返回0
    if(i<0 || i>1) {
        printf("栈号输入不对");
        exit(0);
    }
    if(s.top[1]-s.top[0] == 1) {
        printf("栈已满\n");
        return 0;
    }
    if(i==0) {
        s.stack[++s.top[0]] = x;
        return 1;
    }
    if(i==1) {
        s.stack[--s.top[1]] = x;
        return 1;
    }
}

（2）出栈操作

int pop(int i) {
    //出栈操作，i为栈号，当i=0时表示是s1执行出栈，当i=1时表示s2执行出栈
    //出栈成功，函数返回值为出栈的元素值；失败则返回-1
    if(i<0 || i>1) {
        printf("栈号输入错误");
        exit(0);
    }
    if(i==0) {
        if(s.top[0] == -1) {
            printf("栈s1已为空，无法出栈");
            return -1;
        } else
            return s.stack[s.top[0]--];
    }
    if(i==1) {
        if(s.top[1] == maxsize) {
            printf("栈s2已为空，无法出栈");
            return -1;
        } else 
            return s.stack[s.top[1]++];
    }
}

【3.2】

01、

• 若希望循环队列中的元素都能得到利用，则需设置一个标志域 tag，并以 tag 的值为0或1来区分队头指针 front 和队尾指针 rear 相同时的队列状态是“空”还是“满”试编写与此结构相应的入队和出队算法。

个人理解：

既然队空、队满的依据都是front==rear，只不过队空时tag==0，队满时tag==1。

那么，首先，队列为空时，初始化为tag=0，之后不断入队、出队操作。若最后一次操作执行入队，并使得队满，则tag=1；若最后一次操作执行出队，并使得队空，则tag=0。

咋样在队满的时候再检查一下上次操作的性质？——没必要。我们每次执行入队，都设tag=1，每次执行出队，都同时设tag=0，这样，如果发现front==rear了，同时就再去看看tag是几就行了。没那么复杂。

算法思想：

  在循环队列的类型结构中，增设一个tag的整型变量，进队时置tag为1，出队时置tag为0（因为只有入队操作可能导致队满，也只有出队操作可能导致队空）。队列Q初始时，置tag=0, front=rear=0。这样，队列的4要素如下：

队空条件：Q.front==Q.rear && Q.tag==0

队满条件：Q.front==Q.rear && Q.tag==1

进队操作：Q.data[Q.rear]=x; Q.rear=(Q.rear+1)%MaxSize; Q.tag=1

出队操作：x=Q.data[Q.rear]; Q.front=(Q.front+1)%MaxSize; Q.tag=0

1）入队算法

int EnQueue(SqQueue &Q, int x) {
    if(Q.front==Q.rear && Q.tag==1)
        return 0;		//队满
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear+1)%MaxSize;
    Q.tag = 1;		//可能队满
    return 1;
}

2）出队算法

int DeQueue(SqQueue &Q, int &x) {
    if(Q.front==Q.rear && Q.tag==0)
        return 0;		//队空
    x = Q.data[Q.front];
    Q.front = (Q.front+1)%MaxSize;
    Q.tag = 0;		//可能队空
    return 1;
}

02、

• Q 是一个队列，S 是一个空栈，实现将队列中的元素逆置的算法。

个人理解：

很简单了。队列元素依次出队，并依次入栈。最后栈中元素依次全部出栈即可。不是光输出元素值，那就再入回到队列中去。

算法思想：

  这个问题主要考察对于队列和栈的特性的理解。由于仅对队列进行一系列操作不可能将其中的元素逆置，而栈可以将入栈的元素逆序提取出来，因此我们可以让队列中的元素逐个地出队、入栈；全部入栈后再逐个出栈、入队列。

void Inverser(Stack &S, Queue &Q) {
    //本算法实现将队列中的元素逆置
    while(!QueueEmpty(Q)) {
        x = DeQueue(Q);		//队列中全部元素依次出队
        Push(S, x);			//元素依次入栈
    }
    while(!StackEmpty(S)) {
        Pop(S, x);		//栈中全部元素依次出栈
        EnQueue(Q, x);	//再入队
    }
}

03、

• 利用两个栈 S1 和 S2 来模拟一个队列，已知栈的 4 个运算定义如下：

Push(S, x);			//元素x入栈S
Pop(S, x);			//S出栈并将出栈的值赋给x
StackEmpty(S);		//判断栈是否为空
StackOverflow(S);	//判断栈是否满

如何利用栈的运算来实现该队列的 3 个运算（形参由读者根据要求自己设计）？

Enqueue;
Dequeue;
QueueEmpty;

有两个栈，S1和S2。两种栈的操作：入栈、出栈，此外还可以判栈空、判栈满。

以此来完成：入队、出队、判队空，的操作。

什么叫实现队列的入队、出队，就是，必须得是先进先出的运算逻辑才叫队列。

栈是后进先出的逻辑，怎么达到先进先出的效果？——两个栈配合使用。

让序列依次入栈到S1中，例如abcd进入S1：[a b c d]

此时S1出栈，肯定是d c b a，这肯定达不到队列的要求；但是可以把S1的出栈序列再次入栈到S2中，进入S2：[d c b a]。之后S2再出栈，就能得到a b c d。从而达到队列的效果。

但是好像有个问题：如果是一个元素、一个元素的这样操作的话，例如把a入栈S1后，立马出栈，再入栈到S2中，这样，元素a和直接入栈没区别，最后也不是队列的效果。必须一次性把所需序列全部入栈S1、再出栈S1、再入栈到S2中，才有效果。但是对于单个元素、单个元素这种的，就不能这样做。

看下答案怎么说。

算法思想：

  利用两个栈 S1 和 S2 来模拟一个队列，当需要向队列中插入一个元素时，用 S1 来存放已输入的元素，即 S1 执行入栈操作。当需要出队时，则对S2执行出栈操作；注意，此时需要判断S2是否为空，若为空，则需要将S1先出栈并入栈到S2；若S2不为空则直接执行S2出栈即可。总结如下两点：

（主要要搞清楚到底啥叫出队，啥叫入队。不是说入队就是abc进入，出队就是cba出来。入队、出队都只是一个元素的事。）

1）对S2的出栈操作，用作出队。若S2为空，则先将S1中的所有元素送入S2。

2）对S1的入栈操作，用作入队。若S1满，必须先保证S2为空，才能将S1中的元素全部插入S2中。

入队算法：

int EnQueue(Stack &S1, Stack &S2, int e) {
    if(!StackOverflow(S1)) {
        Push(S1, e);
        return 1;
    }
    if(StackOverflow(S1) && !StackEmpty(S2)) {
        printf("队列满");
        return 0;
    }
    if(StackOverflow(S1) && StackEmpty(S2)) {
        while(!StackEmpty(S1)) {
            Pop(S1, x);
            Push(S2, x);
        }
    }
    Push(S1, e);
    return 1;
}

出队算法：

void DeQueue(Stack &S1, Stack &S2, int &x) {
    if(!StackEmpty(S2))
        Pop(S2, x);
    else if(StackEmpty(S1))
        printf("队列为空");		//S2为空，此时去S1找，发现S1也为空
    else {
        while(!StackEmpty(S1)) {	//S2为空，如果S1里有，就先运过来
            Pop(S1, x);
            Push(S2, x);
        }
        Pop(S2, x);		//都运过来之后，S2出栈一下
    }
}

判断队列为空的算法：

int QueueEmpty(Stack S1, Stack S2) {
    if(StackEmpty(S1) && StackEmpty(S2))
        return 1;
    else
        return 0;
}

04、

[2019 统考真题]

• 请设计一个队列，要求满足：①初始时队列为空；②入队时，允许增加队列占用空间；③出队后，出队元素所占用的空间可重复使用，即整个队列所占用的空间只增不减；④入队操作和出队操作的时间复杂度始终保持为 0(1)。请回答下列问题：

  1）该队列是应选择链式存储结构，还是应选择顺序存储结构？

  2）画出队列的初始状态，并给出判断队空和队满的条件。

  3）画出第一个元素入队后的队列状态。

  4）给出入队操作和出队操作的基本过程。

根据题意，应该是要使用链式队列。主要是因为入队时允许增加队列占用空间这一点。如果是顺序存储空间会比较难实现。链表若想增加空间，则插入一个新结点即可。

此外，由于出队元素所占空间可以重复使用，因此应该还是个循环队列。

对于单链表存放队列而言，通常单链表表头对应的是队头，单链表表尾对应的是队尾。可知，出队操作在队头完成，入队操作在队尾完成。

综上，大概使用一个循环单链表（可以带上一个头结点，效果更好了），作为该循环队列的链式存储结构即可实现题目要求。

个人理解：

1）应选择链式存储结构。而且选用带头、尾指针的循环单链表比较合适。

2）初始状态为仅有一个头结点L，此时Q->front=Q->rear=NULL。队空判断条件为Q->front == Q->rear；队满判断条件为Q->rear->next = Q->front。

3）含有一个头结点、一个成员结点的循环单链表。

4）入队操作：若队列未满，则尾指针后移一位、元素赋值到尾指针所指结点上；若队列已满，则建立一个新结点，将新结点插入到尾指针后面。

出队操作：若队列非空，则输出头指针所指元素，并将头指针后移一位。若队列已经为空，则无法出队。

下面看下答案。

答案：

1）采用链式存储结构，循环单链表，即可满足四点要求。而顺序存储结构无法满足要求②。

2）可以参考循环队列的思维。不过此处由于是链式存储，因此入队时空间不够还可以动态增加。同样地，循环链式队列也要区分队满、队空的情况，这里参考循环队列牺牲一个存储单元的思想来做分析。初始时，创建只有一个空闲结点的循环单链表，头指针front和尾指针rear均指向空闲节点，如下图所示。

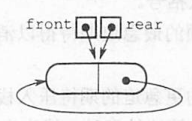
队空的判定条件：front == rear

队满的判定条件：front == rear->next

不要用死板的眼光看待问题。看这里可能会觉得：现在不是“队空”吗，什么也没有，而此时front == rear->next啊，这队空和队满怎么判定条件一样？

人家这就是队满。现在队列的实际空间为0，若想要入队一个元素，那就是队满的情形。同时，若想要出队一个元素，那就是队空的情形。

这个地方，链式队列要和顺序循环队列区分清楚，不要混为一谈。

3）插入第一个元素后的状态如下图所示：

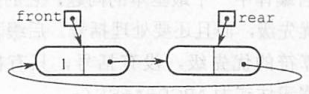
个人认为就在头结点的后面做头插即可。

4）操作的基本过程：

（他这个操作是根据他第（3）问画的图那样来弄的；如果画的图不一样，操作相应也有区别）

1.入队操作

若(front == rear->next)					//队满
	则 在rear后面插入一个新的空闲结点;
入队元素保存到rear所指结点中;
rear = rear->next;
return;

2.出队操作

若(front == rear)			//队空
	则 出队失败，返回;
取 front所指结点中的元素e;
front = front->next;
return e;