https://www.luogu.com.cn/problem/P4721
已知
g
g
g,求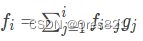
考虑分治,现在在 [ l , r ] [l,r] [l,r],先计算 [ l , m i d ] [l, mid] [l,mid],然后计算 [ l , m i d ] [l, mid] [l,mid] 对 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的贡献。
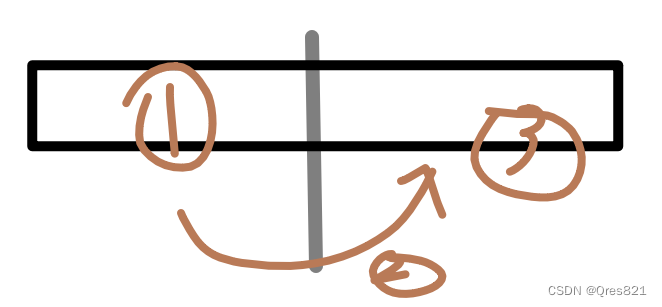
计算左对右的贡献,就把左边的 f f f 拿出来,乘上 g g g,贡献到右边的 f f f 里面。
和普通dp的计算类似,只不过贡献变成了NTT而已。
void solve(int l, int r, int logn) { //[l, r]
if(!logn) return ;
int mid=(l+r)>>1;
solve(l, mid, logn-1);
int i, j;
for(i=0, j=l; j<=mid; ++i, ++j) a[i]=f[j]; // 取出左边的f
for(; i<=(1<<logn); ++i) a[i]=0;
for(i=0; i<=(1<<logn); ++i) b[i]=g[i]; //拿出g
revese(r-l+1, logn);
NTT(a, r-l+1, 1); NTT(b, r-l+1, 1);
for(i=0; i<r-l+1; ++i) a[i]=a[i]*b[i]%mo; //计算f*g
NTT(a, r-l+1, -1);
for(i=mid+1, j=mid-l+1; i<=r; ++i, ++j)
f[i]=(f[i]+a[j])%mo; //贡献到右边
solve(mid+1, r, logn-1);
}






![【java】【项目实战】[外卖九]项目优化(缓存)](https://img-blog.csdnimg.cn/3dd4b4f783c043d0b9a6091f1b91eeb1.png)