目录

1 矩阵的秩

矩阵的秩

2 求秩的方法

矩阵的维度=秩

矩阵的维度

向量的模，矩阵的模-没有把，难道是面积？

矩阵的平直概念

5 矩阵的初等变换（矩阵等价概念的引出）

---

0 问题引出：什么是秩？

• 其实看线代一直挺模糊的，对这个概念，感觉好像就是维度，但好像又不是
• 更不清楚，为什么有了维度为啥要搞出一个秩的概念。
• 一般大家初步的想法就是，向量，矩阵/向量组不都有维度吗？
• 秩和维度什么关系？秩=维度吗？

概念备注：下面把向量=数组， 向量组=矩阵，这2组概念混用。

本文里

• 向量=数组
• 向量组=矩阵

1 什么是维数？

维数:维度的数量

讨论维度，首先需要明确对象：谁的维度？

• 向量的维度
• 向量组的维度
• 向量空间的维度
• 真实世界得维度

1.1 向量的维度

1. 列向量：α1  =[a11,a12......a1m]
2. 行向量：α1T=[a11,a12......a1m]T
3. 向量的维数，就是向量的分量的个数，比如α1  =[a11,a12......a1m] 有m个分量，维度就是m

1.2 向量组/矩阵的维度

向量α1=[a11,a12......a1m]

向量α2=[a21,a22......a2m]

....

因为向量组（矩阵）A=[α1, α2.......αn]

向量组是什么？向量组其实就是矩阵

1. 如果用row column分别表示行和列
2. 向量组可以转化为列向量组，比如[c1,c2.....cn]
3. 向量组可以转化为行向量组，比如[r1,r2.....rn]
4. 向量组的维度就得分别指，列向量组的维度 或 行向量组的维度

1.3 向量空间的维度

• 向量空间，就是一组最大线性无关的向量组/基 张成的空间

1. 一组最大线性无关的向量组=基
2. 一组最新线性无关的向量组/基 张成的空间，是指这些这个向量空间内的所有向量，都可以由这组线性无关的向量组，线性变换而成。

• 向量空间的维度，并不等于其中向量组/矩阵看起来的维度

1. 向量空间内的某些向量组（如列向量组），组成的维度可能<=向量空间的维度。
2. 向量空间内的某些向量组（如列向量组），组成的维度不可能超过向量空间的维度（否则就违背了空间的封闭性原则）
3. 向量空间内的某些向量组（如列向量组），组成的维度可能看起来大于向量空间的维度，但是实际上因为这些向量组之间是线性相关的，实际的维度并不会大于向量的维度。

1.4 真实世界的维度

• 0维空间：点
• 1维空间：一条线：直线/曲线。但强调是1条线！
• 2维空间：一个面：平面/曲面。但强调是1个面！
• 3维空间：立体图形，3维世界
• 4维空间：加时间，加啥的各种说法都有。。。。

1.1 维度的定义

我经常搞混高等代数里的各种秩和维数，可以帮我梳理一下不同数学对象的秩和维数的区别和联系吗？ - 知乎维数与秩是两件事，维数是指一个数组(学名向量)里面含有几个数字，每一个数字占据一个维度，数字越多，说…https://www.zhihu.com/question/503134151/answer/2256555187

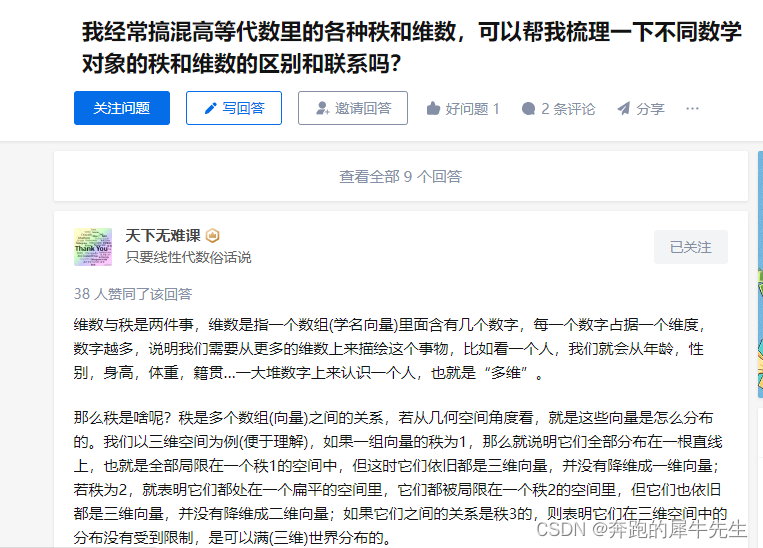
向量的维数是指：向量在分量的个数
如：（a,b,c）这就是一个三维向量.
但楼上说的对应一个超大空间说明没有理解
向量维数与空间维数的区别
所谓空间维数指的是空间基当中向量的个数,并不是由向量的维数确定的.
如｛x|x=k(a,b,c),k为任意常数｝这就是一维向量空间.就是空间当中的一条直线.

向量维数是表示向量有多少个分量，如（a，b，c）这就是一个三维向量，在数学中，向量（也称为欧几里得向量，几何向量，矢量），指具有大小（magnitude）和方向的量。

它可以形象化地表示为带箭头的线段。箭头所指代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫作数量（物理学中称标量）。

向量组的个数

向量组的个数，有2种数的方式

1.1 维度的定义

1.2 向量的维度

1.3 向量组的维度

区分概率

向量的维度和空间的维度

向量也可以看成是n*1的矩阵，或者1*n 的矩阵

为什么有秩这个概念

秩就是维度

 

为什么要引入矩阵的秩这一概念？ - 知乎一个n维空间的维数是n，它的任何一个局部的空间(子空间)的维数也是n，但一个局部空间的秩就不一定是n了，…https://www.zhihu.com/question/265684815/answer/2051914057

向量α1=[a11,a12......a1m]

向量α2=[a21,a22......a2m]

....

因为向量组（矩阵）A=[α1, α2.......αn]

向量没有秩，只有维度

或者可以认为向量的维度永远是1

向量=[1,2,3.....n]

因为向量考虑2种表现方式

1 如果还是用向量空间的表现方式，不管是有几个维度，最终都可以表达为这样的一个点

2 或者按坐标系的方式，全标记在一个数组上，理论上整数互相都可以互相取倍数关系，

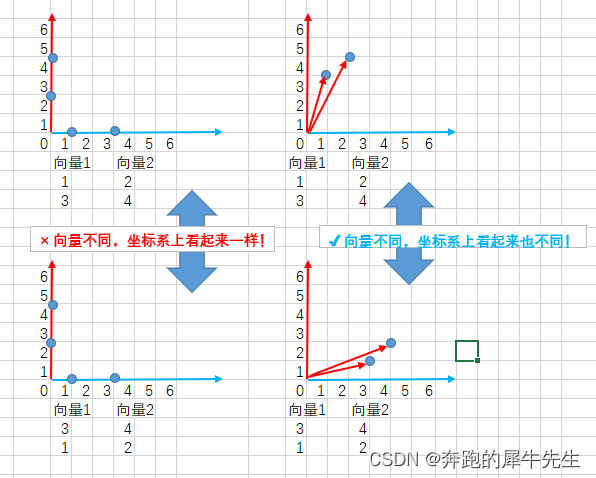
向量组才有秩

矩阵就是向量组

向量数量

最大无关组的向量数量

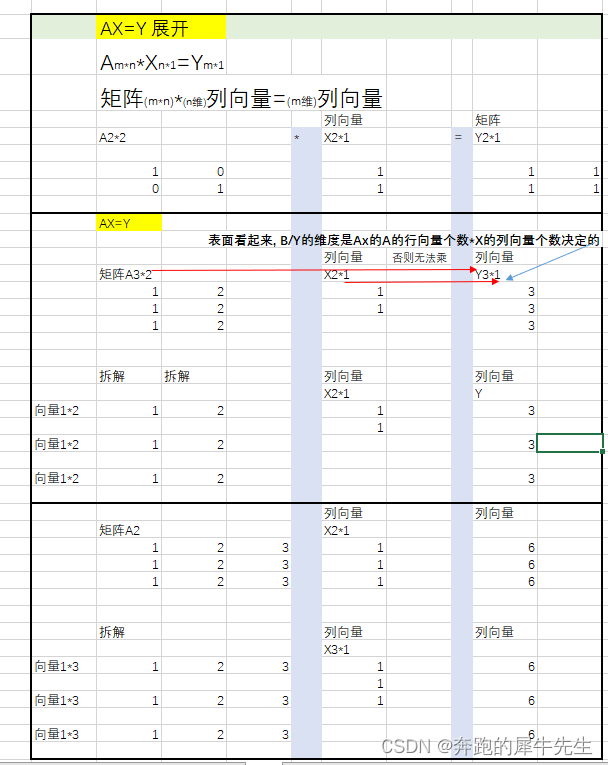
1 为什么要引入矩阵的“秩” 这个概念？先得从这样一个现象说起

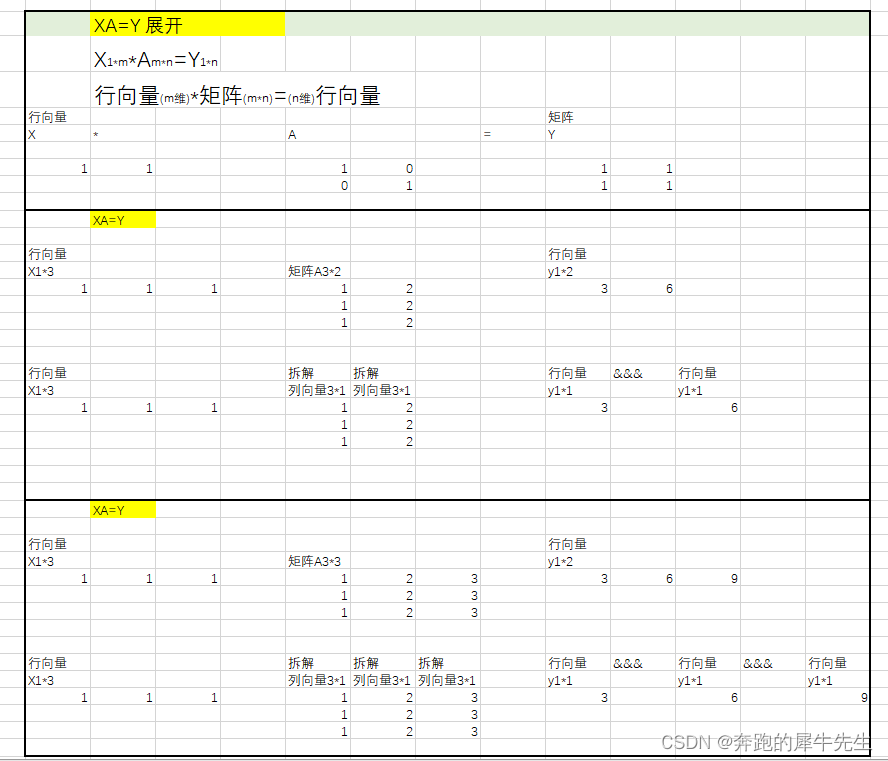
Ax=y

如果A是2维的向量/矩阵，定义域为维，那么输出的内容（值域）只能是0维，1维和2维

矩阵可以改变乘列向量组

• A={c1,c2....cn}
• c代表column
• 列秩=rank(colsp(A))

矩阵可以改变乘行向量组

• A={r1,r2....rn}
• r代表row
• 行秩=rank(rowsp(A))

定理1：矩阵的秩=列秩=行秩

• 因为 ：A的行秩 <= A的列秩 
• 因为 ：A的列秩 <= A的行秩 
• 所以 ：A的列秩 = A的行秩 

定理2

在自然定义域下，矩阵函数Ax=y的值域就是A的列空间

在自然定义域下，矩阵的秩 等于 矩阵函数Ax=y的值域的维度

定理3

如果某矩阵既是列满秩，又是行满秩，那么就称该矩阵为满秩矩阵，就简称满秩，。满秩矩阵必为方阵。

定理4

 rank(A) = rank(AT)

矩阵转秩后，行列空间互换，不会改变矩阵的秩

定理5 所有的初等行矩阵都是满秩矩阵

定理6，rank(AB)<=min(rank(A),rank(B))

rank(AB)<=rank(A)

rank(AB)<=rank(B)

定理7，假设P,Q为满秩矩阵，

rank(A)=rank(PA)=rank(AQ)=rank(PAQ)

定理8，假设A,B为 同型矩阵，  rank(A+B)<=rank(A)+rank(B)

定理9：对于矩阵函数来说，定义域是向量空间时，其值域也为向量空间，且，

定义域的维度>=值域的维度

定理10，当定义域是向量空间时，

有 矩阵函数是单射 等价于 定义域的维度=值域的维度

有 矩阵函数是非单射 等价于 定义域的维度>值域的维度

定理11 在自然定义域下，A是列满秩矩阵   等价  AX=y是单射

定理12 在自然定义域下，当矩阵是非单射时，值域中的每个向量都有无数定义域中的向量与之对应

定理13 在自然定义域下，A是行满秩矩阵   等价  AX=y是满射

定理14 在自然定义域下，A是满秩矩阵   等价  AX=y是双射

定理15 在自然定义域下，A是满秩矩阵   对应矩阵函数为双射，且A存在反函数，称为A可逆，

定理16，假设P,Q为满秩矩阵，

rank(A)=rank(PA)=rank(AQ)=rank(PAQ)
 

定理17，如果可以通过一系列初等变化矩阵Ei，讲A变成I，那么A的逆矩阵就是这些Ei的乘积

E1*E2*....A=I

18 如A可逆，那么A-也可以逆，(A-)-=A

定理24

1 矩阵的秩

行秩

列秩

满秩

矩阵的秩

• （a1,a2）是2维的
• （a1,a2,a3）是3维的
• （a1,a2,a3... ... an）是n维的

2 求秩的方法

行列式方法

线性变换方法

化简矩阵

3.2.3 秩的性质

满秩=有逆矩阵

矩阵的维度=秩

矩阵的维度

向量的模，矩阵的模-没有把，难道是面积？

矩阵的平直概念

即矩阵需要时线性增长的意思把

比如矩阵10，10个矩阵不能缩小为90，而必须是100

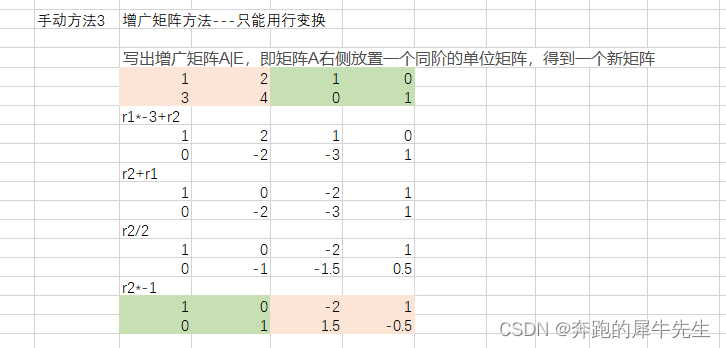
5 矩阵的初等变换（矩阵等价概念的引出）

• 如果两个矩阵，经过有限次的初等变化可以相等，那么这2个矩阵是等价的
• 矩阵的初等行变换与初等列变换合称为矩阵的初等变换。
• 矩阵的初等行变换

1. 交换矩阵的两行
2. 以一个非零数k乘矩阵的某一行所有元素
3. 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素

• 矩阵的初等列变换

1. 交换矩阵的两列
2. 以一个非零数k乘矩阵的某一列所有元素
3. 把矩阵的某一列所有元素乘以一个数k后加到另一列对应的元素

向量的变换，两种方法

基不变，会改变坐标（同时形状也可能改变）

基便哈/替代了，坐标不变（同时形状也不能改变）