VPG算法

前言

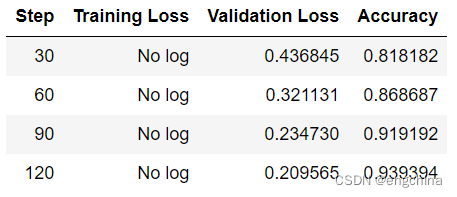
首先来看经典的策略梯度REINFORCE算法：

在REINFORCE中，每次采集一个episode的轨迹，计算每一步动作的回报$G_t$，与动作概率对数相乘，作为误差反向传播，有以下几个特点：

• 每个时间步更新一次参数
• 只有策略网络，没有价值网络
• 计算$G$时，仅仅采样了一条轨迹
• 一般来说，计算$G$时，从最后的时间步开始往前计算，这是为了节省计算量
• $G$实际上类似于$Q$函数，因为$Q$函数就是动作价值回报的期望

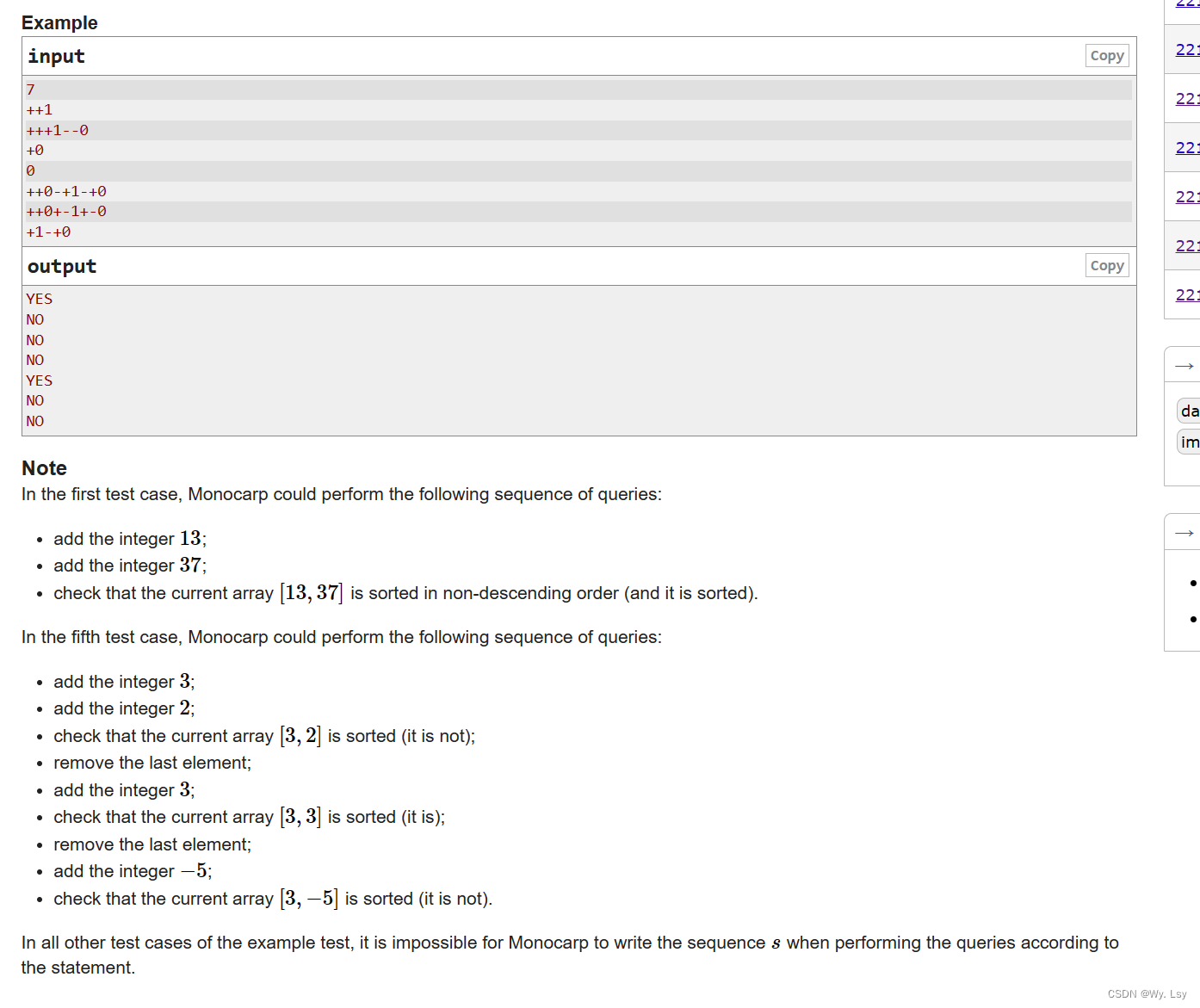
VPG算法

全称：Vanilla Policy Gradient，但是属于Actor-Critic算法，因为它既有策略网络，又有价值网络

• 每个episode更新一次参数
• 上述伪代码中，计算$G$时，采样了多个轨迹
• 一般来说，计算$G$时，从最后的时间步开始往前计算，这是为了节省计算量
• Reward-to-go：即折扣因子$\gamma =1$，$G_t={\hat{R}}_t=r_t+r_{t+1}+\dots +r_T$，$T$为episode的长度
• 通常为${\hat{A}}_t$引入baseline，以减小方差，提升训练稳定性

$${\hat{A}}_t={\hat{R}}_t-V_{{\varphi }_k}$$

比较

/	REINFORCE	VPG
价值网络	无	有
参数更新	每个时间步	每个episode
回报	有折扣	无折扣
采样轨迹	一条	多条
baseline	无	有