在组合数学中,卡特兰数是一系列自然数,出现在各种组合计数问题中,通常涉及递归定义的对象。它们以比利时数学家尤金·查尔斯·卡特兰(Eugène Charles Catalan)的名字命名。
卡特兰数序列是1, 1, 2, 5, 14, 42......(n = 0,1,...)。
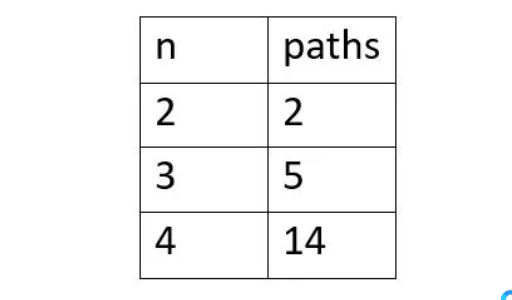
一般来说,用二项式系数表示的第n个卡特兰数如下:
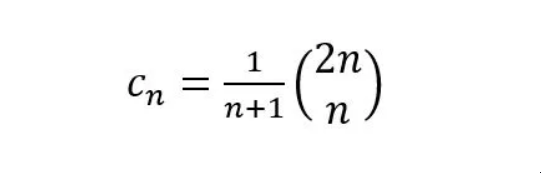
这也可以表示为:
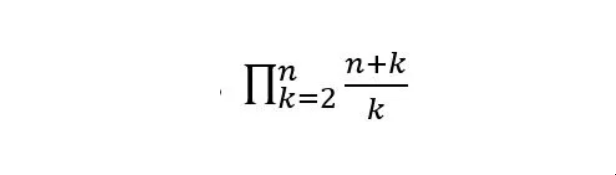
卡特兰数的奇特属性
如果使用卡特兰数形成矩阵如下所示:
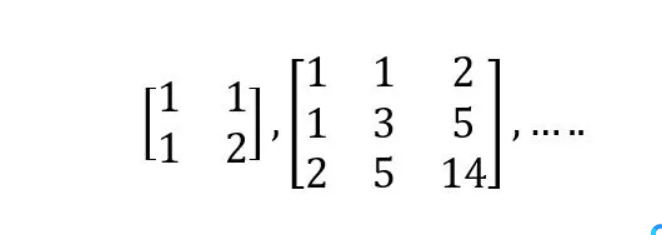
那么所有这些矩阵的行列式都将等于1。
卡特兰数在组合数学中的一些应用
格路径(Lattice Paths)
考虑一个平面,将其划分为边长为一单位的正方形方块,如下图所示。让点O作为原点(0,0),点P为任意点(n, n)。
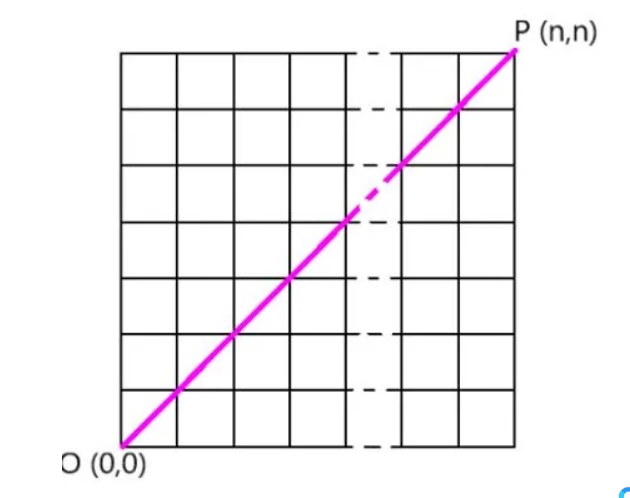
找出从O到P的路径数量,使得每条路径在或者在连接O和P的直线上方(如图中粉色标示)。
在任何情况下,你只能一次向上或一次向右前进一步。
解:
假设n = 2,那么我们有O(0,0)和P(2,2)。
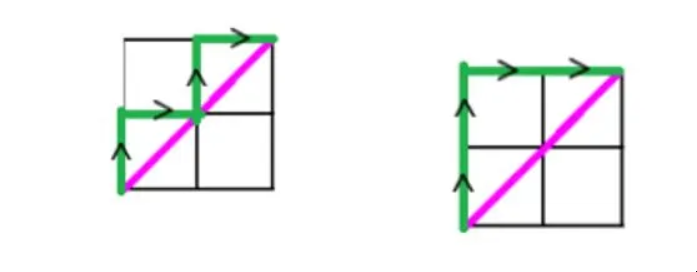
在这种情况下,我们可以有2条路径(绿色标示),如下所示:
类似地,对于n = 3,我们有O(0,0)和P(3,3)。
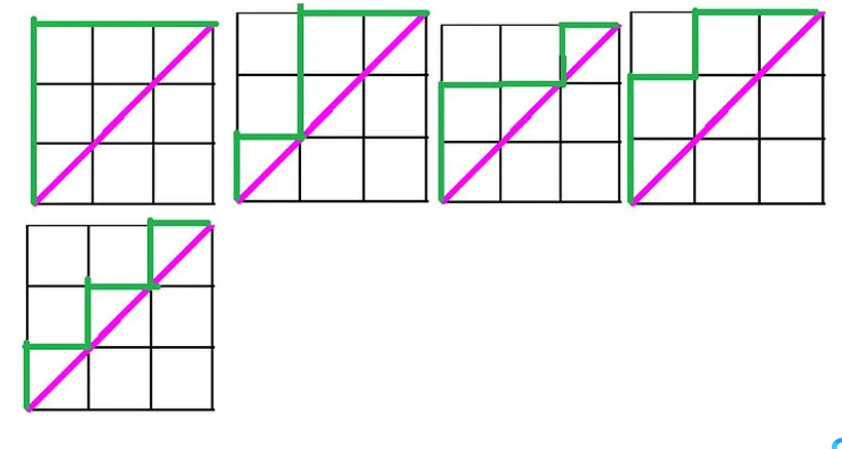
在这种情况下,我们可以有5条路径(绿色标示),如下所示:
同样,对于n = 4,我们可以有14条路径。
因此,我们有一个卡特兰数的序列。
一般的解决方案为n:
所需的路径数量(在粉色线上方或上面)=
(从O到P的总路径数) -(违反条件的路径数,即它们在粉色线下面)
假设路径没有限制,并考虑一般点Q(m, n),O为(0,0)。
用U表示向上步骤,用R表示向右步骤,为了从O到达点Q,我们需要m次向右和n次向上。这些步骤可以以任何方式进行。
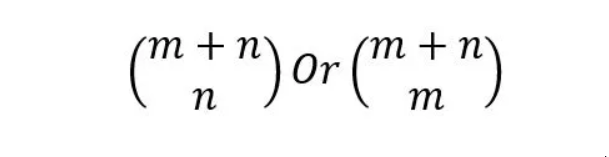
所以,我们需要排列m个R和n个U,可以用以下方式进行:
因此,从O到Q的总路径数由以下方式给出:

因此,从O(0,0)到P(n, n)的总路径数=
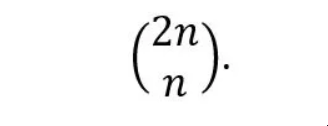
要找到违反路径的数量,我们使用反射技巧:
假设n = 4,即点P为(4,4),考虑任何违反路径,例如黄色线。
在第一个违反点X上标记一条与y = x平行的线(粉色线)。这条线以蓝色标示。
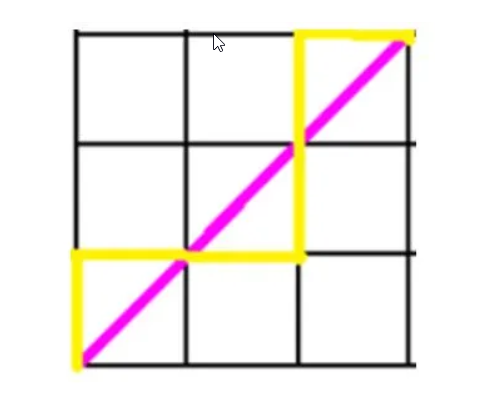
现在从点X绘制原始路径(黄色线)在与y = x平行的线(蓝色线)上的反射。这个反射路径用红色表示。将红色的终点标记为P'。
对于任何初始的违反路径,蓝色线都保持不变,因为所有第一个违反点都将在该线上。
在这种情况下,当n = 4时,遵循红色路径从X到达点P'(5,3)。

同样,对于n = 5,P'将是(6,4),对于n = 6,P'将是(7,5),依此类推。
一般来说,我们可以说点P'将是(n+1,n-1)。

显然,我们得到一个新的路径,它从(0,0)开始,以(n+1,n-1)结束。
这种给定黄色路径找到红色路径的过程是完全可逆的,即如果给定红色路径,我们可以找到黄色路径。
因此,从(0,0)到P的违反路径数量将等于从(0,0)到P'(n+1,n-1)的路径数量。
从(0,0)到P'(n+1,n-1)的路径数量(使用方程1)=
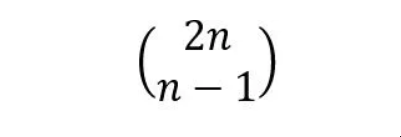
因此,违反条件的路径数量,即它们在粉色线下面 =。
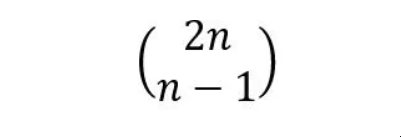
所需的路径数量(在粉色线上方或上面)=

这可以简化为
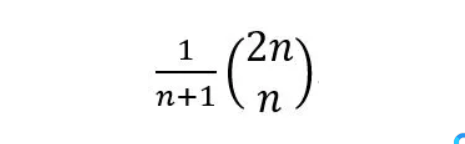
这就是第n个卡特兰数。
因此,粉色线上方和上面的路径数是卡特兰数。
(n+2)边正规多边形的三角形划分。
考虑一个(n+2)边的多边形,我们必须计算通过绘制其对角线将多边形划分为三角形的方式数量,使得没有两条对角线在多边形内部相交。
解:假设n = 2,我们有一个正方形。
如下图所示,我们可以以两种方式划分正方形:
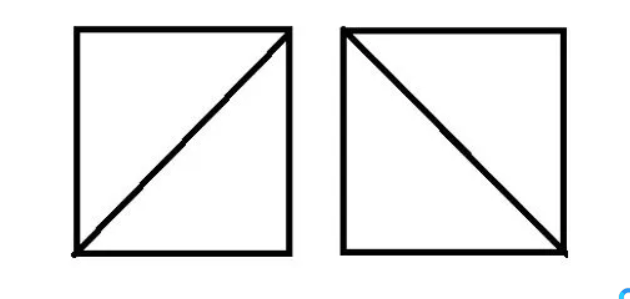
假设n = 3,我们有一个五边形。
如下图所示,我们可以以五种方式划分五边形:

同样,对于n = 4,我们得到六边形,我们可以以14种方式划分,依此类推。
这个序列也形成了一个卡特兰序列。

表达式加括号: 给定一个包含(n+1)项的表达式。我们需要找出如何加括号以使项的顺序不改变的方式数量。
解:为了简化起见,考虑给定操作为乘法。
假设n = 2,给定表达式为"abc"。
我们可以以2种方式加括号 -> (a(bc)),((ab)c)。
假设n = 3,给定表达式为"abcd"。
我们可以以5种方式加括号
(((ab)c)d),((ab)(cd)),((a(bc))d),(a((bc)d)),(a(b(cd)))
同样,对于n = 4,我们可以以14种方式进行,依此类推。

这个序列也形成了一个卡特兰序列。
握手问题:
有2n个人坐在圆形桌周围。找出他们可以互相握手的方式数量,使得手不交叉。握手只能用一只手,每个人一次只能与一人握手。
解:假设n = 2,我们有4人坐在桌旁。
这里的人以1、2、3、4表示,握手用一条线表示。

所以对于n = 2,我们可以有2种方式。
同样,对于n = 3,我们可以有5种握手的方式。
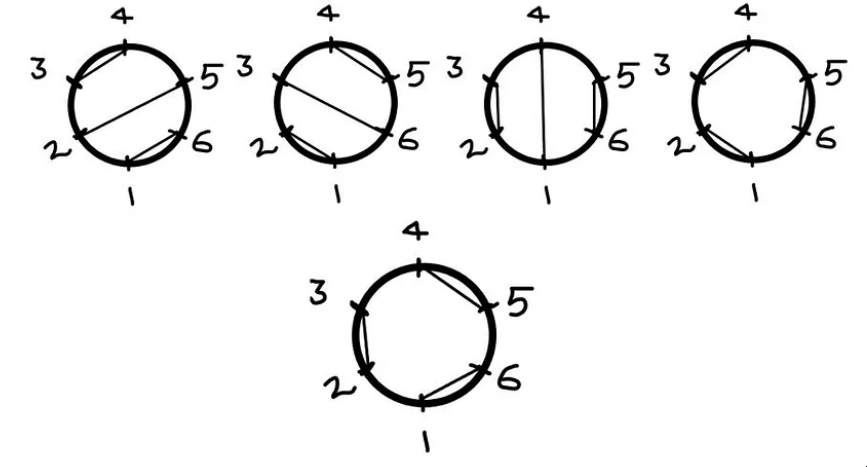
对于n = 4,有14种方式,以此类推。

这形成了一个卡特兰序列。
除了上面提到的应用外,这些卡特兰数在计算几何学、密码学和许多其他领域中还有许多应用。
我们可以在广泛的专业领域中找到这些数的用途,使它们成为最重要的整数序列之一。
卡特兰数算法是一种动态规划算法。
在组合数学中,卡特兰数形成了一系列自然数,出现在各种计数问题中,通常涉及递归定义的对象。
非负整数n上的卡特兰数是一组数字,在树的枚举问题中出现,问题类型是:“如果不同的方向被分别计数,那么一个正n边形可以以多少种方式分成n-2个三角形?”
卡特兰数算法的应用:
以平面上n个连续硬币组成底行的方式,其中不允许在底行两侧放置硬币,并且每个额外的硬币必须位于其他两个硬币的上方,这种堆叠硬币的方式数是第n个卡特兰数。
将一个包含n对括号的字符串分组的方式,使得每个开括号都有一个匹配的闭括号,这种分组的方式数是第n个卡特兰数。
在平面上将n+2边的凸多边形分割成三角形的方式,通过连接顶点与直线相交方式不相交,这种方式的数是第n个卡特兰数。这是欧拉感兴趣的应用。
使用以零为基础的编号,第n个卡特兰数可以通过以下方程直接表示为二项式系数的形式。
卡特兰数的示例: 这里n的值为4
辅助空间:O(n) 时间复杂度:O(n²)
卡特兰数的经典运用
卡特兰数(Catalan numbers)是一种组合数学中的数列,通常用Cn表示,其中n是一个非负整数。卡特兰数在许多组合数学和计算机科学问题中具有重要的应用。以下是一些卡特兰数的经典运用:
括号匹配问题:卡特兰数可用于描述括号匹配的不同方式。例如,n对括号的合法匹配方式的数量就是Cn。
二叉搜索树:卡特兰数可以表示n个节点的不同形态的二叉搜索树(BST)。这在计算机科学中用于分析算法的平均情况和性能很有用。
凸多边形的三角划分:给定一个n+2边的凸多边形,卡特兰数表示将其分成n个三角形的不同方式。这在计算几何学和图形学中很有用。
栈的操作序列:卡特兰数用于描述栈的不同操作序列的数量,如进栈和出栈的方式。
插入和删除操作的序列:在计算机科学中,卡特兰数用于表示插入和删除操作的序列的数量,如插入和删除字符以使括号匹配。
编程语言中的语法树:卡特兰数可用于计算不同语法树的数量,这在编译器设计和解析器生成中非常重要。
卡特兰数还在许多其他问题中发挥了重要作用,包括排列、组合、图形理论、密码学等等。
总之,卡特兰数是组合数学中的一个重要概念,它在各种领域中都有广泛的应用,帮助解决了许多与组合和计数相关的问题。
卡特兰数是一系列正整数,可以用于解决计算机科学中的各种问题。它们属于组合数学领域,与斐波那契数列一样,遵循一个基本的递归关系。它们还适用于动态规划方法。
本文将详细探讨这个主题,并将其应用于一些流行的计算机科学问题。与斐波那契数列一样,卡特兰数也遵循一种模式。序列中的前几个数字如下所示。
1, 1, 2, 5, 14, 42, 132, …
递归关系如下所示:
C3 = C0 * C2 + C1 * C1 + C2 * C0
可以从n = 2开始,基本情况为(C0 = C1 = 1),递归解决较小的子问题,逐步解决最终问题n。
与斐波那契数列类似,这也包含有重叠子问题,这使我们能够对子问题的答案进行备忘录化,以避免重复计算。
下面的代码使用递归和备忘录化来返回第n个卡特兰数。
def catalan_number(n, dp):
if n <= 1:
return 1
if dp[n] != -1:
return dp[n]
res = 0
for i in range(n):
res += catalan_number(i, dp) * catalan_number(n - 1 - i, dp)
dp[n] = res
return res
# 初始化备忘录
n = 10
dp = [-1] * (n + 1)
dp[0] = dp[1] = 1
result = catalan_number(n, dp)
print(f"The {n}-th Catalan Number is {result}")
以下是可以使用上述代码解决的一些问题:
具有n个节点的二叉搜索树的数量。 有效括号的数量。 具有某些递归关系修改的完全二叉树的数量。 具有高度h的完全二叉树的数量。 让我们详细了解如何将上述问题与卡特兰数序列相关联,以更好地理解它们的用途。
问题1:给定值n,返回构建具有n个节点的二叉搜索树的方式数量。
方法:
我们选择一个节点作为根节点。 我们遍历左子树和右子树中可以形成的节点组合。 我们将这些可能的组合相加,得到最终答案。
递归关系:
NWays(n) = NWays(0) * NWays(n-1-0) + NWays(1) * NWays(n-1-1) + ....NWays(n-1) * NWays(0)

问题2:给定值n,查找具有n对有效括号的可能组合数量。
方法:
就像上面的问题一样,我们选择1对括号作为默认值。 在默认括号周围,我们将计算所有可能的括号组合。 递归关系:与上述相同
( )()(), ( )(()), (())(), ((())) , (()())
问题3:给定值n,查找可以构建的可能完全二叉树数量。
方法:
与二叉搜索树问题不同,我们不能直接获取左子树和右子树中的所有节点组合。它们还必须满足完全二叉树的条件(每个节点具有0或正好2个子节点的树)。
根据定义,必须明确,无法构建具有偶数节点数的完全二叉树。
因此,我们需要更改第一个问题中的递归关系。 在这里,我们将遍历可以构建的左子树和右子树的有效组合。
递归关系:
如果(n为偶数) NWays(n) = 0 NWays(n) = NWays(1) * NWays(n-1-1) + NWays(3) * NWays(n-1-3) + ....NWays(n-1-1) * NWays(1)
注意,我们只使用奇数数量的节点来构建左子树和右子树。
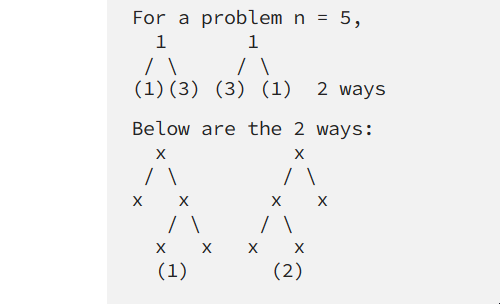
问题4:给定值n和值h,返回具有高度h的完全二叉树的构建方式数量。
方法:
在这个问题中,我们在第三个问题的状态中添加了一个参数。 这个参数代表所构建树的高度。
递归关系:
如果(n为偶数) NWays(n, h) = 0
NWays(n, h) = NWays(1, h-1) * NWays(n-1-1, h-1) + NWays(3, h-1) * NWays(n-1-3, h-1) + ....NWays(n-1-1, h-1) * NWays(1, h-1)
h-1是因为我们将根节点从高度中排除 其中h的范围从1到h。
NWays(n,h) - NWays(n, h-1)将给出我们构建高度h的完全二叉树的方式数量。
上述问题的基本情况是 NWays(0) = NWays(1) = NWays(1, 任何高度) = 1
希望这足够详细地描述了卡特兰数及其在计算机科学中的应用。谢谢!
本文由 mdnice 多平台发布

![一、了解[mysql]索引底层结构和算法](https://img-blog.csdnimg.cn/40b63e80d97b4e0caba8e68b4819bc98.png)