Problem - E - Codeforces

题意：

思路：

就是一个 N为1e5，M为3e5的背包问题，不过特殊条件是 w <= 3

我们去从最简单的情况开始考虑

当只有w = 1的物品和w = 2的物品时，考虑贪心地把物品按价值排序，然后选

这个非常的正确，然后加上w = 3的直接枚举即可

对于小数据的DP，我们可以尝试着这样设计：

 

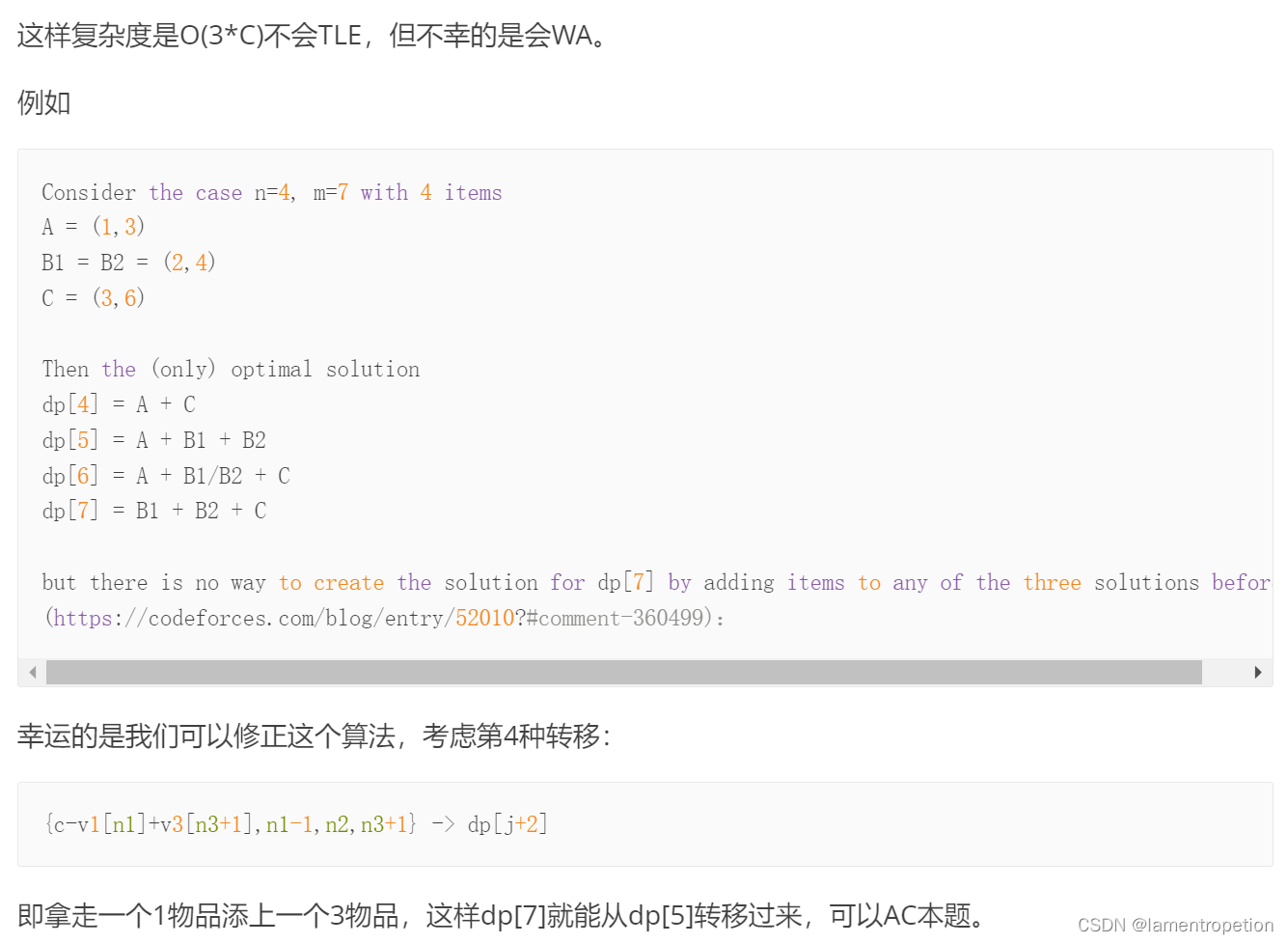
Code：

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 3e5 + 10;
constexpr int M = 3e5 + 10;
constexpr int P = 2600;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;

struct ty {
    int c, n1, n2, n3;
}dp[N];

std::vector<int> V[4];

int n, m;

void upd(ty &x, ty &y) {
    if (x.c < y.c) x = y;
}
void solve() {
    std::cin >> n >> m;
    
    for (int w = 1; w <= 3; w ++) {
        V[w].push_back(0);
    }

    for (int i = 1; i <= n; i ++) {
        int w, x;
        std::cin >> w >> x;
        V[w].push_back(x);
    }

    for (int w = 1; w <= 3; w ++) {
        std::sort(V[w].begin() + 1, V[w].end(), std::greater<int>());
    }

    int cnt1 = V[1].size() - 1;
    int cnt2 = V[2].size() - 1;
    int cnt3 = V[3].size() - 1;

    dp[0] = {0, 0, 0, 0};

    int ans = 0;
    for (int j = 0; j <= m; j ++) {
        int c = dp[j].c;
        int n1 = dp[j].n1;
        int n2 = dp[j].n2;
        int n3 = dp[j].n3;

        if (j + 1 <= m && n1 < cnt1) {
            ty t = {c + V[1][n1 + 1], n1 + 1, n2, n3};
            upd(dp[j + 1], t);
        }
        if (j + 2 <= m && n2 < cnt2) {
            ty t = {c + V[2][n2 + 1], n1, n2 + 1, n3};
            upd(dp[j + 2], t);
        }
        if (j + 3 <= m && n3 < cnt3) {
            ty t = {c + V[3][n3 + 1], n1, n2, n3 + 1};
            upd(dp[j + 3], t);
        }
        if (j + 2 <= m && n1 && n3 < cnt3) {
            ty t = {c - V[1][n1] + V[3][n3 + 1], n1 - 1, n2, n3 + 1};
            upd(dp[j + 2], t);
        }
        ans = std::max(ans, c);
    }

    std::cout << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;

    while (t--) {
        solve();
    }
    
    return 0;
}