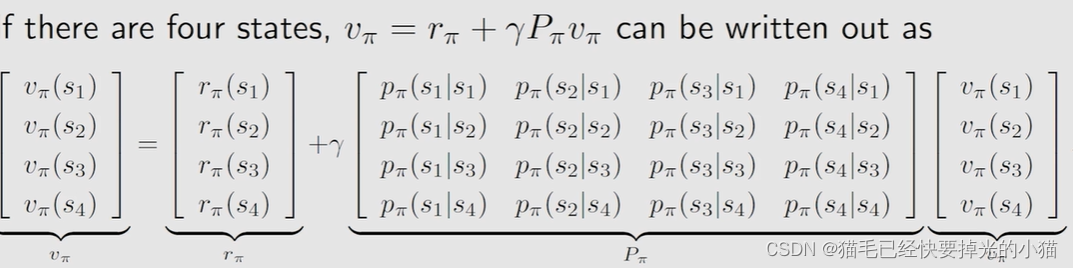【力扣】416. 分割等和子集＜动态规划、回溯＞

news2025/1/18 20:28:43

【力扣】416. 分割等和子集

给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：
1 <= nums.length <= 200
1 <= nums[i] <= 100

题解

动态规划

01背包问题：有 N 件物品和一个最多能背重量为 W 的背包。第 i 件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

背包的体积为sum / 2
背包要放入的商品（集合里的元素）重量为元素的数值，价值也为元素的数值
背包如果正好装满，说明找到了总和为 sum / 2 的子集
背包中每一个元素是不可重复放入

回溯五步：

确定dp数组以及下标的含义
01背包中，dp[j] 表示：容量为 j 的背包，所背的物品价值最大可以为 dp[j]
本题中每一个元素的数值既是重量，也是价值。
dp[j] 表示背包总容量（所能装的总重量）是 j，放进物品后，背的最大重量为 dp[j]
如果背包容量为 target， dp[target] 就是装满背包之后的重量，所以当 dp[target] == target 的时候，背包就装满了。
确定递推公式
01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
背包里放入数值，那么物品 i 的重量是 nums[i]，其价值也是 nums[i]。
所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
dp数组如何初始化
dp[j] 的定义来看，首先dp[0]一定是0，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。
确定遍历顺序
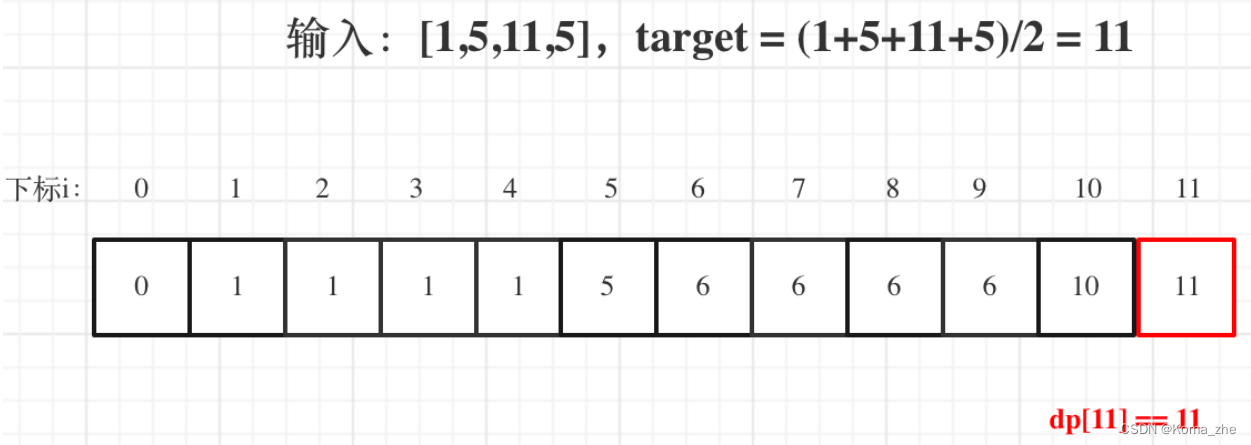
如果使用一维 dp数组，物品遍历的 for 循环放在外层，遍历背包的for循环放在内层，且内层 for 循环倒序遍历。
举例推导dp数组
dp[j] == j 说明，集合中的子集总和正好可以凑成总和 j

class B {
    public boolean canPartition(int[] nums) {
        if(nums == null || nums.length == 0) {
            return false;
        }
        int sum = 0;
        for(int num : nums) {
            sum += num;
        }
        //总和为奇数，不能平分
        if(sum % 2 != 0) {
            return false;
        }
        
        int target = sum / 2;
        int[] dp = new int[target + 1];
        
        for(int i = 0; i < nums.length; i++) {
            for(int j = target; j >= nums[i]; j--) {
                //物品 i 的重量是 nums[i]，其价值也是 nums[i]
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
            //剪枝一下，每一次完成內层的for-loop，立即检查是否dp[target] == target，优化时间复杂度（26ms -> 20ms）
            if(dp[target] == target)
                return true;
        }
        return dp[target] == target;
    }
}

回溯（会超时）

取与不取

class B {
    public static void main(String[] args) {
        B b = new B();
        int[] nums = {1,5,11,5};//true
//        int[] nums = {1,2,3,5};//false
        System.out.println(b.canPartition(nums));
    }

    // 回溯
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public boolean canPartition(int[] nums) {
        int target = 0;
        for (int i = 0; i < nums.length; i++) {
            target += nums[i];
        }
        if (target % 2 != 0) {
            return false;
        }

        target = target / 2;
        //Arrays.sort(nums);
        trace(nums, 0, target, 0);

        if (res.size() > 0) {
            // System.out.println(res);
            return true;
        } else {
            return false;
        }
    }

    public void trace(int[] nums, int start, int target, int sum) {
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }
        if (sum > target) {
            return;
        }
        for (int i = start; i < nums.length; i++) {
            path.add(nums[i]);
            sum += nums[i];
            trace(nums, i + 1, target, sum);
            sum -= nums[i];
            path.remove(path.size() - 1);
        }
    }
}