本文旨在讲解归并排序的实现（递归及非递归）搬好小板凳，干货来了！

---

 

前序：

在介绍归并排序之前，需要给大家介绍的是什么是归并，归并操作，也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法，相信不少小伙伴之前都做过合并两个有序链表或者两个有序数组的例题，归并就是将两个数组或链表合并成一个链表或数组，还得保证与其原来的顺序相同！那么归并排序就是用到了归并这个思想，将一组元素完成排序的算法！

---

归并排序的介绍 

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

---

归并排序的时间复杂度和空间复杂度

时间复杂度：O（N*logN），因为其是一种二叉树结构，其高度为logN,每层需要排序的个数都是N个，所以其时间复杂度为O（N*logN）。

空间复杂度：因为创建了一个新的数组，所以其空间复杂度为O（N）；

---

归并排序的思想与思路

归并排序就是本质上是分治的方法来实现的，是将一组数据分割成若干组有序数组，然后对这若干个有序数组两两进行归并即可得到我们想要的排序！

---

归并排序的思路图

---

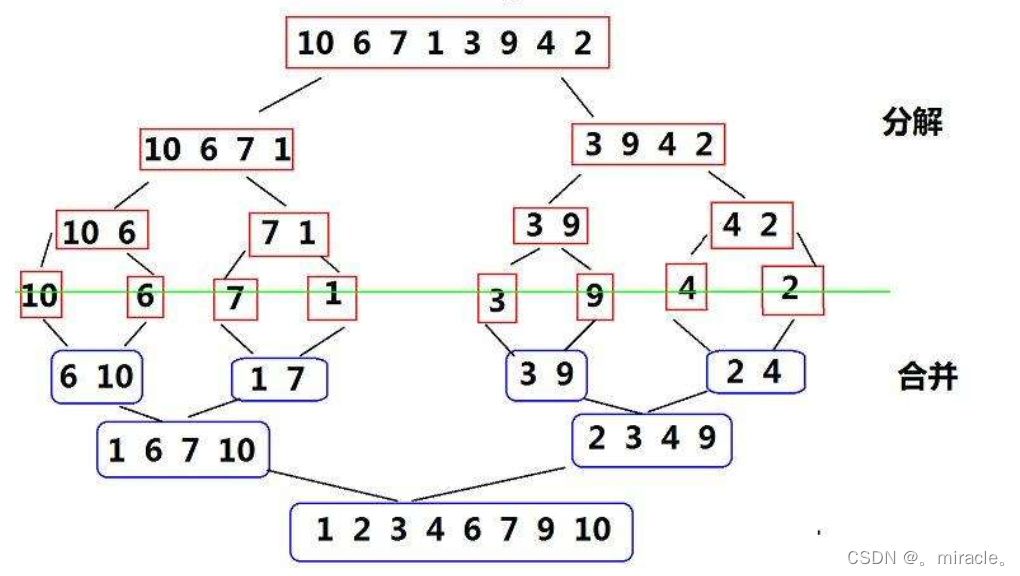
归并排序的动态图展示

---

归并排序的大致实现思路 

归并排序其实现的思路其实很简单，就是将一组数据分割，分割到若干组有序数组，然后两两进行归并，那么如何保证分割的数组为有序数组呢，这其实很简单，当分割到数组中只有一个元素的时候，那么该数组就是有序的数组了！然后进行归并拷贝到原数组上即可！

---

归并排序的代码实现

（C版本递归）

void _MergeSort(int* a, int left, int right, int* tem)
{
	//当再次需要调用的区间不存在时，返回即可！
	if (left == right)  //很显然，left不会大于right，保险起见，加上大于条件没有影响！
	{
		return;
	}
	//每次取出中间坐标，用于下次的左半边的递归，右半边递归同理！
	int mid = (left + right) / 2;
	_MergeSort(a, left, mid, tem);
	_MergeSort(a, mid + 1, right, tem);
	//到此，分割区间已经结束，每组区间都能保证时有序的了！下一步就开始进行归并！
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;  //i用于对tem数组的下标进行表示！
	//下面开始归并两个有序数组，当两个有序数组其中一个遍历完成就退出循环！
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tem[i++] = a[begin1++];
		}
		else
		{
			tem[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tem[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tem[i++] = a[begin2++];
	}

	//归并结束后，将tem数组中的数据，拷贝到元素组中相应的位置即可！
	memcpy(a + left, tem + left, sizeof(int)*(right - left + 1));//个数为右边界减去左边加1，因为为闭区间！
	//至此，归并结束，拷贝结束!
}
void MergeSort(int* a, int n)
{
	//在堆上申请开辟一个tem数组，用来最后拷贝到原数组中！
	int* tem = (int *)malloc(sizeof(int) * n);

	//因为存在递归的调用，所以再创建一个函数，若仍在此函数上重复调用时，则会重复开辟新的空间，可能导致空间不足！
	_MergeSort(a, 0, n - 1, tem);

	//用完之后释放到tem数组！
	free(tem);
}

需要注意的是：当进行递归归并排序的时候，需要注意返回的条件，当区间不存在或者区间内部只有一个元素的时候就可以返回了！还需要注意的是，因为要进行拷贝，不能在原数组上直接拷贝，所以需要创建一个新的数组用来存储归并后的元素的位置，最后归并结束重新拷贝到原数组中即可！

---

（C版本非递归）

分段拷贝

// 归并排序非递归实现

//思路如下：要想实现归并排序的非递归，那么需要注意分组，从每组一个元素开始，因为当只有一个元素的时候，默认是有序的，然后
//进行归并拷贝即可，每组一个元素遍历结束之后，进行每组两个，依次进行每组2倍个元素进行归并！，当每组的元素为所有元素的一半或大于一半，
//即可完成排序，需要特别注意的是，进行非递归归并排序的时候，需要注意区间的取值，在此有两个拷贝方式，一种是整体拷贝，一组是归并一段拷贝一段！


//进行非递归实现归并的时候也需要创建一个新的数组，不能在原数组上进行对数据的改变，因为可能会造成数据的覆盖，导致数据不能完成排序！
//创建一个新数组，然后让每组元素为一个依次递增二倍，进行归并拷贝，直至每组的元素个数大于数组个数结束归并即可完成排序！

//下面先来进行分段拷贝！
//void MergeSortNonR(int* a,int n)
//{
//	//注意：gap代表的是每组归并时的元素的个数！
//	int gap = 1;
//	int* tem = (int*)malloc(sizeof(int) * n);
//	while (gap < n)		//当gap大于n时结束循环即可完成！
//	{
//		int j = 0;
//		//每组为一个的进行遍历！
//		for (int i = 0; i <n ; i+=2*gap)
//		{
//
//			//每组个数为1的进行归并排序！
//			//区间范围如下!
//			int begin1 = i, end1 = i + gap - 1;
//			int begin2 = i + gap, end2 = i + 2 * gap - 1;
//
//			//当end1>n,begin2>n时，不需要进行归并！
//			if (end1 >= n||begin2>=n)
//			{
//				break;
//			}
//
//			//对end2边界进行修改！
//			if (end2 >= n)
//			{
//				end2 = n-1;
//			}
//			
//			//开始进行归并拷贝！
//			while (begin1 <= end1 && begin2 <= end2)
//			{
//				if (a[begin1] < a[begin2])
//				{
//					tem[j++] = a[begin1++];
//				}
//				else
//				{
//					tem[j++] = a[begin2++];
//				}
//			}
//			while (begin1 <= end1)
//			{
//				tem[j++] = a[begin1++];
//			}
//			while (begin2 <= end2)
//			{
//				tem[j++] = a[begin2++];
//			}
//
//			//注意：需要注意的是：当求元素的个数时，应该用end2-i,不能减去begin1，因为begin1每次都会改变，记录的不再是数组开始拷贝的地方！
//			memcpy(a + i, tem + i, sizeof(int) * (end2 - i + 1));
//		}
//		gap *= 2;
//	}
//	free(tem);
//}

整体拷贝

//整段拷贝！
void MergeSortNonR(int* a, int n)
{
	//注意：gap代表的是每组归并时的元素的个数！
	int gap = 1;
	int* tem = (int*)malloc(sizeof(int) * n);
	
	while (gap < n)		//当gap大于n时结束循环即可完成！
	{
		//j的声明必须写在for循环的外面，因为若写到for循环内部时，在每组循环都会将原来归并好的数据放到前面的那些位置
		//导致以及归并好的又被覆盖，导致排序失败！（每组的归并都放在前两组内部，导致不能将全部归并结束，！）
		int j = 0;
		
		//每组为一个的进行遍历！
		for (int i = 0; i < n; i += 2 * gap)
		{

			//每组个数为1的进行归并排序！
			//区间范围如下!
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//当end1>n,begin2>n时，不需要进行归并！
			if (end1 >= n)
			{
				end1 = n - 1;

				//将第二块区间设置为不存在的区间！如果设置为n-1那么会造成对最后一个数据的重复使用，拷贝，导致排序错误！
				begin2 = n;
				end2 = n - 1;
			}

			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if(end2>=n)
			{
				end2 = n - 1;
			}
			//开始进行归并拷贝！


			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tem[j++] = a[begin1++];
				}
				else
				{
					tem[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tem[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tem[j++] = a[begin2++];
			}

			//注意：需要注意的是：进行整段拷贝的时候，不需要再从a+begin1的位置开始拷贝啦，直接将所有tem中的元素拷贝到原数组即可！

		}

		memcpy(a, tem, sizeof(int) * n);
		gap *= 2;
	}

	free(tem);
}

需要注意的是：非递归的归并排序，整体拷贝和分段拷贝大致思路是一样的，只是最后进行memcpy的起始位置和个数有所不同！相关细节与思路都在源代码上加有注释标明，需要注意的是：当进行整体拷贝的时候，用于标记tem数组的j的坐标的定义一定要在for循环外部定义赋值，若在内部赋值定义，则每进行一次都会覆盖原来已经归并好的数据上面，导致归并排序不能正确进行！

今日的归并排序分享到此结束，欢迎大家积极评论支持。若有不足及补充，及时提出，必将改正！