1、颜色分类

颜色分类

在这里插入图片描述

其实这道题的做法是三指针。双指针思路中，定义两个指针，假设要把整个数组划分成a和b区间，ab区间的数有各自的特点，一个指针遍历整个数组，另一个指针指向a区间的最后一个元素位置。而三指针，也是同样的思路，三个指针，abc三个区间，一个指针仍然在遍历数组，但它不需要遍历完所有，一个指针指向a区间的最右侧，一个指针指向c区间的最左侧，这样三个区间也就能划分出来了。在实际操作中，会分出四个区间

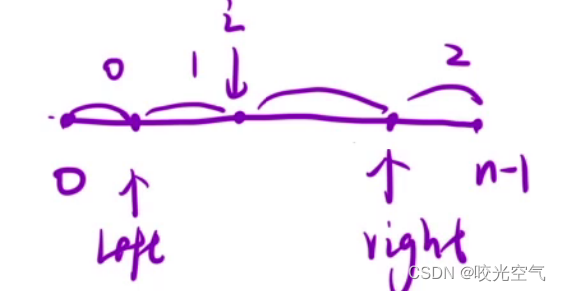
在这里插入图片描述

[0, left]全是0，[left + 1, i - 1]全是1，[i, right - 1]是待扫描的元素，[right, n - 1]全是2。

代码开始时，我们要如何做？left和right自然是在整个数组下标的0和n - 1处，i每次检测到数字，就去判断应该放到哪个区间，然后交换元素，把数字放到区间，left或者right移动，而i如果是放到left左边，i可以++，但是和right右边的元素交换后，i不能++，它还需要判断交换过来的数字。

    void sortColors(vector<int>& nums) {
        int n = nums.size();
        int i = 0, left = -1, right = n;//为什么要这么设置left和right1的值? 看下面的代码就能明白了
        while(i < right)//为什么要小于right？right到最后都是为2的元素，等到i和right重合时，其实就已经完成了整体的排序
        {
            if(nums[i] == 0)
            {
                swap(nums[++left], nums[i++]);
            }
            else if(nums[i] == 1)
            {
                i++;
            }
            else if(nums[i] == 2)
            {
                swap(nums[--right], nums[i]);
            }
        }
    }

2、排序数组

排序数组

在这里插入图片描述

其实这道题就是实现快排。我们要设置基准值key，把区间划分成两部分，<=key 和 >key，然后再到两个区间实现同样的操作，找key，划分区间。如果数组里都是重复元素的话，这个排序的复杂度就不好了。那么这里就把数组分三块的思想来实现快排，其实这个数组分三块的思路就是排序（2）那篇博客中的双指针法，思路都相似。我们要分成三个区间，< key = key > key，每次比较的时候就是交换，指针++等操作。

同上面一样

小于key：swap（nums[++left], nums[i++]）
等于key：i++
大于key：swap（nus[–right], nums[i]）

但是这里还有优化，上面时间复杂度是O(N)，想要达成N * logN，就必须要随机选取key值。而这里的随机也不是简单的随机，我们要让整个区间的数都能等概率地没取到，我们的做法就是rand() % (right - left + 1) + left，偏移量 + left得到对应的数值，这个得出来的值是数组的下标，也就是nums[rand() % (right - left + 1) + left]。

上代码

    vector<int> sortArray(vector<int>& nums) {
        srand(time(NULL));//开始随机，种下随机数种子
        qsort(nums, 0, nums.size() - 1);
        return nums;
    }

    void qsort(vector<int>& nums, int l, int r)
    {
        if(l >= r) return ;
        //数组分三块
        int key = getRandom(nums, l, r);
        int i = l, left = l - 1, right = r + 1;//这里就和上面的颜色分类的做法就一样了，也就是上面灰框中的实现
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right], nums[i]);
        }
        qsort(nums, l, left);
        qsort(nums, right, r);
    }

    int getRandom(vector<int>& nums, int left, int right)
    {
        int r = rand();
        return nums[r % (right - left + 1) + left];
    }

3、第k个最大的元素（快速选择）

数组中的第K个最大元素

在这里插入图片描述

TOP K有4种问题，第k大，第k小，前k大，前k小。之前的博客对此用的是堆排序的算法。还有另外一个就是快速选择算法。堆排是O(N*logN)，而快速选择是O(N)。

快速选择基于快排。整个区间左右端点为l和r，分成三个区间abc，三个区间内，我们需要确定第k大的数字在哪个区间内。假设abc就是每个区间的元素个数，如果在第三个区间，也就是>key的区间，那么c >=k；如果第一个条件不成立，那么如果在第二区间，那么b + c >=k，直接返回key就行，因为第二个区间都是=key的数字；如果上面两个条件都不成立，那么就去第一个区间找，找k - (b + c)大的数字。

    int findKthLargest(vector<int>& nums, int k) {
        /*priority_queue<int, vector<int>, greater<int>> pq(nums.begin(), nums.begin() + k);
        for(size_t i = k; i < nums.size(); ++i)
        {
            if(nums[i] > pq.top())
            {
                pq.pop();
                pq.push(nums[i]);
            }
        }
        return pq.top();*/
        //上面是用优先级队列解决的
        srand(time(NULL));
        return qsort(nums, 0, nums.size() - 1, k);
    }

    int qsort(vector<int>& nums, int l, int r, int k)
    {
        if(l == r) return nums[l];//必然存在至少一个元素，所以l不可能大于r
        //1. 随机选择基准元素
        int key = getRandom(nums, l, r);
        //2. 根据基准元素分三块
        int left = l - 1, right = r + 1, i = l;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right], nums[i]);
        }
        int c = r - right + 1;
        int b = right - left - 1;
        if(c >= k) return qsort(nums, right, r, k);
        else if(b + c >= k) return key;
        else return qsort(nums, l, left, k - b - c);
    }

    int getRandom(vector<int>& nums, int left, int right)
    {
        return [rand() % (right - left + 1) + left];
    }

4、最小的k个数（快速选择）

剑指 Offer 40. 最小的k个数

在这里插入图片描述

针对这样的问题，我们可以堆排序，也可以快速选择算法。堆排是N * logk，快速选择可以到达N。

还是l ，left， right， r，abc。如果a > k，那就在a区间找；条件不符合，那就去a + b >= k，那就返回key，因为第一个条件不符合，那么第二个条件符合的话，k一定就是在=key的区间，那就返回key；上述两种条件都不符合，那就得在c区间找。

对上一个稍作修改。

   vector<int> getLeastNumbers(vector<int>& arr, int k) {
        srand(time(NULL));
        qsort(arr, 0, arr.size() - 1, k);
        return {arr.begin(), arr.begin() + k};
    }


    void qsort(vector<int>& nums, int l, int r, int k)
    {
        if(l == r) return ;
        int key = getRandom(nums, l, r);
        int left = l - 1, right = r + 1, i = l;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right], nums[i]);
        }
        int a = left - l + 1;
        int b = right - left - 1;
        if(a > k) return qsort(nums, l, left, k);
        else if(b + a >= k) return ;
        else qsort(nums, right, r, k - b - a);
    }

    int getRandom(vector<int>& nums, int left, int right)
    {
        return nums[rand() % (right - left + 1) + left];
    }