文章目录
- 二叉树的定义
- 二叉树的遍历方式
- 前序遍历
- 递归DFS
- 迭代(栈)
- 中序遍历
- 递归DFS
- 迭代(栈)
- 后序遍历
- 递归DFS
- 迭代(栈)
- 层序遍历
- 迭代(队列)
二叉树的定义
二叉树是一种常见的树状数据结构,它由一个称为根节点(Root)的节点和最多两个指向其他节点的指针(左子节点和右子节点)组成。
static class TreeNode{
public char val;//节点值
public TreeNode left;//左孩子节点
public TreeNode right;//右孩子节点
public TreeNode(char val){//节点赋值
this.val = val;
}
public TreeNode(char val,TreeNode left,TreeNode right){//节点赋值的同时,指定左右孩子
this.val = val;
this.left =left;
this.right =right;
}
}
二叉树的遍历方式
- 创建二叉树:
public static TreeNode creatTree(){
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
return A;
}
图示为:
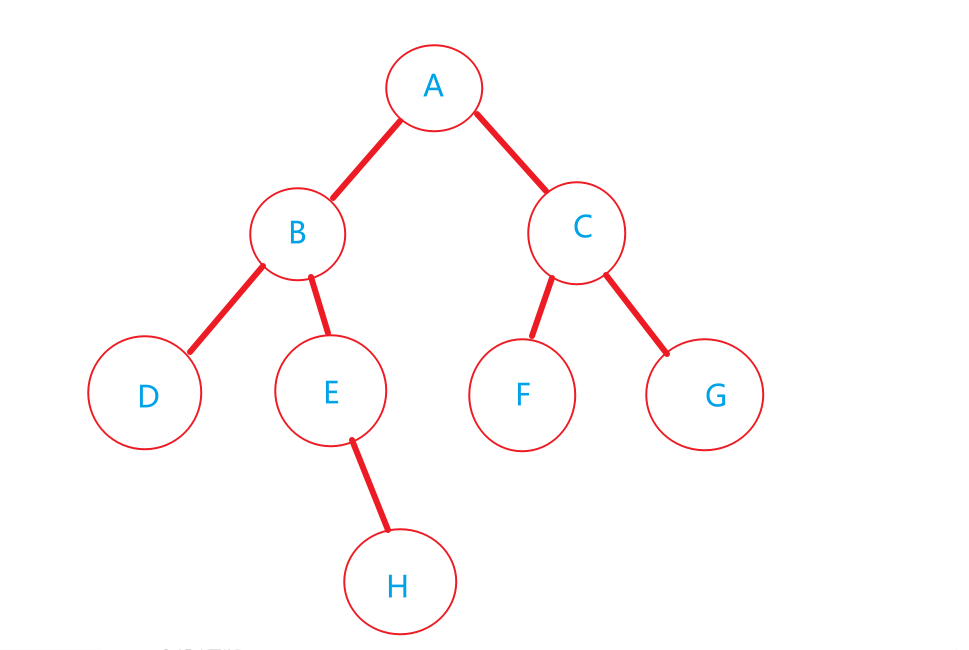
前序遍历
前序遍历(根左右) A B D E H C F G
递归DFS
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
// dfs 深度优先递归
private static void dfs(TreeNode root) {
if(root == null) return;//用于判空,也做为递归出口
list.add(root);//根
dfs(root.left);//左
dfs(root.right);//右
}
迭代(栈)
方式一
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* 迭代法 1 + 栈
* 前序遍历是根左右,首先保存根节点,然后出栈,然后将值入list。
* 然后入右节点、入左节点再重新进行循环,
* 即将左节点当做根节点进行操作(即操作左子树),操作完左子树之后再操作右子树。
*/
private static void iteration1(TreeNode root) {
if (root == null) return;
Deque<TreeNode> stack= new LinkedList<>();
stack.push(root);// 将根节点入栈
while(!stack.isEmpty()){
root = stack.pop();//弹出遍历的节点
list.add(root);
// 先将右子节点入栈,再将左子节点入栈,这样出栈时就会先访问左子节点
if(root.right != null) stack.push(root.right);
if(root.left != null) stack.push(root.left);
}
}
方式二(推荐)
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* 迭代法 2 + 栈
* 入根然后一直入左,直到没有左,然后出栈顶(找到最左的节点),
* 再然后找到最左的节点的右孩子,此时右孩子为根节点。然后循环操作。
* 要点:根节点、左节点处理完之后,把右节点当做根节点然后又从循环开头开始操作(即整理整个右子树)。
*/
private static void iteration(TreeNode root) {
if (root == null) return;
Deque<TreeNode> stack= new LinkedList<>();
while(!stack.isEmpty() || root != null){
while(root != null){ // 左节点一直入栈同时加入到list
list.add(root);
stack.push(root);
root = root.left;
}
root = stack.pop();
root = root.right;//切换右节点继续循环
}
}
中序遍历
中序遍历(左根右) D B E H A F C G
递归DFS
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* dfs 递归 中序遍历
*
*/
private static void dfs(TreeNode root) {
if(root == null) return;
dfs(root.left);
list.add(root);
dfs(root.right);
}
迭代(栈)
方式一
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* 迭代方式一 +栈
*/
private static void iteration(TreeNode root) {
if (root == null) return;
Deque<TreeNode> stack = new LinkedList<>();
while(!stack.isEmpty() || root != null){//注意 栈可能为空 此时root的左子树都遍历完了 继续遍历root.right 所以要加条件root != null
if (root != null) { // 指针来访问节点,访问到最底层
stack.push(root);// 将访问的节点放进栈
root = root.left; // 左
}else {
root = stack.pop();
list.add(root); // 中
root = root.right; // 右
}
}
方式二(推荐)
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* 迭代方式二 +栈
*/
private static void iteration1(TreeNode root) {
if (root == null) return;
Deque<TreeNode> stack = new LinkedList<>();
while(!stack.isEmpty() || root != null) {//注意 栈可能为空 此时root的左子树都遍历完了 继续遍历root.right 所以要加条件root != null
while(root != null){
stack.push(root);
root = root.left;//访问左子树节点到最底层
}
root = stack.pop();//若节点左子树为null 则弹出 加入list
list.add(root);
root = root.right;//接着访问弹出节点的左子树
}
}
后序遍历
后序遍历(左右根) D H E B F G C A
递归DFS
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* dfs 后序递归(左右根) D H E B F G C A
*/
private static void dfs(TreeNode root) {
if(root == null) return;
dfs(root.left);//左
dfs(root.right);//右
list.add(root);//根
}
迭代(栈)
方式一
//全局list集合 //存放树的节点
static List<TreeNode> list = new ArrayList<>();
/**
* 迭代方式一 + 栈 (在前序遍历上改良 交换前序遍历的左右孩子入栈的顺序 得到 根右左 然后再逆转过来就是后序遍历
*/
private static void iteration1(TreeNode root) {
if(root == null) return;
Deque<TreeNode> stack = new LinkedList<>();
stack.push(root);
while(!stack.isEmpty() ){
root = stack.pop();
list.add(root);
if(root.left != null) stack.push(root.left);//相对于前序遍历,这更改一下入栈顺序 使得右节点率先出栈 (根右左--->左右根)
if(root.right != null) stack.push(root.right);
}
//上面得到的其实就是后序遍历的逆序 所以只要把list逆过来就是后序遍历了 (根右左--->左右根)
Collections.reverse(list);
}
方式二(推荐)
/**
* 迭代方式二 + 栈
* 中左一直入栈,直到没有左边,然后查找栈顶节点是否有右节点,没有则出栈入vector,
* 有则将右节点作为根节点重新循环(即将右边那部分直接当做一棵树)。
*/
private static void iteration(TreeNode root) {
if (root == null) {
return ;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode prev = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode peekNode = stack.peek();
if (peekNode.right != null && peekNode.right!= prev) {
// 如果右子节点存在且未被访问过,则处理右子树
root = peekNode.right;
} else {
// 否则,说明左右子树都已经处理完毕,可以访问当前节点
list.add(peekNode);
prev = stack.pop();//记录弹出的节点 用于判断下次处理节点时 右孩子节点是否处理过
}
}
}
层序遍历
层序遍历 A B C D E F G H
迭代(队列)
/**
* 迭代 + 队列
* @param root
*/
private static void iteration(TreeNode root) {
if(root == null) return;
Queue<TreeNode> queue = new LinkedList<>();//队列
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();//记录每层的节点个数
for (int i = 0; i < size; i++) {//取出每层的节点
root = queue.poll();
list.add(root);
if(root.left != null) queue.offer(root.left);//如果当前节点的孩子节点不为空则加入
if(root.right != null) queue.offer(root.right);
}
}
}