写在最前面：

        关于时序分析和约束的学习似乎是学习FPGA的一道分水岭，似乎只有理解了时序约束才能算是真正入门了FPGA，对于FPGA从业者或者未来想要从事FPGA开发的工程师来说，时序约束可以说是一道躲不过去的坎，所以从这篇文章开始，我们来正式进行FPGA时序分析与约束的学习。

        我们在设计FPGA的时候往往是进行多方面性能的权衡来实现设计的最优化，在可实现的情况下，我们一般会期望处理速率越快越好，但是与理论不同，在实际的硬件设计的时候，一个逻辑上正确的设计仍然会因为现实世界中的实现问题而失败！

一、组合电路的时序

1、组合电路的真实时延

        在讨论数字电路层面的时候，我们采用的是一种抽象化模型的方式，这里我们以一个反相器为例：

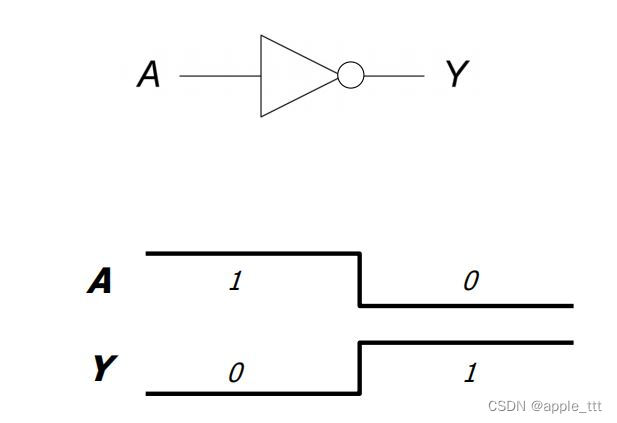
        上图就是一个反相器抽象模型的例子，可以看到，当输入信号A发生变化时，输出信号Y立即发生变化，没有任何时延，这是我们抽象化模型的理想情况。

        但是在真实的硬件电路中，输出会相对于输入有一个时间延迟（晶体管需要变化的时间），如下图：

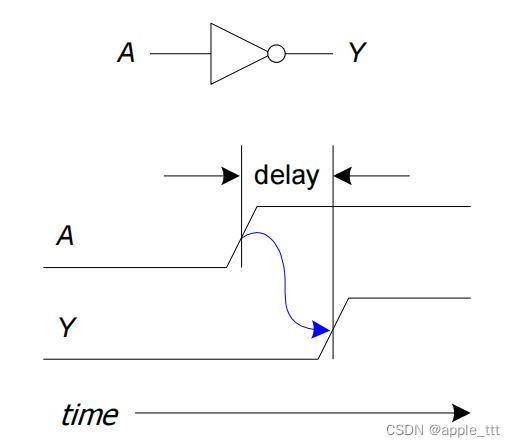
        根据数据测定，一个真实的反相器的延迟情况如下：

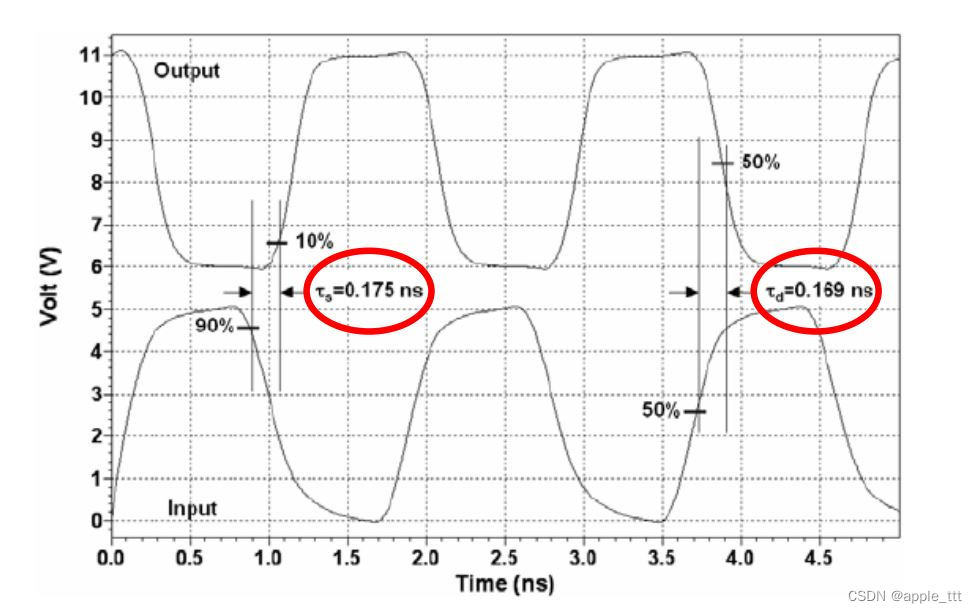
        这样的一个电路延迟根本上来自于：

        （1）在一个电路中的电容和电阻

        （2）光速是有限的（在纳秒尺度上不是那么快，也就不能被认定为无穷大）

        任何影响这些数量的因素都可能改变延迟：

        （1）上升rising（即0 -> 1)与下降falling（即1 -> 0)的输入

        （2）不同的输入有不同的延迟

        （3）环境（如温度等）

        （4）电路老化问题

        我们从输入到输出都有一系列可能的延迟 。

2、从输入到输出Y的时延

        这里首先我们来设定两个基本概念：

Contamination delay (tcd) : 直到输出Y开始变化的时延

Propagation delay     (tpd) : 直到输出Y结束变化的时延

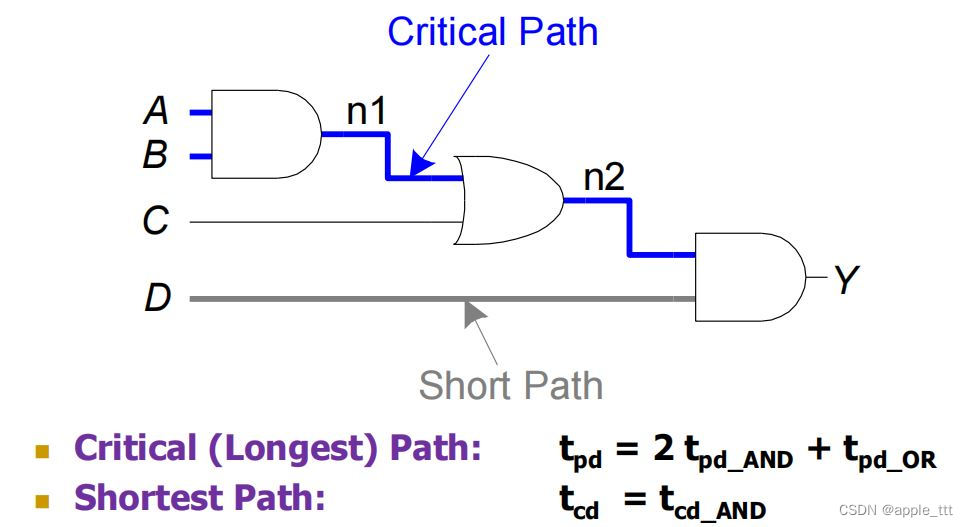
3、组合逻辑时序总结

        真实的组合逻辑电路与我们抽象的数字电路是不一样的，真实的电路在输出相对于输入会有一定的延迟，我们规定了：

• Contamination delay (tcd) : 直到输出Y开始变化的时延，最小的可能时延

        在考虑到输出相对于输入存在时延的情况，那我们就不得不注意毛刺的发生，可以说毛刺对于组合电路的设计来说是一个严峻的挑战。

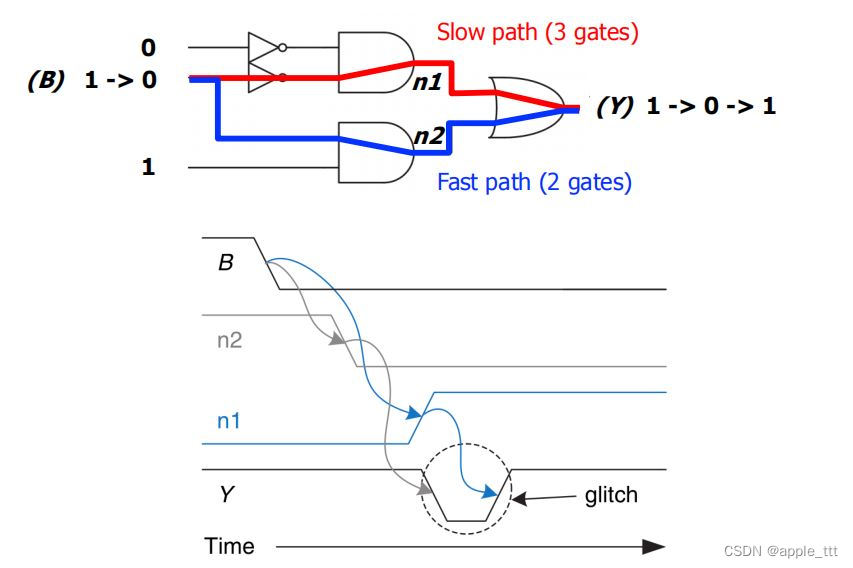
        我们以上图为例， B处数据从1变到0，n2首先发生改变，这个结果通过最快路径先被传递到了输出Y，导致输出变化，等到n1变化的结果通过慢路径被传递到输出Y，结果再次变化，这里就形成了一个毛刺，最终输出Y会呈现一个短暂的0状态。

        我们在数电中学过通过卡诺图的方式来优化电路，消除毛刺，这里不做展开。在这里我们考虑以下问题：我们是不是每次都必须消除毛刺？

        考虑这个问题的原因在于消除毛刺意味着更大的资源和功率消耗，同时也增加了设计者的设计难度，无论有无小故障，该电路最终都能保证收敛到正确的值。

        答案是否定的，我们并不是每一次都需要完全消除毛刺的存在。

        （1）如果说我们只关心长期的稳态输出，我们可以安全地忽略毛刺；

        （2）应该由设计者来决定毛刺在他们自己的应用程序中是否重要。

三、总结

        本文中我们介绍了组合电路的时序问题，定义了tcd和tpd两个重要参数，明确了如何寻找一个组合逻辑电路的最短路径Shortest Path和最长路径Longest Path（更常规的叫法是关键路径Critical Path），然后我们分析了组合逻辑毛刺产生的原因及影响，我们可以通过卡诺图的相关方式来优化电路，消除毛刺，但是这取决于设计者是否需要消除毛刺。

        本文作为时序分析部分的第一篇文章，带领大家初步认识了时序在电路中的存在形式和潜在影响，接下来我们将针对时序逻辑电路的时序问题就行研究。