[递归] 子集 全排列和组合问题

news2024/12/23 4:40:56

1.1 子集I

思路可以简单概括为 二叉树，每一次分叉要么选择一个元素，要么选择空，总共有n次，因此到n+1进行保存结果，返回。像这样：

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int n;
vector<int >temp;
vector<vector<int> > result;
void DFS(int m){
    if (m == n+1){
        result.push_back(temp);
        return ;
    }

    //选择元素m
    temp.push_back(m);
    DFS(m+1);//继续递归
    temp.pop_back();//返回
    //选择空
    DFS(m+1);
}

bool cmp(vector<int > &a,vector<int > &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    
    scanf("%d",&n);
    DFS(1);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;
}

最后自己编写比较函数，简单来说，vector大小相同时，可以直接按照< >这些比较符号进行比较。大小不同时，则按照vector大小进行排序，这里按照题目要求均是小于。

1.2 子集II

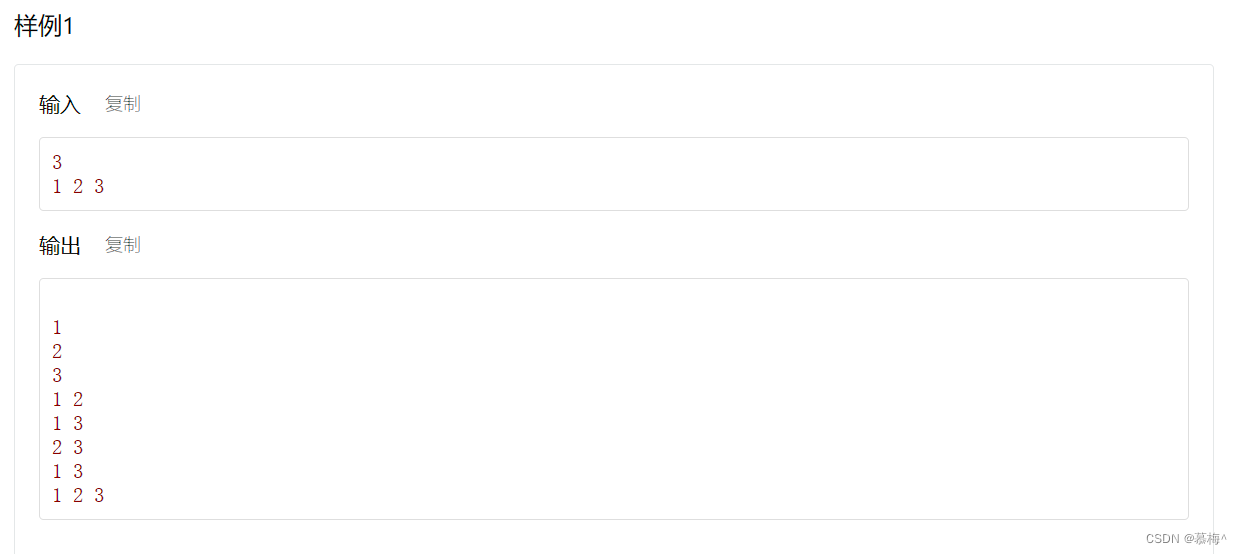
区别在于，自己给定一些元素，进行排序。

那么只需要用一个数组存储这些元素，在压栈/出栈时，换成对应的数组元素即可，思路一致。

代码几乎没有变化。

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
const int N =15;
int q[N];
int n;
void DFS(int m){
    if (m==n+1){
        result.push_back(temp);
        return ;
    }
    temp.push_back(q[m]);
    DFS(m+1);
    temp.pop_back();
    DFS(m+1);
}
bool cmp(vector<int> &a ,vector<int> &b){
    if (a.size()!= b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);
    DFS(1);
    sort(result.begin(),result.end(),cmp);

    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

1.3 子集III

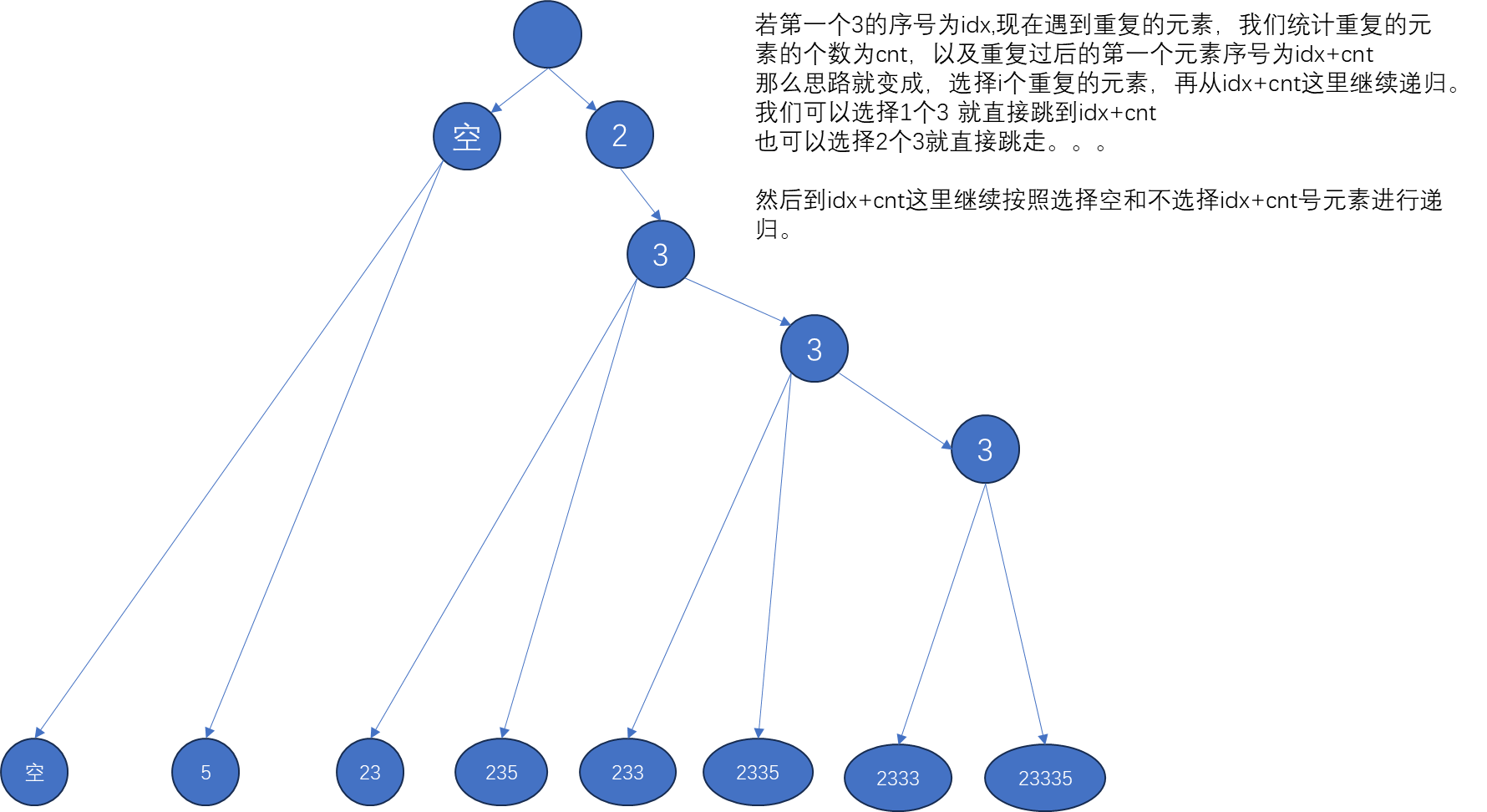
思路还是二叉树深搜递归，但是由于会出现重复的数，按照之前的输出会重复输出一些值，例如样例里的1的子集都会输出两边，因为代码并没有认为第一个1与第二个1是不同的。

首先输入的序列是升序的，因此我们可以连续地处理这些重复的元素。

例如 2 3 3 3 5 

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
const int N =15;
int q[N];
int n;
void DFS(int idx){
    if (idx==n+1){
        result.push_back(temp);
        return ;
    }
    int cnt=1;
    while (idx<n && q[idx]==q[idx+1]){
        cnt++;
        idx++;
    }//经过该循环，idx = 最后一个重复元素的序号，cnt为重复元素的个数

    // 选择空 
    DFS(idx+1);
    //选择重复元素
    for (int i=1;i<=cnt;i++){
        temp.push_back(q[idx]);
        DFS(idx+1);// 选择重复的元素为 1 2 3 ....cnt个
    }
    //在这个循环中，我们将之前添加到 temp 中的元素逐个移除，
    //以回溯到不添加这些重复元素的情况
    for (int i=1;i<=cnt;i++){
        temp.pop_back();
    }
}
bool cmp(vector<int> &a ,vector<int> &b){
    if (a.size()!= b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);
    DFS(1);
    sort(result.begin(),result.end(),cmp);

    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

2.1 全排列I

思路很简单，给个图：

 

设置个q[]表示其是否被使用过，依次递归，返回时再赋值0；

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
int n;
const int N = 10;
int q[N]={0};
void DFS(int m){
    if (m == n+1){
        result.push_back(temp);
    }
    for (int i=1;i<=n;i++){
        if (!q[i]){
            temp.push_back(i);
            q[i]=1;
            DFS(m+1);
            q[i]=0;
            temp.pop_back();
        }

    }

}
bool cmp(vector<int> &a ,vector<int> &b){
    if (a.size()!=a.size())return a.size()<b.size();
    return a<b;
}
int main(){

    scanf("%d",&n);
    DFS(1);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

2.2 全排列II

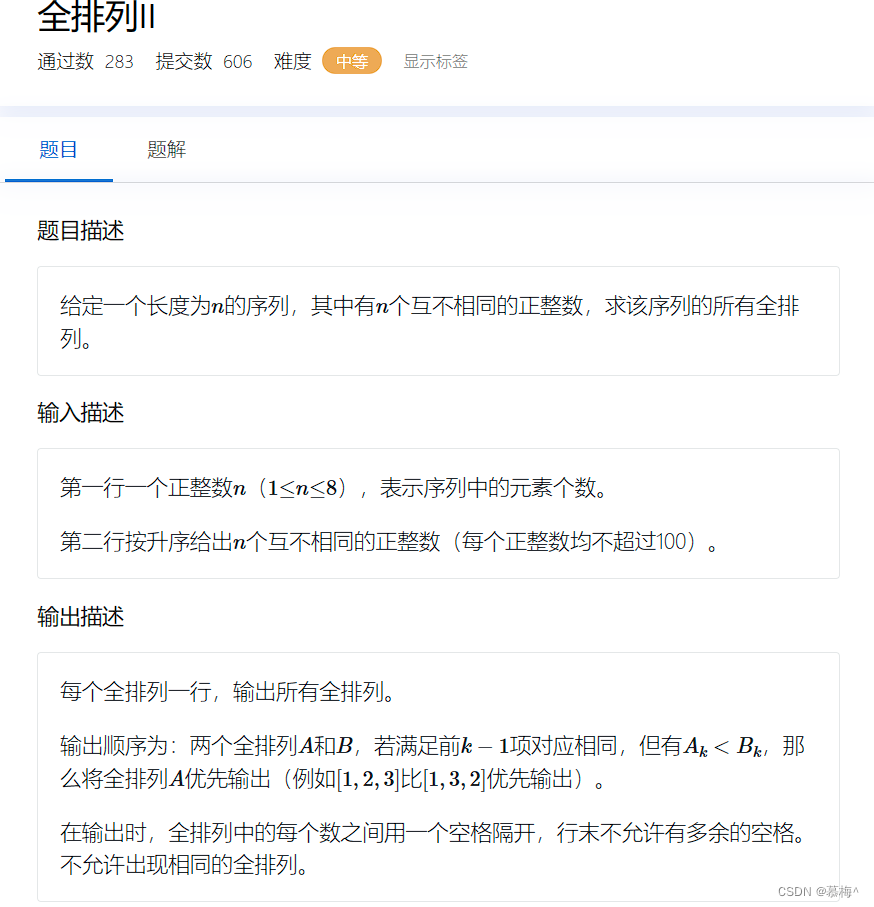
思路依旧简单，全排列I是用i作为正整数，这次是给定正整数压栈和出栈，q[]来储存输入的数，flag[]来表示其是否被使用过，代码相同

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;
int n;
const int N=10;
int q[N];
int flag[N] = {0};
vector<int> temp;
vector<vector<int> > result;
void DFS(int m){
    if (m==n+1){
        result.push_back(temp);
    }
    for (int i=1;i<=n;i++){
        if (!flag[i]){
            temp.push_back(q[i]);
            flag[i]=1;
            DFS(m+1);
            flag[i]=0;
            temp.pop_back();
        }
    }

}
bool cmp(vector<int> &a,vector<int> &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);
    DFS(1);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

2.3 全排列III

如果按照之前的思路，那么样例1会出现大量重复，与子集的解决方法类似，不过是这里是记录每个数的个数，使用cnt[]进行计算，并且每个数只记录一次；

1 1 3 : 只取最后一个重复的id进行记录次数，像这样：cnt[1] = 0 cnt[2]=2 cnt[3] =1

那么全排列就很简单，每次的全排列对于q[i]的数只能用cnt[i]次数。

那么每次for循环

    for (int i=1;i<=n;i++){
        if (cnt[i]){
            temp.push_back(q[i]);
            cnt[i]--;
            DFS(m+1);
            cnt[i]++;
            temp.pop_back();
        }
    }

只能用一次重复的值 

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;
int n;
const int N = 10;
int q[N];
int cnt[N]={0};
vector<int> temp;
vector<vector<int> >result;
void DFS(int m){
    if (m==n+1){
        result.push_back(temp);
        return ;
    }
    for (int i=1;i<=n;i++){
        if (cnt[i]){
            temp.push_back(q[i]);
            cnt[i]--;
            DFS(m+1);
            cnt[i]++;
            temp.pop_back();
        }
    }
}
bool cmp(vector<int> &a,vector<int> &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);
    for (int i=1;i<=n;i++){
        int j=i;
        cnt[i]=1;
        while (j<=n && q[j]==q[j+1]){
            cnt[i]++;
            j++;
        }
        i = j;
    }
    DFS(1);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;


}

3.1 组合I

 

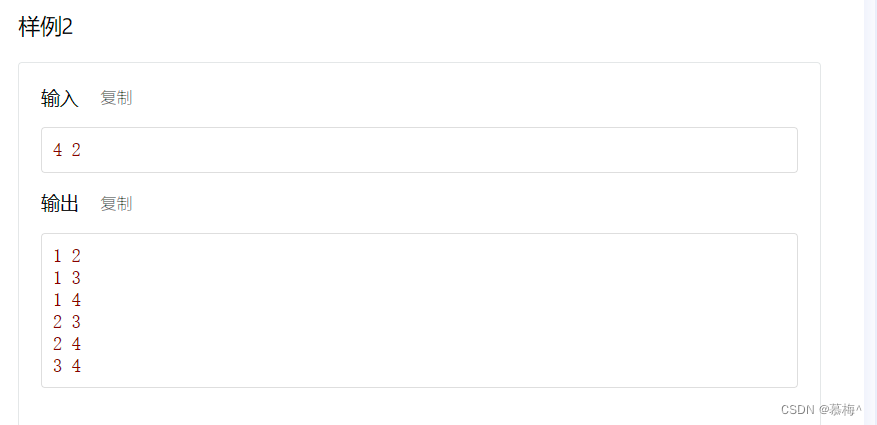
和全排列很像，不过全排列是有顺序的（样例中3 4 和4 3在全排列均是有效的），而组合是无序的，因此我们在挑选的时候可以人为地进行有序限制，从而不会重复。

思路与这道递归题类似

[递归] 自然数分解之方案数_慕梅^的博客-CSDN博客

我们保证后一个数要大于前一个这样的要求，那么就可实现组合题。

样例2中 两个数x y 满足（x<y）

那我们的DFS(int m)，m则是后面的数需要大于的序号

DFS(0)可以作为入口

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;
int n,k;
const int N = 15;


vector<int> temp;
vector<vector<int> > result;

void DFS(int m){
    if (temp.size()==k){//递归的出口则改为vector <int> temp的大小==k
        result.push_back(temp);
        return ;
    }
    for (int i=m+1;i<=n;i++){
        //循环从 序号m+1开始
        temp.push_back(i);
        DFS(i);//将i作为参数进行下一次的递归
        temp.pop_back();
    }
    return ;

}
bool cmp(vector<int> &a,vector<int> &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    scanf("%d%d",&n,&k);
    DFS(0);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

 3.2 组合II 

需要自己输入序列，思路不变

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;
int n,k;
const int N = 15;
int q[N];
vector<int> temp;
vector<vector<int> > result;

void DFS(int m){
    if (temp.size()==k){
        result.push_back(temp);
        return ;
    }
    for (int i=m+1;i<=n;i++){
        temp.push_back(q[i]);
        DFS(i);
        temp.pop_back();
    }
}
bool cmp(vector<int> &a,vector<int> &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);

    DFS(0);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

3.3 组合III

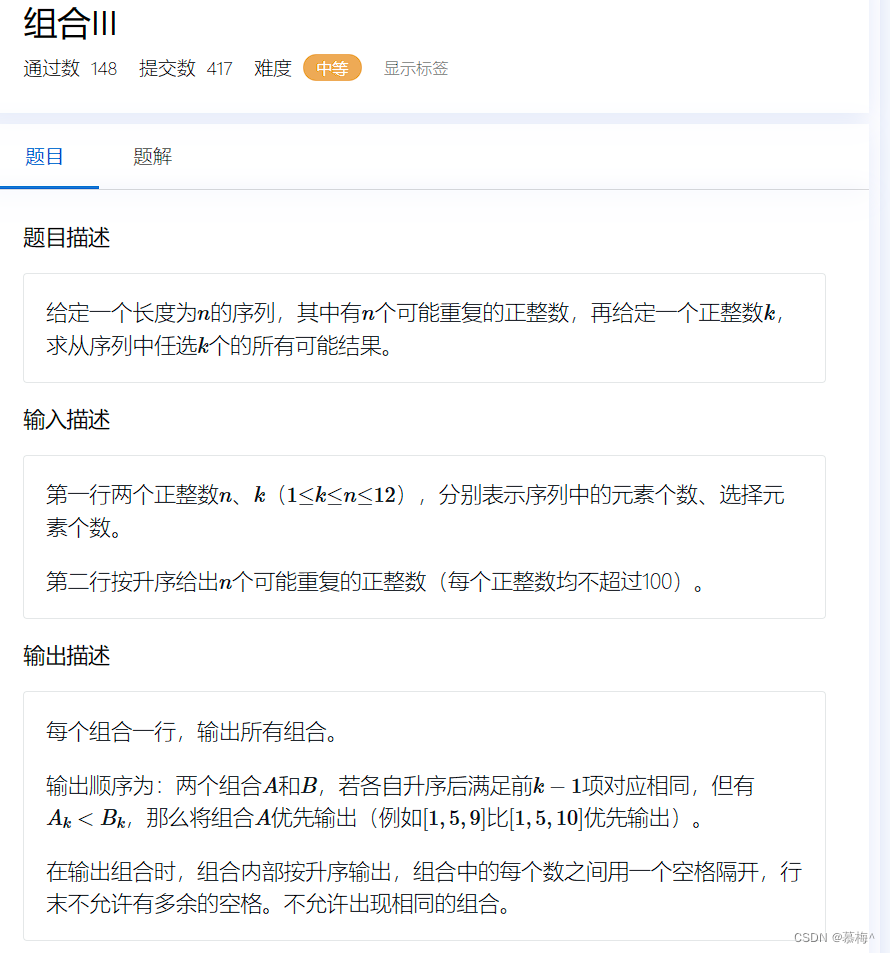
 可以借鉴全排列的思想，使用cnt来进行计数

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;
int n,k;
const int N = 15;
int q[N];
int cnt[N]={0};
vector<int> temp;
vector<vector<int> > result;

void DFS(int m){
    if (temp.size()==k){
        result.push_back(temp);
        return ;
    }
    for (int i=m;i<=n;i++){//i从m开始，因为有重复的元素。
        if (cnt[i]){
            cnt[i]--;
            temp.push_back(q[i]);
            DFS(i);
            cnt[i]++;
            temp.pop_back();
        }
    }
}
bool cmp(vector<int> &a,vector<int> &b){
    if (a.size()!=b.size())return a.size()<b.size();
    return a<b;
}
int main(){
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++)scanf("%d",&q[i]);
    for (int i=1;i<=n;i++){
        int j = i;
        cnt[i] = 1;
        while ((j+1)<=n&&q[j]==q[j+1]){
            cnt[i]++;
            j++;
        }
        i = j;
    }

    DFS(0);
    sort(result.begin(),result.end(),cmp);
    for (int i=0;i<result.size();i++){
        for (int j=0;j<result[i].size();j++){
            if (j==result[i].size()-1)printf("%d",result[i][j]);
            else printf("%d ",result[i][j]);
        }
        printf("\n");
    }
    return 0;

}

不过与前两个组合不同的是

for (int i=m+1;i<=n;i++){

条件因改为

for (int i=m;i<=n;i++){

 如果不该与，之前的序列都是没有重复的元素，因此可以下一次的序号需要+1以保证大于前面的数，然而这里有重复的元素，因此从m开始。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/957503.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[ros][ubuntu]ros在ubuntu18.04上工作空间创建和发布一个话题

[ros][ubuntu]ros在ubuntu18.04上工作空间创建和发布一个话题

构建catkin工作空间 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src catkin_init_workspace cd ~/catkin_ws/ catkin_make 配置环境变量 echo "source ~/catkin_ws/devel/setup.bash" >> ~/.bashrc source ~/.bashrc 检查环境变量 echo $ROS_PACKAGE_PATH…
阅读更多...
学习笔记-ThreadLocal

学习笔记-ThreadLocal

ThreadLocal 什么是ThreadLocal&#xff1f; ThreadLocal 是线程本地变量类&#xff0c;在多线程并行执行过程中&#xff0c;将变量存储在ThreadLocal中&#xff0c;每个线程中都有独立的变量&#xff0c;因此不会出现线程安全问题。 应用举例 解决线程安全问题&#xff1a;例…
阅读更多...
pytest---添加自定义命令行参数（pytest_addoption ）

pytest---添加自定义命令行参数（pytest_addoption ）

前言 在目前互联网公司中&#xff0c;都会存在多个测试环境&#xff0c;那么当我们编写的自动化想要在多套测试环境下进行运行时&#xff0c;如何使用&#xff1f;大多数人想到的可能是通过将我们自动化代码中的地址修改成不同环境&#xff0c;但是这时候就会增加一些工作量&am…
阅读更多...
Java设计模式：四、行为型模式-07：状态模式

Java设计模式：四、行为型模式-07：状态模式

文章目录 一、定义&#xff1a;状态模式二、模拟场景&#xff1a;状态模式2.1 状态模式2.2 引入依赖2.3 工程结构2.4 模拟审核状态流转2.4.1 活动状态枚举2.4.2 活动信息类2.4.3 活动服务接口2.4.4 返回结果类 三、违背方案&#xff1a;状态模式3.0 引入依赖3.1 工程结构3.2 活…
阅读更多...
JVM的故事——垃圾收集器

JVM的故事——垃圾收集器

垃圾收集器 文章目录 垃圾收集器一、serial收集器二、parnew收集器三、parallel scavenge收集器四、serial old收集器五、parallel old收集器六、CMS收集器七、Garbage First收集器八、收集器的权衡 一、serial收集器 新生代收集器&#xff0c;最基础的收集器&#xff0c;单线…
阅读更多...
C#备份数据库文件

C#备份数据库文件

c#备份数据库文件完整代码 sqlServer 存储过程&#xff1a; USE [PSIDBase] GO /****** Object: StoredProcedure [dbo].[sp_BackupDB] Script Date: 2023/8/31 16:49:02 ******/ SET ANSI_NULLS ON GO SET QUOTED_IDENTIFIER ON GOALTER procedure [dbo].[sp_BackupDB]…
阅读更多...
【Unity每日一记】WheelColider组件汽车游戏的关键

【Unity每日一记】WheelColider组件汽车游戏的关键

&#x1f468;‍&#x1f4bb;个人主页&#xff1a;元宇宙-秩沅 &#x1f468;‍&#x1f4bb; hallo 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! &#x1f468;‍&#x1f4bb; 本文由 秩沅 原创 &#x1f468;‍&#x1f4bb; 收录于专栏&#xff1a;uni…
阅读更多...
2023年腾讯云优惠券(代金券)领取方法整理汇总

2023年腾讯云优惠券(代金券)领取方法整理汇总

腾讯云优惠券是腾讯云为了吸引用户而推出的一种优惠凭证&#xff0c;领券之后新购、续费、升级腾讯云的相关产品可以享受优惠&#xff0c;从而节省一点的费用&#xff0c;下面给大家分享腾讯云优惠券领取的几种方法。 一、腾讯云官网领券页面领取 腾讯云官网经常推出各种优惠活…
阅读更多...
C#，数值计算——Midinf的计算方法与源程序

C#，数值计算——Midinf的计算方法与源程序

1 文本格式 using System; namespace Legalsoft.Truffer { public class Midinf : Midpnt { public new double func(double x) { return funk.funk(1.0 / x) / (x * x); } public Midinf(UniVarRealValueFun funcc, double aa,…
阅读更多...
内存四区(个人学习笔记黑马学习)

内存四区(个人学习笔记黑马学习)

1、内存分区模型 C程序在执行时&#xff0c;将内存大方向划分为4个区域&#xff1a; 代码区:存放函数体的二进制代码&#xff0c;由操作系统进行管理的全局区:存放全局变量和静态变量以及常量栈区:编译器自动分配释放,存放函数的参数值,局部变量等 堆区:由程序员分配和释放,若程…
阅读更多...
SpringBoot整合Freemaker结合Vue实现页面填写一键自动生成Redis的配置文件

SpringBoot整合Freemaker结合Vue实现页面填写一键自动生成Redis的配置文件

&#x1f9d1;‍&#x1f4bb;作者名称&#xff1a;DaenCode &#x1f3a4;作者简介&#xff1a;啥技术都喜欢捣鼓捣鼓&#xff0c;喜欢分享技术、经验、生活。 &#x1f60e;人生感悟&#xff1a;尝尽人生百味&#xff0c;方知世间冷暖。 &#x1f4d6;所属专栏&#xff1a;Sp…
阅读更多...
DCMM数据能力成熟度评估模型--学习笔记

DCMM数据能力成熟度评估模型--学习笔记

DCMM数据能力成熟度评估模型--学习笔记 1、DCMM简介、结构组成和成熟度评估等级划分1.1 DCMM简介1.2 DCMM结构组成1.3 DCMM关键过程域1.3.1、数据战略&#xff08;指导方针&#xff09;1.3.2、数据治理 &#xff08;机制保障&#xff09;1.3.3、数据架构 (施工图纸)1.3.4、数据…
阅读更多...
WebRTC-Streamer交叉编译

WebRTC-Streamer交叉编译

WebRTC-Streamer交叉编译 flyfish 文章目录 WebRTC-Streamer交叉编译零、前言一、提前准备工作1 安装需要的工具2 可选的交叉编译工具3 默认执行python是python34 获取源码5 使用其他版本的方法 二、非交叉编译编译1 在 src目录执行 安装所需的依赖2 执行命令 三、 交叉编译1 …
阅读更多...
【GAMES202】Real-Time Global Illumination(in 3D)—实时全局光照(3D空间)

【GAMES202】Real-Time Global Illumination(in 3D)—实时全局光照(3D空间)

一、SH for Glossy transport 1.Diffuse PRT回顾 上篇我们介绍了PRT&#xff0c;并以Diffuse的BRDF作为例子分析了预计算的部分&#xff0c;包括Lighting和Light transport&#xff0c;如上图所示。 包括我们还提到了SH&#xff0c;可以用SH的有限阶近似拟合球面函数&#xff…
阅读更多...
【进阶篇】MySQL的SQL解析原理详解

【进阶篇】MySQL的SQL解析原理详解

文章目录 0. 前言1. SQL解析过程1. 词法分析2. 语法分析4. 语法分析树5. MySQL语法分析树生成过程6. 核心数据结构及其关系7. SQL解析的应用 2. 参考文档 0. 前言 你是否已经深入了解了MySQL中 SQL解析过程&#xff0c;以及解析过程中每个环节扮演的具体角色&#xff1f;你是否…
阅读更多...
Windows SQLYog连接不上VMbox Ubuntu2204 的Mysql解决方法

Windows SQLYog连接不上VMbox Ubuntu2204 的Mysql解决方法

Windows SQLYog连接不上VMbox Ubuntu2204 的Mysql解决方法 解决方法&#xff1a; 1、先检查以下mysql的端口状态 netstat -anp|grep mysql如果显示127.0.0.1:3306 则说明需要修改&#xff0c;若为: : :3306&#xff0c;则不用。 在**/etc/mysql/mysql.conf.d/mysqld.cnf**&am…
阅读更多...
软件测试之黑盒测试、白盒测试分别是什么?有什么区别?

软件测试之黑盒测试、白盒测试分别是什么?有什么区别?

软件开发过程中&#xff0c;为了保证软件质量和稳定性&#xff0c;必须进行全面而细致的测试工作&#xff0c;而黑盒测试和白盒测试正是两种常用的测试方法。 一、黑盒测试 黑盒测试是一种基于软件外部功能的测试方法。测试人员对待测试的软件系统&#xff0c;就像一个黑匣子…
阅读更多...
uniapp-秋云图表 ucharts echarts 对比与关系

uniapp-秋云图表 ucharts echarts 对比与关系

科普&#xff1a; 秋云图表库&#xff0c;包含二种配置属性对应二种js配置文件。 一种是 &#xff1a;echarts.js,一种是 &#xff1a; ucharts。 二者的配置属性不一样&#xff01; ucharts和echarts对比 ucharts和echarts都是用于数据可视化的开源JavaScript库&#xff0c;它…
阅读更多...
【高危】Apache Airflow Spark Provider 反序列化漏洞 (CVE-2023-40195)

【高危】Apache Airflow Spark Provider 反序列化漏洞 (CVE-2023-40195)

zhi.oscs1024.com​​​​​ 漏洞类型反序列化发现时间2023-08-29漏洞等级高危MPS编号MPS-qkdx-17bcCVE编号CVE-2023-40195漏洞影响广度广 漏洞危害 OSCS 描述Apache Airflow Spark Provider是Apache Airflow项目的一个插件&#xff0c;用于在Airflow中管理和调度Apache Spar…
阅读更多...
自动化机器学习Auto-Sklearn安装和使用教程

自动化机器学习Auto-Sklearn安装和使用教程

安装和使用 Auto-Sklearn Auto-sklearn 提供了开箱即用的监督型自动机器学习。从名字可以看出，auto-sklearn 是基于机器学习库 scikit-learn 构建的，可为新的数据集自动搜索学习算法，并优化其超参数。因此，它将机器学习使用者从繁琐的任务中解放出来，使其有更多时间专注于…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023