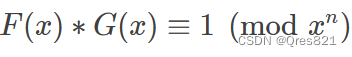
已知
F
F
F,求
G
G
G
考虑倍增
F
(
x
)
∗
H
(
x
)
≡
1
(
m
o
d
x
n
/
2
)
F(x) * H(x) \equiv 1 \pmod{x^{n/2}}
F(x)∗H(x)≡1(modxn/2)
F ( x ) ∗ G ( x ) ≡ 1 ( m o d x n / 2 ) F(x) * G(x) \equiv 1 \pmod{x^{n/2}} F(x)∗G(x)≡1(modxn/2)
假设 H H H 已知,求G
做差可得: H − G ≡ 0 ( x n / 2 ) H-G\equiv 0(x^{n/2}) H−G≡0(xn/2)
因为要变成 x n x^n xn,所以两边平方
对于 H 2 − 2 H G + G 2 H^2-2HG+G^2 H2−2HG+G2 化简,直接乘 F F F
最后可以推出: G = 2 H − F H 2 G=2H-FH^2 G=2H−FH2,递归然后NTT即可
void Inv(int *F, int *G, int n) {
if(n==1) {
G[0]=pw(F[0], mo-2); //只有一项直接取逆元
return ;
}
Inv(F, G, (n+1)>>1);
m=n; l=0;
for(n=1; n<(m<<1); n<<=1) ++l; //建议弄到2*m
for(i=0; i<n; ++i) r[i]=((r[i>>1]>>1) | ((i&1)<<l-1));
for(i=0; i<m; ++i) c[i]=F[i];
for(i=m; i<n; ++i) c[i]=0; //记得清0
NTT(c, 1, n); NTT(G, 1, n);
for(i=0; i<n; ++i) G[i]=Mod(2*G[i]%mo-c[i]*G[i]%mo*G[i]%mo);
NTT(G, -1, n);
for(i=m; i<n; ++i) G[i]=0; //记得清0
}
注:
对于 n = 5 n=5 n=5 的多项式完全输出应该是这样的: